人工神经网络模型——多层感知器及其他

本教程解释了人工神经网络模型——多层感知器、反向传播、径向偏差和 Kohonen 自组织地图，包括它们的架构：

在上一篇关于神经网络学习规则的教程中，我们通过示例学习了 Hebbian 学习和感知器学习算法。

人工神经网络多层感知器：在监督学习中，神经网络知道期望的输出，通常称为网络的目标值。它优化其性能以减少实际输出和目标之间的误差。

另一方面，无监督类型的学习没有关于目标值的任何信息。它试图通过形成集群来识别输入中隐藏的模式趋势，从而自行优化其性能。

梯度下降和随机学习算法属于监督学习算法的范畴。Hebbian和 Competitive 学习算法属于无监督学习算法的范畴。我们在之前的教程中研究了这些。

你会学到什么：

• 机器学习和人工神经网络模型
  • 什么是多层感知器？
  • 反向传播网络
    • 使用 BP 算法最小化误差
    • BP 网络架构
    • 反向传播算法的训练过程
    • 影响反向传播网络的因素
  • 径向偏置函数
    • 径向偏置函数的架构
    • 径向偏置函数的训练
  • Kohonen 自组织特征图
    • Kohonen 自组织特征图的架构
    • 特征图的训练
• 结论

机器学习和人工神经网络模型

让我们快速浏览一下人工神经网络的结构。

ANN有3层，即输入层、隐藏层和输出层。每个 ANN 都有一个输入和输出，但也可能没有、一个或多个隐藏层。ANN 的结构分为多种类型的架构，例如单层、多层、前馈和循环网络。

人工神经网络中的每个输入神经元都有相关的权重，偏差也带有权重。激活函数应用于净输入以计算输出。然后将输出与目标进行比较并调整权重。

激活函数有多种类型，例如二元阶跃函数、双极阶跃函数、Sigmoidal 函数等。

上述术语如下图所示：

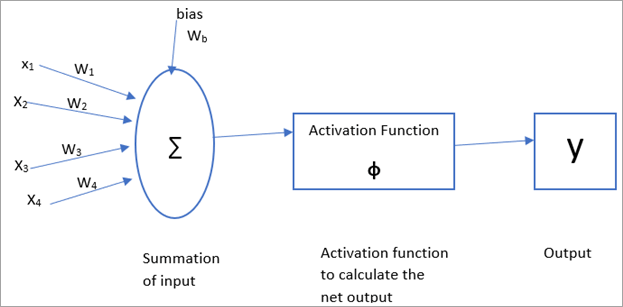
在本教程中，我们将重点介绍人工神经网络模型——多感知器、径向偏差和 Kohonen 自组织映射。

什么是多层感知器？

具有一个或多个隐藏层的感知器网络称为多层感知器网络。多感知器网络也是前馈网络。它由单个输入层、一个或多个隐藏层和单个输出层组成。

由于增加了层数，MLP 网络扩展了简单感知器网络的有限信息处理的局限性，并且在逼近能力上具有高度的灵活性。训练 MLP 网络并使用反向传播学习方法更新权重，下面将详细解释。

使用单层感知器无法解决的简单感知器网络的一些限制，例如 XOR 问题，可以使用 MLP 网络来解决。

多层感知器工作原理：反向传播网络

反向传播 (BP) 网络是前馈多层感知器网络的一种应用，每一层都具有可微的激活函数。

对于给定的训练集，反向传播网络中层的权重由激活函数调整以对输入模式进行分类。BPN 中权重更新的发生方式与梯度下降法应用于单个感知器网络的方式相同。

使用 BP 算法最小化误差

在这个算法中，实际输出和目标之间的误差被传播回隐藏单元。为了最小化误差，更新权重。为了更新权重，在输出层计算误差。

为了进一步最小化误差并计算隐藏层的误差，应用了一些有助于计算和减少隐藏层误差的先进技术，从而获得更准确的输出。

隐藏层数越多，网络变得越复杂，速度越慢，但更有利。该系统也可以用一个隐藏层进行训练。一旦经过训练，它将开始快速产生输出。

这种学习算法称为反向传播学习，网络称为反向传播网络。

反向传播学习分 3 个阶段完成：

1. 输入训练模式是前馈的。
2. 计算实际输出和目标值之间的误差。
3. 权重更新。

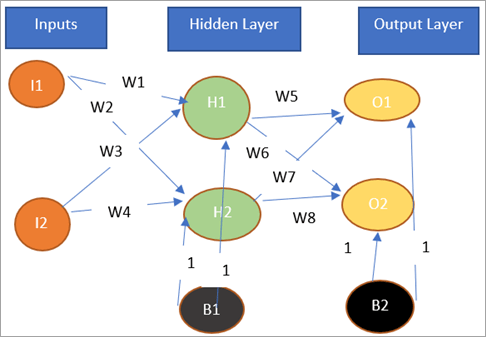
人工神经网络多层感知器：BP 网络架构

让我们看看反向传播网络的架构。

反向传播网络是一个前馈多层网络。它有一个输入层、一个隐藏层和一个输出层。偏置被添加到网络的隐藏层和输出层，激活函数=1。BPN 的输入和输出可以是二进制 (0,1) 或双极 (-1,+1)。

激活函数是可微的、单调的和增量的，通常在二元 sigmoidal 或双极 sigmoidal 之间选择。

反向传播网络具有前馈阶段，其中数据从输入向输出馈送，以及反向传播阶段，其中信号以相反方向发回以最小化误差。

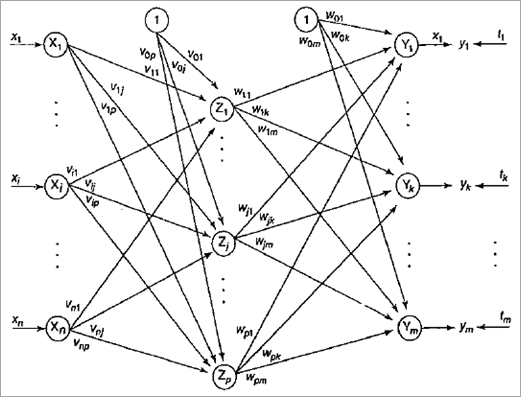
人工神经网络模型原理：反向传播算法的训练过程

从上图中，

Step1：初始化随机权重和学习率。

Step2：输入单元接收x _i作为输入，发送给隐藏单元。

步骤 3：隐藏层单元 z _j的净输入计算为

Step 4:隐藏层的Net Output计算为z _j = f (z _input )，激活函数取二元或双极Sigmoidal。

步骤 5：输出层的净输入计算为z _j = f (z _input )。

Step 6：输出层的净输出：f(y _input )，激活函数取二元或双极sigmoidal。

第 7 步：计算  其中输出单元 y _k (k=1 to m) 接收输入训练模式对应的目标模式。

找出函数的导数。

第 8 步：纠错和权重更新。

重量更新：

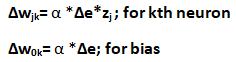
错误向后发送。

步骤 9：更新输出单元：(y _k , k=1 to m) 更新偏差和权重：

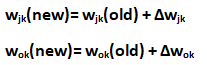
第 10 步：检查作为完成的 epoch 数给出的停止条件。

重复步骤2～9，直到得到停止条件。

人工神经网络模型介绍：影响反向传播网络的因素

影响反向传播网络训练的一些因素是：

1. 初始权重：选择的初始随机权重非常小，因为二进制 sigmoidal 函数中的较大输入可能会导致一开始就饱和，从而导致函数卡在局部最小值处。一些初始化权重的方法可以使用 Nguyen-Widow 的初始化。它通过提高隐藏单元的学习能力来分析隐藏神经元对单个输入的响应。这导致 BPN 更快收敛。
2. 学习率：学习率的一个大值，有助于更快的收敛，但可能会导致过冲。范围 从 10 ^-3到 10 用于各种 BPN 实验。
3. 训练数据的数量：输入训练数据应该覆盖整个输入空间，输入集的集合应该随机选择。
4. 隐藏层节点的数量：选择隐藏层节点的数量以实现网络的最佳性能。对于没有收敛到一个解的网络，可以选择更多的隐藏节点，而对于快速收敛的网络，选择很少的隐藏层节点。

反向传播网络示例

对于下面的网络图，让我们用给定的数字计算新的权重：

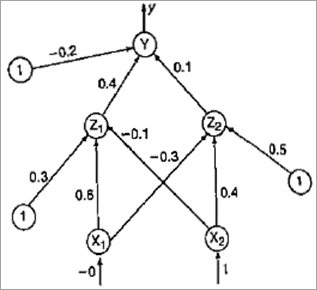
输入向量 = [0,1]
目标输出 = 1
学习率 = 0.25
激活函数 = 二元 sigmoidal 激活函数

解决方案：

从上图中我们可以看到 Z ₁的输入向量： [v ₁₁ , v ₂₁ , v ₀₁ ] 是 [ 0.6, -0.1, 0.3]
Z _{2 的}输入向量_： [v ₁₂ , v ₂₂ , v ₀₂ ] = [-0.3, 0.3, 0.5]
Y 的输入向量： [w ₁ , w ₂ , w ₀ ] = [ 0.4, 0.1, -0.2]
激活函数由 f(x)= 1/ (1 +e ^{- x} )
输入 x= [0,1] 和目标 t=1

步骤 1： 计算 Z ₁的净输入权重

Z _in1 =v ₀₁ + x _{1 *} v ₁₁ + x ₂ * v ₂₁

• 0.3 + 0* 0.6 +1 *0.1
• 0.2

Z _in2 = v ₀₂ + x _{1 *} v ₂₁ + x ₂ * v ₂₂

• 0.5+ 0*0.6 +1*(0.4)
• 0.9

步骤 2：应用激活函数

z _i = f(Z _in1 ) = 1/1+e ^-z _in1

• 1/1+e ^-0.2
• 0.5498

z _j = f(Z _in2 ) = 1/1+e ^-z _in2

• 1/1+e ^-0.9
• 0.7109

第三步：计算输出层的净输入

y _in = w ₀ + z _i *w ₁ + z _j *w ₂

= -0.2+ 0.5498 * 0.4 + 0.7109 *0.1
= 0.09101

步骤 4： 使用激活计算净输出

y= f(y _in ) = 1/1+e ^-y _in

• 1/1+e ^-0.09101
• 0.5227

第 5 步：计算误差

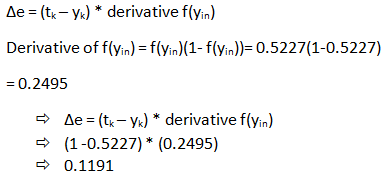
第 6 步：权重更新

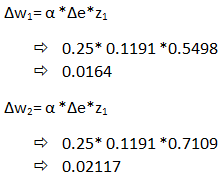
第 7 步：新的权重计算

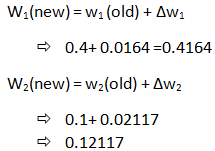
因此，最终权重计算为 W ₁ (new)= 0.4164, W ₂ (new) =0.12117

*假设：输入和隐藏层向量之间的误差取为0。

径向偏置函数

径向偏置函数由 MJD Powell 开发。它是一种分类和逼近算法。高斯函数是在径向偏置网络中使用的非线性函数。高斯函数用于网络的正则化。

它被定义为：

f(y)= e ^{-y^2}，对于所有 y 值，f(y) 始终为正，f(y) 随着 |y| 减少 0 接近0。

f(y) = -2 *y * f(y) 的导数

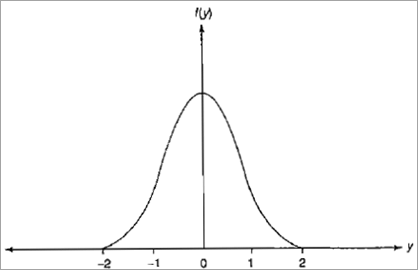
径向偏差这个名称来自这样一个概念，即该函数为距内核中心固定径向距离的输入提供相同的输出。这些输入是径向对称的，因此称为径向偏置函数网络。

径向偏置函数的架构

径向偏置函数的架构如下所示。

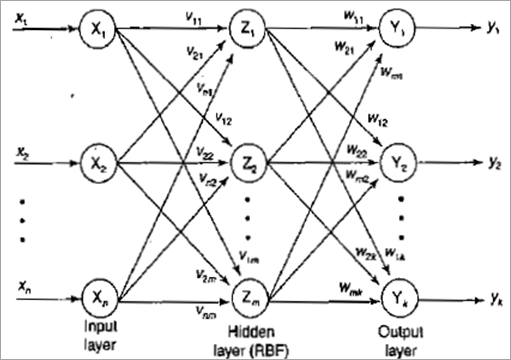
径向偏置函数网络由输入层、隐藏层和输出层组成。

隐藏层节点是径向偏置函数 (RBF) 节点。隐藏层具有非线性基函数，可对输入刺激产生响应。输入应该在输入空间的局部区域之下。因此，该网络也称为局部感受野网络。

径向偏置函数的训练

步骤 1：将权重设置为一些随机初始值。

第二步：每个输入节点接收输入信号。

输入单位： x _i代表所有 I = 1 到 n

步骤 3：使用高斯函数计算径向偏置函数。

步骤 4：从输入向量中选择足够数量的中心。

步骤 5：隐藏单元的输出计算为

其中 x^ _ji是输入向量的径向偏置函数单元的中心， 是第 i 个 RBF 单位的宽度，x _ji是输入向量模式的第 j 个变量。

第 6 步：输出计算如下：

在哪里，

k 是隐藏层节点的数量。
y _net是第 n 个传入模式的输出层中第 m 个节点的输出值。
w _o是第 n 个输出节点的偏置项。

步骤 7：计算误差并检查停止条件，例如 epoch 数等。

人工神经网络多层感知器：Kohonen 自组织特征图

Feature Maps 是一种将多维输入转换为一维或二维数组的方法，即将庞大的数组空间转换为特征空间，同时保持输入特征的属性。

要获得特征图，是否需要识别一维或二维数组。这些一维或二维神经阵列被称为自组织神经阵列。它是一个无监督的学习网络。

例如，有一维或二维阵列排列的 m 个单元的输出簇和 n 个单元的输入信号。给定的输出模式作为输入模式的参考。因此，当自组织完成时，与权重向量簇单元紧密匹配的输入向量单元被选为获胜者。

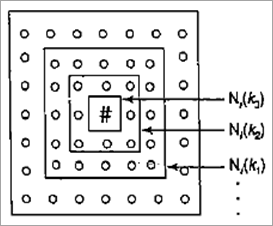
为了找到最近的输入单元，使用欧几里德距离公式计算权重向量。

因此，对于具有最小平方（欧几里德距离）的单元，选择输入单元作为获胜者。另一种找到获胜输入神经元的方法是使用点积。具有最大点积的单元被选为获胜者。

集群的矩形网格如上所示。N(k ₁ )、N(k ₂ )、N(k ₃ ) 是半径，其中k ₁ >k ₂ >k _3。获胜单元用“#”表示，其他输出单元用“o”表示. 每个单元有八个最近的邻居。

人工神经网络模型介绍：Kohonen 自组织特征图的架构

Kohonen 自组织映射的架构如下所示：

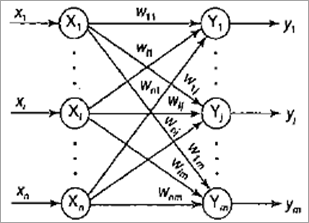
有2层，即输入层和输出层。输入层由 n 个单元组成，输出层由 m 个单元组成。

权重更新发生在使用欧几里德距离或点积方法计算的获胜神经元单元上。网络会一直训练到找到 epoch 数或学习率降低到一个非常小的值。

特征图的训练

步骤 1：初始化随机权重 w _ij和学习率. 可以选择它作为输入值的样本范围。

步骤 2：计算每个输入向量 x 的欧几里得距离的平方。

第 3 步：获胜单位将是 D(j) 最小值的单位。

第 4 步：权重更新和新权重的计算。

第 5 步：更新学习率

步骤6：以特定间隔减小拓扑邻域的半径。

步骤7：重复步骤2-6，直到接收到停止条件。

人工神经网络模型原理：Kohonen 自组织映射示例

对于给定的输入向量，构造一个 Kohonen 自组织映射

有四个给定的向量：[0 0 1 1]、[1 0 0 0]、[0 1 1 0]、[ 0 0 0 1]。
形成2个集群。
初始学习率：0.5

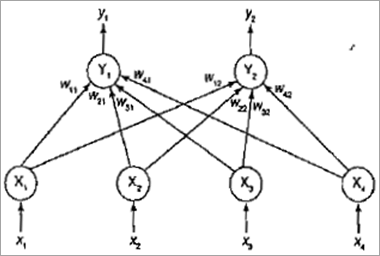
步骤 1：初始化 0 和 1 之间的权重。

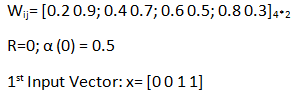
第 2 步：计算欧几里得距离：

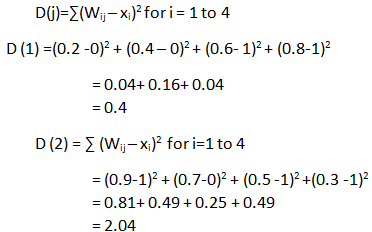
由于 D(1)<D(2) 因此 D(1) 是最小值。因此，获胜的集群单元是 Y1。

第 3 步：更新获胜集群单元的权重。

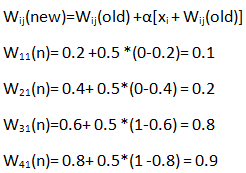
更新后的权重矩阵
W _ij = [0.1 0.9; 0.2 0.7; 0.8 0.5; 0.9 0.3]

类似地，计算其他三个输入的新权重矩阵。

对于^第二个输入：
W _ij =[0.1 0.95;0.2 0.35; 0.8 0.25; 0.9 0.15]

对于^第三个输入：
W _ij = [0.05 0.95; 0.6 0.35;0.9 0.25; 0.45 0.15]

对于^第4^个输入：
W _ij = [0.025 0.95; 0.3 0.35; 0.45 0.25; 0.475 0.15]

第^一次迭代或纪元已完成。

第 4 步：更新学习率。

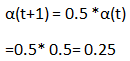
更新重量图

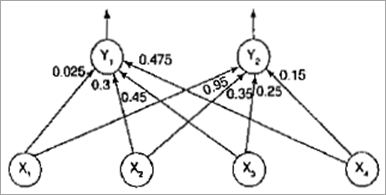
可以执行更多的迭代，直到学习率降低到非常小的值或直到半径变为零。

人工神经网络多层感知器结论

人工神经网络模型介绍：多层感知器网络是具有一个或多个隐藏层的网络。反向传播网络是一种具有 2 个阶段的 MLP，即前馈阶段和反向阶段。

多层感知器工作原理：在前馈阶段，输入神经元模式被馈送到网络，并在输入信号通过隐藏的输入和输出层时计算输出。

在反向阶段，误差被反向传播到隐藏层和输入层以进行权重调整。当实际输出与目标值进行比较时，在输出层计算误差。

一些网络还会计算隐藏层的误差，并将其传播回输入层。这有助于提高准确性和收敛性。BPN 是受监督的多层感知器网络。

径向偏置函数使用高斯或 Sigmoidal 函数来正则化网络。对于许多输入节点，每个节点在距内核中心的固定径向距离内产生相似的输出。

Kohonen 自组织映射是无监督学习算法，可将多维输入空间向量转换为一维或二维空间向量。