这个关于神经网络学习规则的深入教程通过示例解释了 Hebbian 学习和感知器学习算法:
感知器和赫布学习:在我们之前的教程中,我们讨论了人工神经网络,它是一种称为神经元的大量互连元素的架构。
这些神经元处理接收到的输入以提供所需的输出。节点或神经元通过输入、连接权重和激活函数连接起来。
神经网络的主要特征是它的学习能力。神经网络用已知的例子训练自己。一旦网络得到训练,它就可以用于解决问题的未知值。
神经网络通过各种学习方案进行学习,这些方案被归类为有监督学习或无监督学习。
在监督学习算法中,目标值是网络已知的。它试图减少所需输出(目标)与实际输出之间的误差,以获得最佳性能。在无监督学习算法中,目标值是未知的,网络通过形成集群等识别输入中的隐藏模式来自行学习。
一个人工神经网络由三部分组成,即输入层、隐藏层和输出层。有一个输入层和输出层,而网络中可能没有隐藏层或 1 个或多个隐藏层。基于这种结构,人工神经网络分为单层、多层、前馈或循环网络。
Hebbian学习介绍,你可以从这个教程学到什么?
- 重要的人工神经网络术语
- 神经网络学习规则比较
- 监督学习算法的分类
- #1) 梯度下降学习
- #2) 随机学习
- 无监督学习算法的分类
- #1) 赫布学习
- #2) 竞争性学习
- 麦卡洛克-皮茨神经元
- Hebbian 学习算法
- Hebbian 学习规则示例
- 感知器学习算法
- 感知器学习规则示例
- Widrow Hoff 学习算法
- 监督学习算法的分类
- 结论
- 推荐阅读
重要的人工神经网络术语
在对 ANN 中的各种学习规则进行分类之前,让我们先了解一些与 ANN 相关的重要术语。
#1) 权重:在 ANN 中,每个神经元通过连接链接与其他神经元相连。这些链接承载着重量。权重包含有关神经元输入信号的信息。权重和输入信号用于获得输出。权重可以用矩阵形式表示,也称为连接矩阵。
每个神经元通过连接权重连接到下一层的每个其他神经元。因此,如果有“n”个节点并且每个节点有“m”个权重,那么权重矩阵将是:
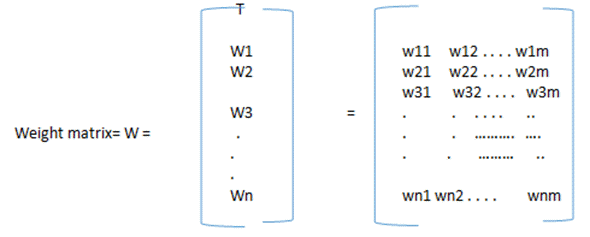
W1表示起始加权向量从节点1 W11表示从1个加权矢量ST前述层到1个的节点ST的下一层的节点。类似地,wij 表示从“第 i 个”处理元素(神经元)到下一层“第 j 个”处理元素的权重向量。
#2) 偏差:通过将输入元素 x (b) = 1 添加到输入向量中,将偏差添加到网络中。偏差还带有由 w (b) 表示的权重。
偏置在计算神经元的输出中起着重要作用。偏差可以是正的,也可以是负的。正偏差会增加净输入权重,而负偏差会减少净输入。
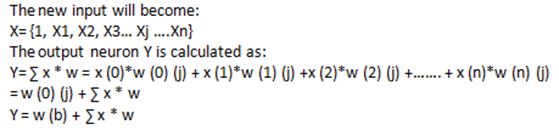
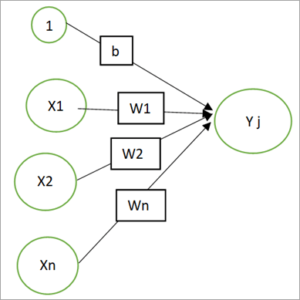
#3) 阈值:在激活函数中使用阈值。将净输入与阈值进行比较以获得输出。在 NN 中,激活函数是根据阈值定义的,并计算输出。
阈值为:
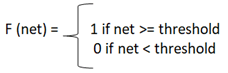
#4) 学习率:用 alpha ? 表示。学习率范围从0到1,用于神经网络学习过程中的权重调整。
#5) 动量因子:添加它是为了更快地收敛结果。动量因子被添加到权重中,通常用于反向传播网络。
神经网络学习规则比较
| 学习方法 -> | 梯度下降 | 赫比 | 竞争的 | 随机 |
|---|---|---|---|---|
| 建筑类型 || | ||||
| 单层前馈 | ADALINE 霍普菲尔德 感知器 | 联想 记忆 霍普菲尔德 | 线性向量 量化 | |
| 多层前馈 | 级联 相关 多层 前馈 径向偏置 函数 | 新认知机 | ||
| 经常性 | 循环神经 网络 | 双向自动 联想 记忆 Brain-State-In-a-Box Hopfield | 自适应 共振理论 | 玻尔兹曼 机 柯西 机 |
ANN的各种学习类型的分类如下所示。
监督学习算法的分类
- 梯度下降
- 随机
#1) 梯度下降学习
在这种类型的学习中,错误减少是在权重和网络激活函数的帮助下发生的。激活函数应该是可微的。
权重的调整取决于本次学习中的误差梯度 E。反向传播规则是此类学习的一个示例。因此权重调整定义为

#2) 随机学习
在这种学习中,权重以概率方式进行调整。
Hebbian学习介绍:无监督学习算法的分类
- 赫比
- 竞争的
#1) 赫布学习
这种学习是由 Hebb 在 1949 年提出的,它基于权重的相关调整。输入和输出模式对与权重矩阵 W 相关联。

输出的转置用于权重调整。
#2) 竞争性学习
这是一个赢家通吃的策略。在这种类型的学习中,当一个输入模式被发送到网络时,该层中的所有神经元都会竞争,只有获胜的神经元才会进行权重调整。
麦卡洛克-皮茨神经元
也称为MP Neuron,这是1943年发现的最早的神经网络。在这个模型中,神经元通过连接权重连接,激活函数以二进制形式使用。阈值用于确定神经元是否会触发。
MP神经元的功能是:
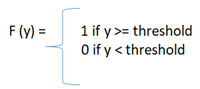
感知器学习算法:Hebbian 学习算法
Hebb Network由 Donald Hebb 于 1949 年提出。根据 Hebb 规则,发现权重与输入和输出的乘积成正比。这意味着在 Hebb 网络中,如果两个神经元相互连接,那么与这些神经元相关的权重可以通过突触间隙的变化来增加。
该网络适用于双极数据。Hebbian 学习规则一般应用于逻辑门。
权重更新为:
W(新)= w(旧)+ x*y
Hebbian 学习规则的训练算法
该算法的训练步骤如下:
- 最初,权重设置为零,即对于所有输入 i = 1 到 n 的 w = 0 并且 n 是输入神经元的总数。
- 让我们成为输出。输入的激活函数通常设置为恒等函数。
- 输出的激活函数也设置为 y=t。
- 权重调整和偏差调整为:
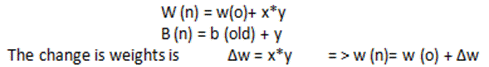
- 对每个输入向量和输出重复步骤 2 到 4。
神经网络学习规则:Hebbian 学习规则示例
感知器和赫布学习:让我们使用 Hebbian Learning 实现带有双极输入的逻辑 AND 函数
X1 和 X2 是输入,b 是偏置为 1,目标值是对输入进行逻辑与运算的输出。
| 输入 | 输入 | 偏见 | 目标 |
|---|---|---|---|
| X1 | X2 | 乙 | 是 |
| 1 | 1 | 1 | 1 |
| 1 | -1 | 1 | -1 |
| -1 | 1 | 1 | -1 |
| -1 | -1 | 1 | -1 |
#1)最初,权重设置为零,偏差也设置为零。
W1=w2=b=0
#2)第一个输入向量取为 [x1 x2 b] = [1 1 1],目标值为 1。
新的权重将是:
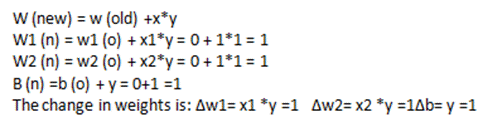
#3)以上权重是最终的新权重。当第二个输入被传递时,这些成为初始权重。
#4)取第二个输入 = [1 -1 1]。目标是-1。
#5)同样,计算其他输入和权重。
下表显示了所有输入:
| 输入 | 偏见 | 目标输出 | 体重变化 | 偏差变化 | 新权重 | ||||
|---|---|---|---|---|---|---|---|---|---|
| X1 | X2 | 乙 | 是 | ?w1 | ?w2 | ?b | W1 | W2 | 乙 |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 1 | -1 | 1 | -1 | -1 | 1 | -1 | 0 | 2 | 0 |
| -1 | 1 | 1 | -1 | 1 | -1 | -1 | 1 | 1 | -1 |
| -1 | -1 | 1 | -1 | 1 | 1 | -1 | 2 | 2 | -2 |
用于 AND 函数的 Hebb Net
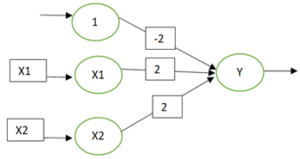
Hebbian学习介绍:感知器学习算法
感知器网络是单层前馈网络。这些也称为单感知器网络。感知器由输入层、隐藏层和输出层组成。
输入层通过权重连接到隐藏层,权重可以是抑制性或兴奋性或零(-1、+1 或 0)。使用的激活函数是输入层和隐藏层的二元阶跃函数。
输出是
Y= f (y)
激活函数为:

权重更新发生在隐藏层和输出层之间以匹配目标输出。根据实际输出和期望输出计算误差。

如果输出与目标匹配,则不会发生权重更新。权重最初设置为 0 或 1,并连续调整,直到找到最佳解决方案。
网络中的权重最初可以设置为任何值。感知器学习将收敛到权重向量,为所有输入训练模式提供正确的输出,并且这种学习发生在有限数量的步骤中。
感知器规则可用于二进制和双极输入。
单输出感知器的学习规则
#1)假设有“n”个训练输入向量,x (n) 和 t (n) 与目标值相关联。
#2)初始化权重和偏差。将它们设置为零以便于计算。
#3)让学习率为 1。
#4)输入层有恒等激活函数,所以 x (i)= s ( i)。
#5)计算网络的输出:

#6)激活函数应用于净输入以获得输出。

#7)现在根据输出,比较所需的目标值 (t) 和实际输出。
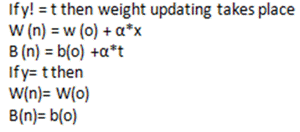
#8)继续迭代直到权重没有变化。一旦达到这个条件就停止。
多输出感知器的学习规则
#1)假设有“n”个训练输入向量,x (n) 和 t (n) 与目标值相关联。
#2)初始化权重和偏差。将它们设置为零以便于计算。
#3)让学习率为 1。
#4)输入层有恒等激活函数,所以 x (i)= s ( i)。
#5)要计算从 j= 1 到 m 的每个输出向量的输出,净输入为:

#6)激活函数应用于净输入以获得输出。

#7)现在根据输出,比较所需的目标值 (t) 和实际输出并进行权重调整。
w 是第 i 个输入和第 j 个输出神经元之间连接链接的权重向量,t 是输出单元 j 的目标输出。
#8)继续迭代直到权重没有变化。一旦达到这个条件就停止。
感知器和赫布学习:感知器学习规则示例
使用感知器网络为双极输入和输出实现 AND 函数。
输入模式将为 x1、x2 和偏差 b。让初始权重为 0,偏差为 0。阈值设置为零,学习率为 1。
与门
| X1 | X2 | 目标 |
|---|---|---|
| 1 | 1 | 1 |
| 1 | -1 | -1 |
| -1 | 1 | -1 |
| -1 | -1 | -1 |
#1) X1=1 , X2= 1 和目标输出 = 1
W1=w2=wb=0 和 x1=x2=b=1, t=1
净输入= y =b + x1*w1+x2*w2 = 0 +1*0 +1*0 =0
由于阈值为零,因此:
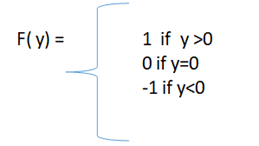
从这里我们得到,输出 = 0。现在检查输出 (y) = 目标 (t)。
y = 0 但 t = 1 这意味着它们不相同,因此权重更新发生。
出现第一个输入向量后,新的权重分别为 1、1 和 1。
#2) X1= 1 X2= -1 , b= 1 and target = -1, W1=1 ,W2=2, Wb=1
净输入= y =b + x1*w1+x2*w2 = 1+1* 1 + (-1)*1 =1
input= 1 的净输出将为 1,来自:
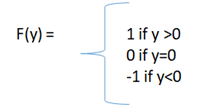
因此,target = -1 与实际输出 =1 不匹配。发生重量更新。
现在新的权重是 w1 = 0 w2 =2 和 wb =0
同样,通过继续下一组输入,我们得到下表:
| 输入 | 偏见 | 目标 | 净投入 | 计算输出 | 体重变化 | 新权重 | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| X1 | X2 | 乙 | 吨 | 阴 | 是 | ?w1 | ?w2 | ?b | W1 | W2 | 白 |
| EPOCH 1 | |||||||||||
| 1 | 1 | 1 | 1 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 |
| 1 | -1 | 1 | -1 | 1 | 1 | -1 | 1 | -1 | 0 | 2 | 0 |
| -1 | 1 | 1 | -1 | 2 | 1 | 1 | -1 | -1 | 1 | 1 | -1 |
| -1 | -1 | 1 | -1 | -3 | -1 | 0 | 0 | 0 | 1 | 1 | -1 |
| EPOCH 2 | |||||||||||
| 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 1 | 1 | -1 |
| 1 | -1 | 1 | -1 | -1 | -1 | 0 | 0 | 0 | 1 | 1 | -1 |
| -1 | 1 | 1 | -1 | -1 | -1 | 0 | 0 | 0 | 1 | 1 | -1 |
| -1 | -1 | 1 | -1 | -3 | -1 | 0 | 0 | 0 | 1 | 1 | -1 |
EPOCHS 是输入到系统的输入模式循环,直到不需要改变权重并且迭代停止。
神经网络学习规则:Widrow Hoff 学习算法
也称为Delta Rule,它遵循线性回归的梯度下降规则。
它使用目标值和输出值之间的差异更新连接权重。它是属于监督学习算法类别的最小均方学习算法。
ADALINE(自适应线性神经网络)和 MADALINE 遵循此规则。与 Perceptron 不同的是,Adaline 网络的迭代不会停止,而是通过减少最小均方误差来收敛。MADALINE 是一个由多个 ADALINE 组成的网络。
delta 学习规则的动机是最小化输出和目标向量之间的误差。
ADALINE 网络中的权重通过以下方式更新:
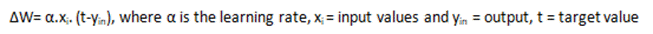
最小均方误差 = (t- y in ) 2,当达到最小均方误差时,ADALINE 收敛。
感知器学习算法结论
在这个感知器和赫布学习教程中,我们讨论了两种算法,即 Hebbian 学习规则和感知器学习规则。Hebbian 规则基于权重向量与输入和学习信号(即输出)成比例增加的规则。通过将输入和输出的乘积与旧权重相加来增加权重。
W(新)= w(旧)+x*y
Hebbian学习介绍:Hebb 规则的应用在于模式关联、分类和归类问题。
感知器学习规则可以应用于单输出和多输出类的网络。感知器网络的目标是将输入模式分类为特定的成员类。输入神经元和输出神经元通过具有权重的链接连接。
调整权重以匹配实际输出与目标值。学习率设置为 0 到 1,它决定了权重的可扩展性。
权重更新如下:

除了这些学习规则之外,机器学习算法还通过许多其他方法进行学习,例如监督、无监督、强化。其他一些常见的 ML 算法是反向传播、ART、Kohonen 自组织映射等。
我们希望你喜欢本机器学习系列的所有教程!!

