曲线拟合教程：Python如何拟合曲线？

2021年9月12日03:06:46 发表评论 6,435 次浏览

曲线拟合是一种优化，它为定义的函数找到一组最适合给定观测值的最佳参数。

Python如何拟合曲线？与监督学习不同，曲线拟合要求您定义将输入示例映射到输出的函数。

Python曲线拟合方式：映射函数，也称为基函数，可以采用您喜欢的任何形式，包括直线（线性回归）、曲线（多项式回归）等等。这提供了定义曲线形式的灵活性和控制，其中使用优化过程来找到函数的特定最优参数。

在本教程中，您将了解如何在 Python 中执行曲线拟合。

完成本教程后，您将了解：

  • 曲线拟合涉及找到将输入示例映射到输出的函数的最佳参数和Python曲线拟合实现。
  • SciPy Python 库提供了一个 API 来将曲线拟合到数据集，Python拟合曲线代码的实现。
  • Python曲线拟合绘图：如何在 SciPy 中使用曲线拟合将一系列不同的曲线拟合到一组观测值。

让我们开始吧。曲线拟合教程：Python如何拟合曲线？

曲线拟合 Python
照片由Gael Varoquaux 提供，保留部分权利。

教程概述

本教程分为三个部分；他们是：

  1. 曲线拟合
  2. 曲线拟合 Python API
  3. 曲线拟合工作示例

曲线拟合

曲线拟合是一个优化问题，它找到一条最适合一组观测值的线。

最容易考虑二维曲线拟合，例如图形。

考虑到我们已经从具有输入和输出的问题域中收集了数据示例。

x 轴是自变量或函数的输入。y 轴是因变量或函数的输出。我们不知道将输入示例映射到输出的函数的形式，但我们怀疑我们可以用标准函数形式近似该函数。

曲线拟合涉及首先定义映射函数（也称为基函数或目标函数）的函数形式，然后搜索导致最小误差的函数参数。

误差是通过使用域中的观察结果并将输入传递给我们的候选映射函数并计算输出来计算的，然后将计算的输出与观察到的输出进行比较。

一旦拟合，我们就可以使用映射函数来内插或外推域中的新点。通常通过映射函数运行输入值序列来计算输出序列，然后创建结果的线图以显示输出如何随输入变化以及线与观察点的拟合程度。

Python曲线拟合实现：曲线拟合的关键是映射函数的形式。

输入和输出之间的直线可以定义如下：

  • y = a * x + b

其中y是计算的输出，x是输入，a和b是使用优化算法找到的映射函数的参数。

这被称为线性方程，因为它是输入的加权和。

在线性回归模型中，这些参数称为系数；在神经网络中，它们被称为权重。

这个方程可以推广到任意数量的输入，这意味着曲线拟合的概念不限于二维（一个输入和一个输出），而是可以有许多输入变量。

例如，两个输入变量的线映射函数可能如下所示：

  • y = a1 * x1 + a2 * x2 + b

该方程不必是一条直线。

我们可以通过添加指数在映射函数中添加曲线。例如，我们可以添加由另一个参数加权的输入的平方版本：

  • y = a * x + b * x^2 + c

这称为多项式回归，平方项表示它是二次多项式。

Python如何拟合曲线？到目前为止，这种类型的线性方程可以通过最小化最小二乘法来拟合，并且可以进行分析计算。这意味着我们可以使用一点线性代数找到参数的最佳值。

我们可能还想在方程中添加其他数学函数，例如正弦、余弦等。每一项都用一个参数加权并加到整体中以给出输出；例如：

  • y = a * sin(b * x) + c

将任意数学函数添加到我们的映射函数通常意味着我们无法解析地计算参数，而是需要使用迭代优化算法。

Python曲线拟合方式：这称为非线性最小二乘法，因为目标函数不再是凸的（它是非线性的）并且不容易求解。

现在我们熟悉了曲线拟合，让我们看看如何在 Python 中执行曲线拟合。

Python曲线拟合实现：曲线拟合 Python API

我们可以在 Python 中为我们的数据集执行曲线拟合。

SciPy 开源库提供了用于通过非线性最小二乘法拟合曲线的curve_fit() 函数。

该函数采用相同的输入和输出数据作为参数，以及要使用的映射函数的名称。

映射函数必须采用输入数据和一些参数的例子。这些剩余的参数将是将通过非线性最小二乘优化过程优化的系数或权重常数。

例如，我们可能将域中的一些观察结果加载为输入变量x和输出变量y。

...
# load input variables from a file
x_values = ...
y_values = ...

接下来，我们需要设计一个映射函数来将一条线拟合到数据中，并将其实现为一个接受输入和参数的 Python 函数。

它可能是一条直线，在这种情况下，它将如下所示：

# objective function
def objective(x, a, b, c):
	return a * x + b

然后我们可以调用curve_fit() 函数使用我们定义的函数将一条直线拟合到数据集。

函数curve_fit()返回映射函数的最佳值，例如系数值。它还返回估计参数的协方差矩阵，但我们现在可以忽略它，如下Python拟合曲线代码。

...
# fit curve
popt, _ = curve_fit(objective, x_values, y_values)

一旦拟合，我们可以使用最优参数和我们的映射函数objective()来计算任意输入的输出。

这可能包括我们已经从域中收集的示例的输出，它可能包括插入观察值的新值，或者它可能包括观察到的限制之外的外推值。

...
# define new input values
x_new = ...
# unpack optima parameters for the objective function
a, b, c = popt
# use optimal parameters to calculate new values
y_new = objective(x_new, a, b, c)

现在我们已经熟悉了曲线拟合 API 的使用，让我们看一个有效的例子。

Python如何拟合曲线？曲线拟合工作示例

我们将开发一条曲线来拟合一些现实世界的经济数据观察结果。

在这个例子中，我们将使用所谓的“ Longley's Economic Regression ”数据集；你可以在这里了解更多信息：

我们将自动下载数据集作为工作示例的一部分。

有七个输入变量和 16 行数据，其中每一行定义了 1947 年至 1962 年之间一年的经济细节摘要。

在这个例子中，我们将探索在人口规模和每年就业人数之间拟合一条线。

下面的示例从 URL 加载数据集，选择输入变量作为“人口”，选择输出变量作为“就业”，并创建一个散点图。

# plot "Population" vs "Employed"
from pandas import read_csv
from matplotlib import pyplot
# load the dataset
url = 'https://raw.githubusercontent.com/jbrownlee/Datasets/master/longley.csv'
dataframe = read_csv(url, header=None)
data = dataframe.values
# choose the input and output variables
x, y = data[:, 4], data[:, -1]
# plot input vs output
pyplot.scatter(x, y)
pyplot.show()

Python曲线拟合绘图：运行示例会加载数据集、选择变量并创建散点图。

我们可以看到两个变量之间存在关系。具体来说，随着人口的增加，雇员总数增加。

认为我们可以为这些数据拟合一条线并不是没有道理的。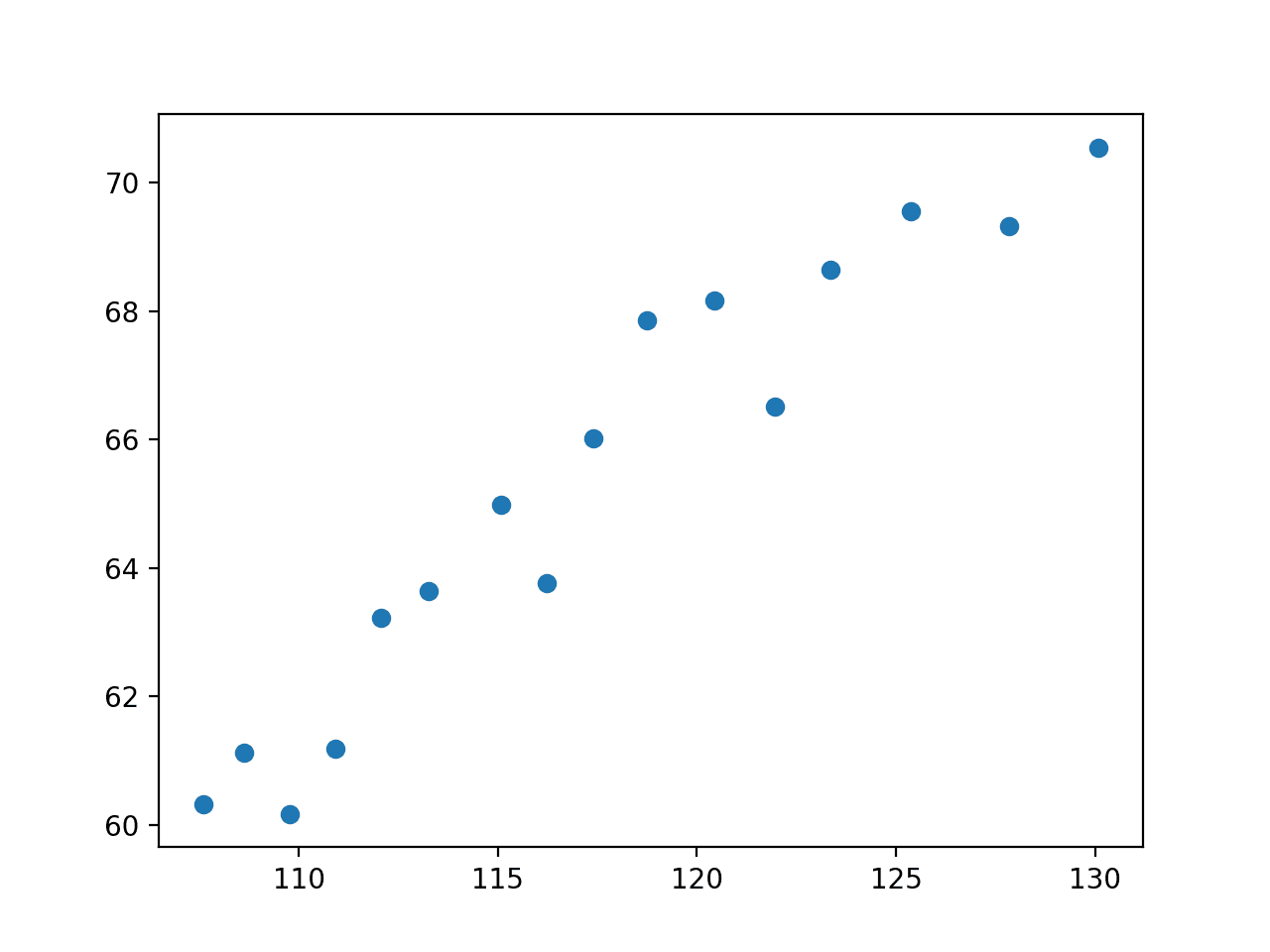曲线拟合教程：Python如何拟合曲线？

人口与总就业人数的散点图

首先，我们将尝试对这些数据拟合一条直线，如下所示：

# define the true objective function
def objective(x, a, b):
	return a * x + b

我们可以使用曲线拟合来找到“ a ”和“ b ”的最佳值并总结找到的值：

...
# curve fit
popt, _ = curve_fit(objective, x, y)
# summarize the parameter values
a, b = popt
print('y = %.5f * x + %.5f' % (a, b))

然后我们可以像以前一样创建散点图。

...
# plot input vs output
pyplot.scatter(x, y)

在散点图的顶部，我们可以为具有优化参数值的函数绘制一条线。

这涉及首先定义在数据集中观察到的最小值和最大值之间的输入值序列（例如，在大约120和大约130之间）。

...
# define a sequence of inputs between the smallest and largest known inputs
x_line = arange(min(x), max(x), 1)

然后我们可以计算每个输入值的输出值。

...
# calculate the output for the range
y_line = objective(x_line, a, b)

然后创建输入与输出的线图以查看一条线：

...
# create a line plot for the mapping function
pyplot.plot(x_line, y_line, '--', color='red')

将这些结合在一起，下面的示例使用曲线拟合为我们的经济数据找到一条直线的参数，下面是完整的Python拟合曲线代码。

# fit a straight line to the economic data
from numpy import arange
from pandas import read_csv
from scipy.optimize import curve_fit
from matplotlib import pyplot

# define the true objective function
def objective(x, a, b):
	return a * x + b

# load the dataset
url = 'https://raw.githubusercontent.com/jbrownlee/Datasets/master/longley.csv'
dataframe = read_csv(url, header=None)
data = dataframe.values
# choose the input and output variables
x, y = data[:, 4], data[:, -1]
# curve fit
popt, _ = curve_fit(objective, x, y)
# summarize the parameter values
a, b = popt
print('y = %.5f * x + %.5f' % (a, b))
# plot input vs output
pyplot.scatter(x, y)
# define a sequence of inputs between the smallest and largest known inputs
x_line = arange(min(x), max(x), 1)
# calculate the output for the range
y_line = objective(x_line, a, b)
# create a line plot for the mapping function
pyplot.plot(x_line, y_line, '--', color='red')
pyplot.show()

运行示例执行曲线拟合并找到我们目标函数的最佳参数。

首先，报告参数的值。

y = 0.48488 * x + 8.38067

接下来，创建一个图，显示原始数据和拟合数据的线。

我们可以看到这是一个相当好的Python曲线拟合绘图。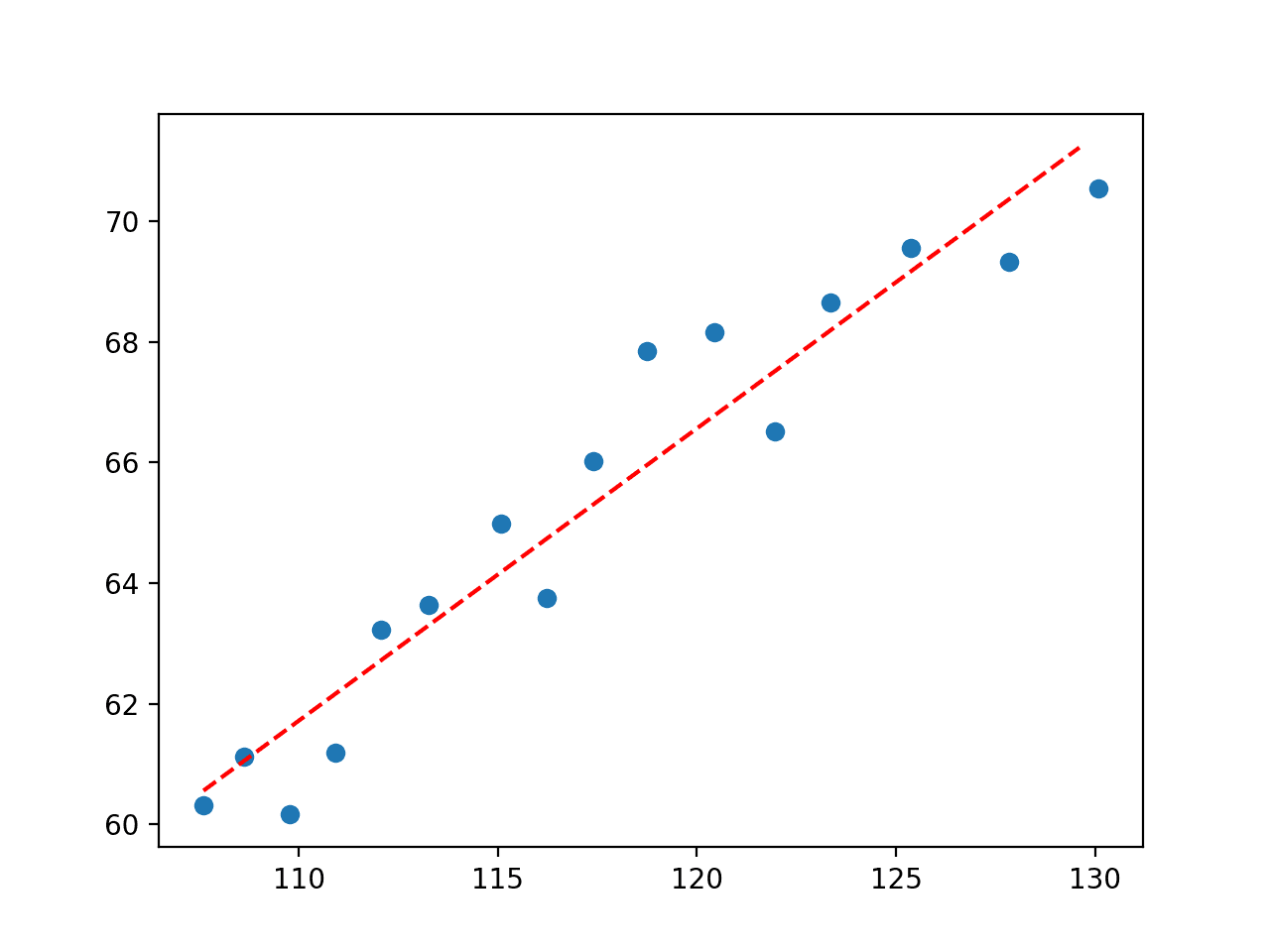曲线拟合教程：Python如何拟合曲线？

拟合经济数据集的直线图

到目前为止，这并不是很令人兴奋，因为我们可以通过在数据集上拟合线性回归模型来实现相同的效果。

Python如何拟合曲线？让我们通过向目标函数添加平方项来尝试多项式回归模型。

# define the true objective function
def objective(x, a, b, c):
	return a * x + b * x**2 + c

将这些结合在一起，下面列出了完整的Python拟合曲线代码示例。

# fit a second degree polynomial to the economic data
from numpy import arange
from pandas import read_csv
from scipy.optimize import curve_fit
from matplotlib import pyplot

# define the true objective function
def objective(x, a, b, c):
	return a * x + b * x**2 + c

# load the dataset
url = 'https://raw.githubusercontent.com/jbrownlee/Datasets/master/longley.csv'
dataframe = read_csv(url, header=None)
data = dataframe.values
# choose the input and output variables
x, y = data[:, 4], data[:, -1]
# curve fit
popt, _ = curve_fit(objective, x, y)
# summarize the parameter values
a, b, c = popt
print('y = %.5f * x + %.5f * x^2 + %.5f' % (a, b, c))
# plot input vs output
pyplot.scatter(x, y)
# define a sequence of inputs between the smallest and largest known inputs
x_line = arange(min(x), max(x), 1)
# calculate the output for the range
y_line = objective(x_line, a, b, c)
# create a line plot for the mapping function
pyplot.plot(x_line, y_line, '--', color='red')
pyplot.show()

首先报告最佳参数。

y = 3.25443 * x + -0.01170 * x^2 + -155.02783

Python曲线拟合绘图：接下来，创建一个图，显示域中观察值上下文中的线。

我们可以看到，与我们首先测试的直线相比，我们定义的二次多项式方程在视觉上更适合数据。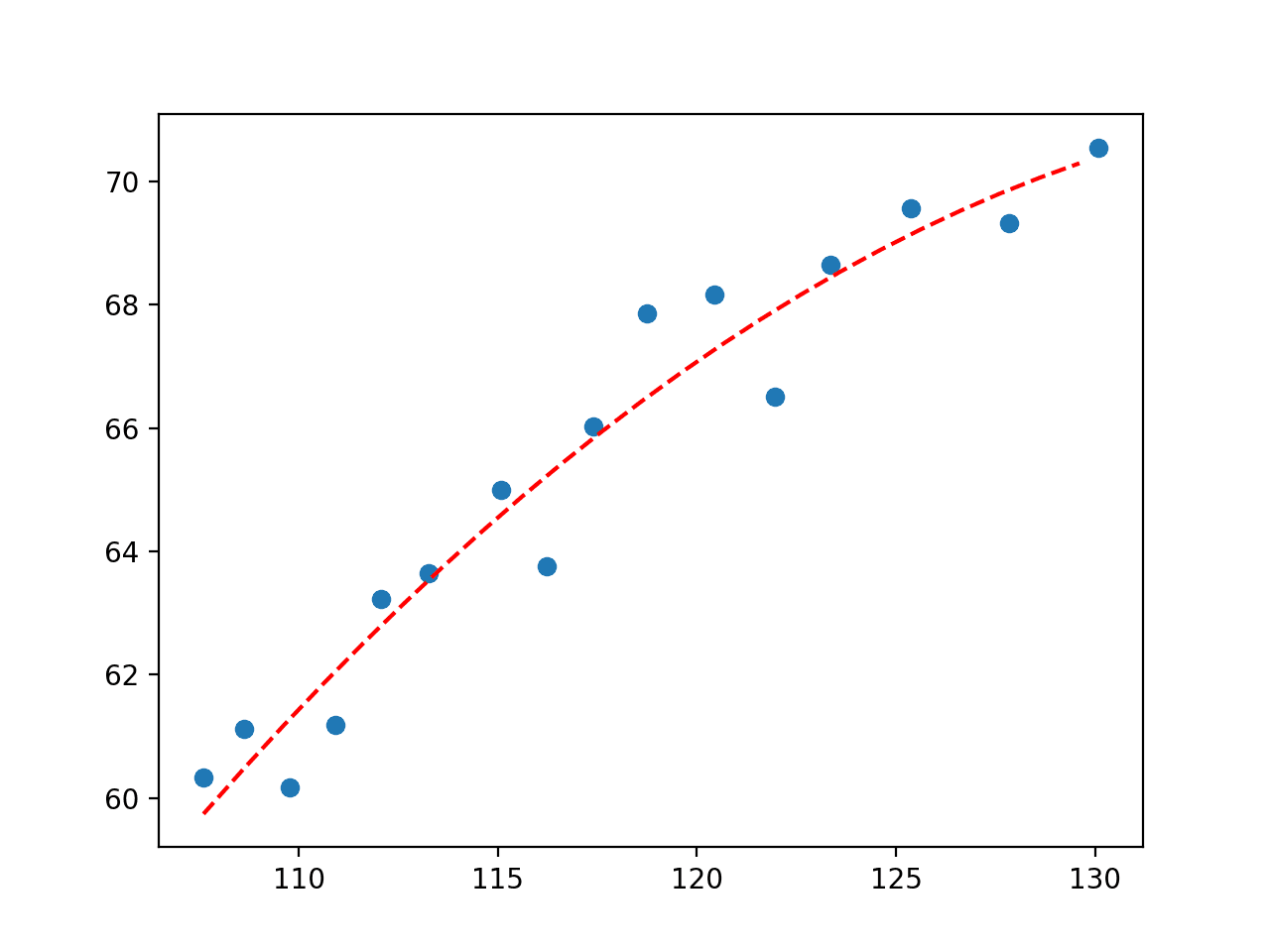曲线拟合教程：Python如何拟合曲线？

拟合经济数据集的二次多项式图

我们可以继续向方程添加更多多项式项，以更好地拟合曲线。

Python曲线拟合实现：例如，下面是对数据进行五次多项式拟合的Python拟合曲线代码示例。

# fit a fifth degree polynomial to the economic data
from numpy import arange
from pandas import read_csv
from scipy.optimize import curve_fit
from matplotlib import pyplot

# define the true objective function
def objective(x, a, b, c, d, e, f):
	return (a * x) + (b * x**2) + (c * x**3) + (d * x**4) + (e * x**5) + f

# load the dataset
url = 'https://raw.githubusercontent.com/jbrownlee/Datasets/master/longley.csv'
dataframe = read_csv(url, header=None)
data = dataframe.values
# choose the input and output variables
x, y = data[:, 4], data[:, -1]
# curve fit
popt, _ = curve_fit(objective, x, y)
# summarize the parameter values
a, b, c, d, e, f = popt
# plot input vs output
pyplot.scatter(x, y)
# define a sequence of inputs between the smallest and largest known inputs
x_line = arange(min(x), max(x), 1)
# calculate the output for the range
y_line = objective(x_line, a, b, c, d, e, f)
# create a line plot for the mapping function
pyplot.plot(x_line, y_line, '--', color='red')
pyplot.show()

Python曲线拟合绘图：运行示例拟合曲线并绘制结果，再次捕捉数据关系如何随时间变化的细微差别。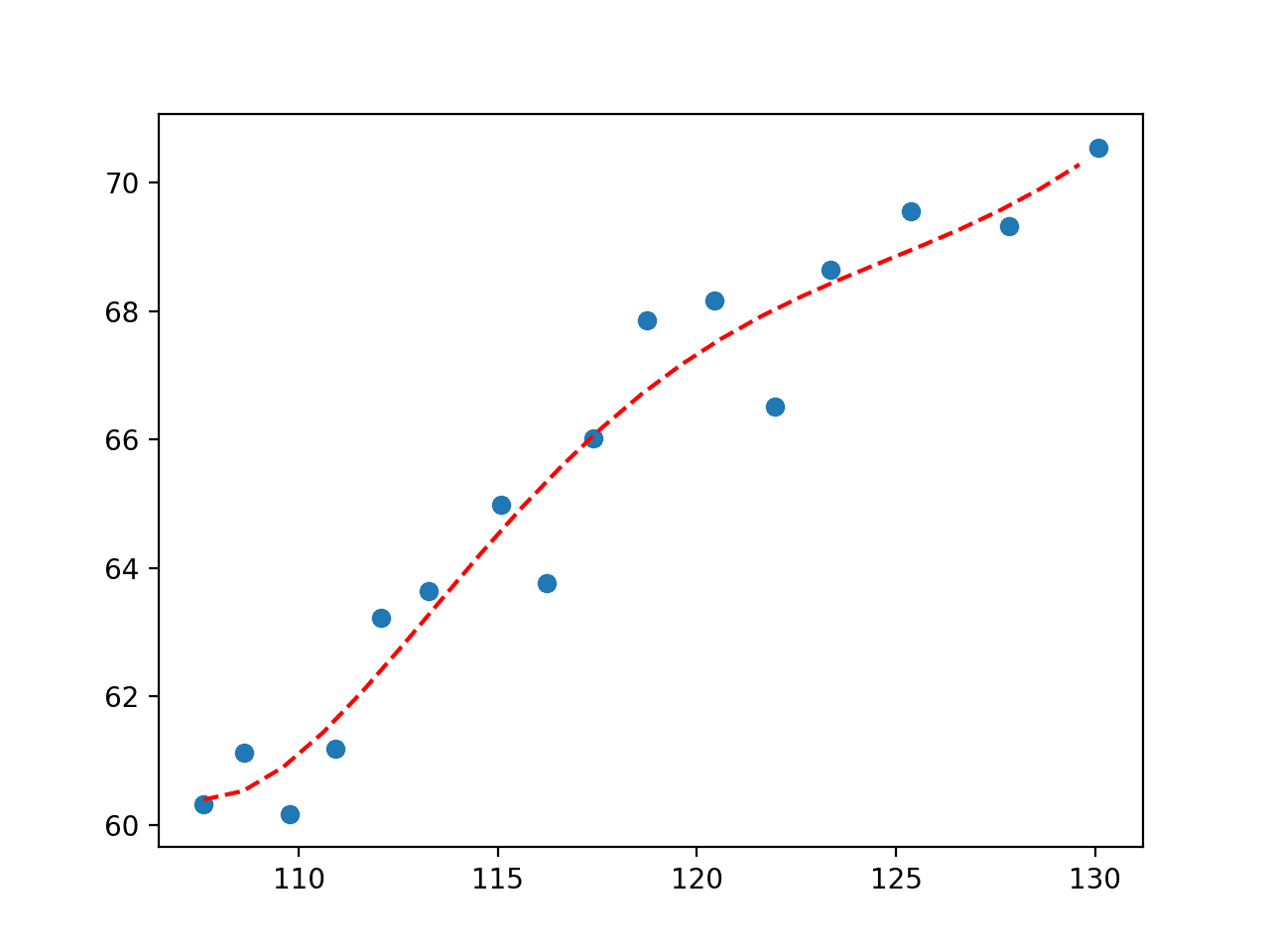曲线拟合教程：Python如何拟合曲线？

Python曲线拟合方式：五阶多项式拟合经济数据集的图

重要的是，我们不限于线性回归或多项式回归。我们可以使用任意的基函数。

例如，也许我们想要一条具有摆动的线来捕捉观察中的短期运动。我们可以在方程中添加一条正弦曲线，并找到最能将该元素整合到方程中的参数。

例如，下面列出了使用正弦波和二次多项式的任意函数：

# define the true objective function
def objective(x, a, b, c, d):
	return a * sin(b - x) + c * x**2 + d

下面列出了使用此基函数拟合曲线的完整示例。

# fit a line to the economic data
from numpy import sin
from numpy import sqrt
from numpy import arange
from pandas import read_csv
from scipy.optimize import curve_fit
from matplotlib import pyplot

# define the true objective function
def objective(x, a, b, c, d):
	return a * sin(b - x) + c * x**2 + d

# load the dataset
url = 'https://raw.githubusercontent.com/jbrownlee/Datasets/master/longley.csv'
dataframe = read_csv(url, header=None)
data = dataframe.values
# choose the input and output variables
x, y = data[:, 4], data[:, -1]
# curve fit
popt, _ = curve_fit(objective, x, y)
# summarize the parameter values
a, b, c, d = popt
print(popt)
# plot input vs output
pyplot.scatter(x, y)
# define a sequence of inputs between the smallest and largest known inputs
x_line = arange(min(x), max(x), 1)
# calculate the output for the range
y_line = objective(x_line, a, b, c, d)
# create a line plot for the mapping function
pyplot.plot(x_line, y_line, '--', color='red')
pyplot.show()

运行Python拟合曲线代码示例拟合曲线并绘制结果。

我们可以看到，添加一个正弦波具有预期的效果，显示具有上升趋势的周期性摆动，这提供了另一种捕获数据关系的方法。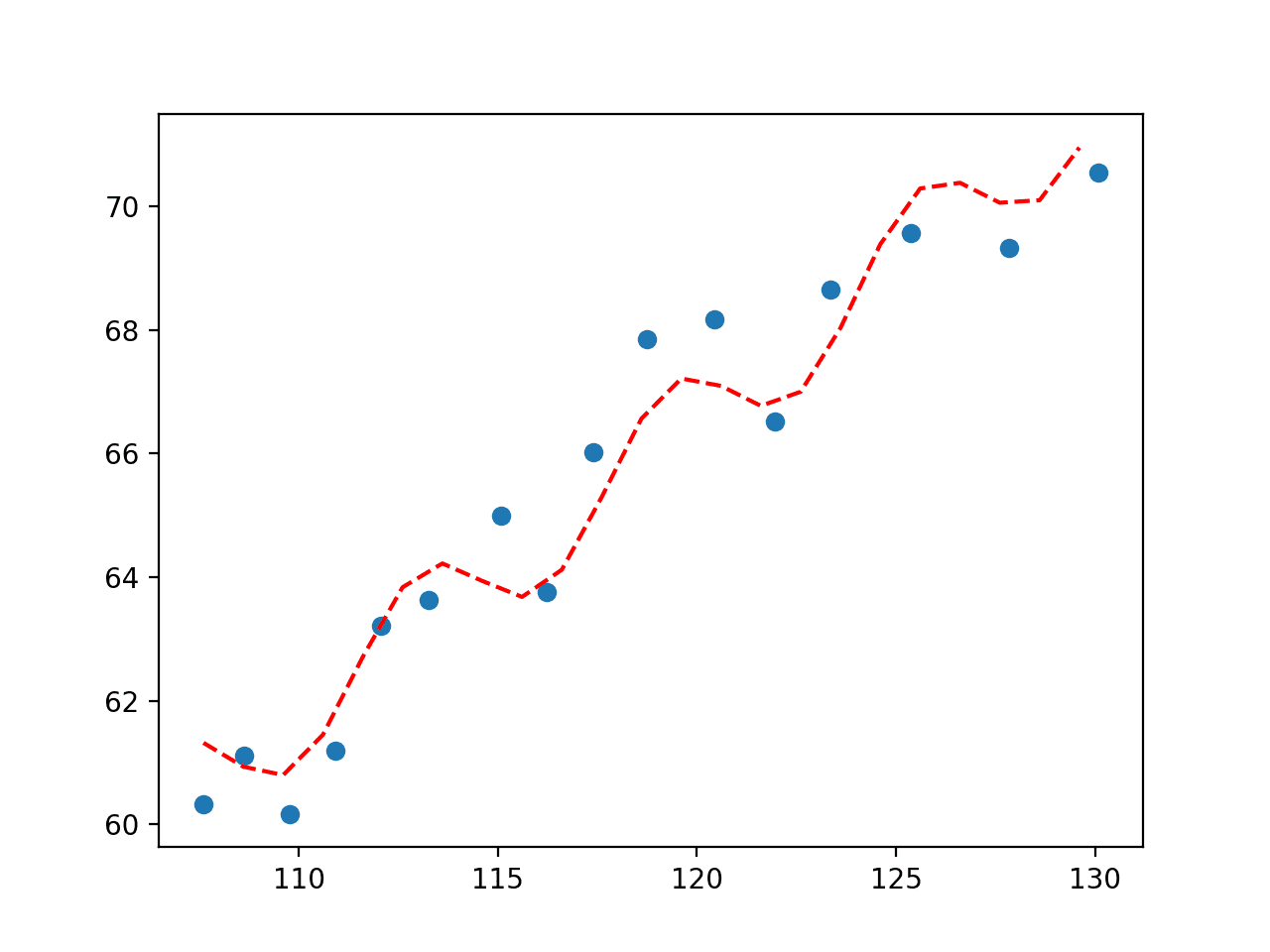曲线拟合教程：Python如何拟合曲线？

Python曲线拟合绘图：拟合经济数据集的正弦波图

你如何选择最合适的？

如果您想要最佳拟合，您可以将问题建模为回归监督学习问题并测试一套算法，以发现哪种算法最能最小化误差。

在这种情况下，当您想要明确定义函数，然后发现最适合数据线的函数参数时，曲线拟合是合适的。

进一步阅读

如果您想深入了解，本节将提供有关该主题的更多资源。

图书

蜜蜂

文章

概括

Python如何拟合曲线？在本教程中，您了解了如何在 Python 中执行曲线拟合以及Python曲线拟合实现。

具体来说，你学到了：

  • 曲线拟合涉及找到将输入示例映射到输出的函数的最佳参数。
  • 与监督学习不同，曲线拟合要求您定义将输入示例映射到输出的函数。
  • 如何在 SciPy 中使用曲线拟合将一系列不同的曲线拟合到一组观测值。

你有任何问题吗？
在下面的评论中提出您的问题，我会尽力回答。

木子山

发表评论

:?: :razz: :sad: :evil: :!: :smile: :oops: :grin: :eek: :shock: :???: :cool: :lol: :mad: :twisted: :roll: :wink: :idea: :arrow: :neutral: :cry: :mrgreen: