GRE数据分析|数据分布，随机变量和概率分布

数据分配：

统计数据集(或总体)的分布是显示数据的所有可能值(或间隔)及其出现频率的列表或函数, 我们可以将分布视为描述观测值之间关系的函数在样本空间中。

例子：

测量了800个电子设备的寿命。由于寿命有许多不同的值, 因此将测量结果分为50个间隔或类, 每个间隔10小时：

601至610小时, 611至620小时, 依此类推, 最多1、091至1、100小时。所得的相对频率分布(作为直方图)具有50条细条和许多不同的条高度, 如下面的数据分析图所示。

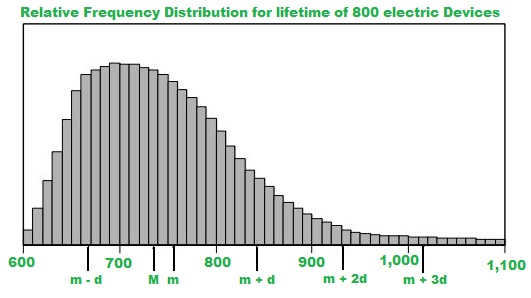
相对频率是某件事发生的频率除以所有结果。作为这里的一个例子，它可以被认为是具有生命周期(Ex 601到610)的电子设备的数量除以总设备。

直方图中，中位数M表示，均值M表示，标准差d表示。

• 中位数由M表示, 介于730和740之间
• 以m表示的平均值介于750和760之间
• 所有50条相对频率的面积之和为1

表示分为许多类的非常大的数据集的直方图具有相对平滑的外观。因此, 可以通过靠近条形图顶部的平滑曲线对分布进行建模。该曲线称为分布曲线。

分布曲线的目的是很好地说明不依赖于特定类别的数值数据的大量分布。分布曲线的属性是, 在任何垂直切片中, 曲线下的面积都像直方图条一样, 代表横轴上相应间隔中的数据比例。

随机变量：

随机变量可以将样本空间中的每个值映射到实数, 而且实数中的值总和始终等于1

例子：

在实验中, 将三枚公平的硬币扔掉, 然后将样本空间

S = { HHH, HHT, HTH, THH, HTT, TTH, THT, TTT}

让变量X计算磁头出现的次数, 因此我们将其称为随机变量。此外, 随机变量通常用X表示。

现在,X可以取值3, 2, 1, 0

P(X = 1) is probability of occurring head one time, P(X = 1) = P(THT) + P(TTH) + P(HTT) = 3/8

随机变量的类型：

离散随机变量：

可以从一组离散值中选取一个值的变量。

例子：

令x表示骰子的总和, 现在x是离散的随机变量, 因为它可以从{{{{2}}, {3} {4}, {5} {7}, {9} {10}, {11}, {12}两个骰子中的一个只能是这些值之一。

连续随机变量：

可以从连续值范围中取一个值的变量。

例子：

x表示500 ml杯子中的水量。现在x可以是0到500之间的数字, x可以取任何一个值。

概率分布：

概率分布指示事件或结果的可能性。

P(x)=随机变量取特定x值的可能性。

例子：

在实验中, 将三枚公平的硬币扔掉, 然后是样本空间,

S = {HHH, HHT, HTH, THH, HTT, TTH, THT, TTT}

X是具有值3、2、1、0的随机变量, 则

P(X = 0) = P(TTT) = 1/8
P(X = 1) = P(HTT) + P(TTH) + P(THT) = 3/8
P(X = 2) = P(HHT) + P(HTH) + P(THH) = 3/8
P(X = 3) = P(HHH) = 1/8

因此,

X(随机变量)	P(X)
0	1/8
1	3/8
2	3/8
3	1/8

该表称为随机变量X的概率分布。

分布可分为2种:

离散分布：

基于离散随机变量, 示例为二项分布, 泊松分布。

连续分配：

基于连续随机变量, 示例为正态分布, 均匀分布, 指数分布。

概率质量函数：

令x为离散随机变量, 则其概率质量函数p(x)定义为

1. p(x) 0
2.  = 1
3. p(x) = P(X=x)

概率密度函数：

令x为连续随机变量, 则定义概率密度函数F(x)使得

1. F(x)  0
2.  = 1
3. P(a <x <b) =

离散分布的属性：

1.  = 1
2. E(x) = 
3. V(x) =

连续分布的属性：

1.  = 1
2. E(x) = 
3. V(x) = 
4. p(a <x <b) =

其中

E(x)表示随机变量x的期望值或平均值,

V(x)表示随机变量x的方差。

分布类型：

• 均匀分布
• 指数分布
• 正态分布
• 二项分布
• 泊松分布

---