处理中的创意编程|S1(Random Walker)
洛伦兹系统是一个常微分方程组, 由美国数学家和气象学家爱德华·诺顿·洛伦兹(Edward Norton Lorenz)于1963年左右首次研究。该系统以对某些参数值和初始条件具有混沌解而著称。它源自地球大气中对流的简化模型。它自然也出现在激光和发电机模型中。洛伦兹吸引子是洛伦兹系统的一组混沌解, 当绘制它们时, 它们类似于蝴蝶或八字形。下图作为Ian Stewart撰写的题为The Lorenz Attractor Exists的文章的一部分, 刊登在2000年8月31日的《自然》杂志上。
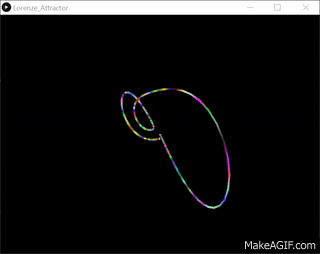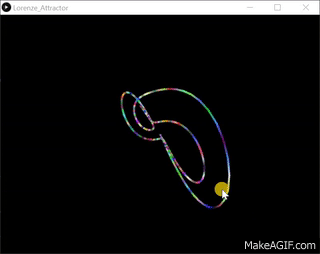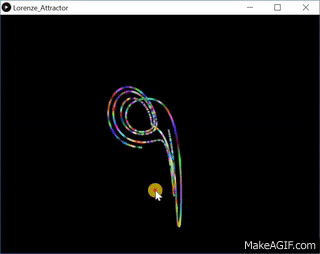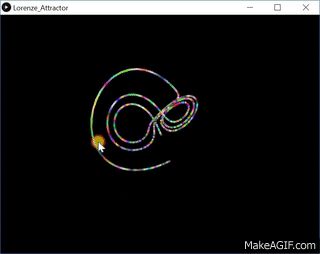
劳伦兹吸引子系统最常表示为3个耦合的非线性微分方程,
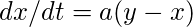
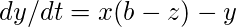
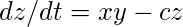
在上述等式中, " a"有时被称为普朗特数, " b"则被称为瑞利数。一组常用的常数是a = 10, b = 28, c = 8 /3。另一组是a = 28, b = 46.92, c = 4。
Java中微分方程的示例实现:
int i = 0 ;
double x0, y0, z0, x1, y1, z1;
double h = 0.01 , a = 10.0 , b = 28.0 , c = 8.0 /3.0 ;
x0 = 0.1 ;
y0 = 0 ;
z0 = 0 ;
for (i = 0 ; i <N; i++) {
x1 = x0 + h * a * (y0 - x0);
y1 = y0 + h * (x0 * (b - z0) - y0);
z1 = z0 + h * (x0 * y0 - c * z0);
x0 = x1;
y0 = y1;
z0 = z1;
//Printing the coordinates
if (i> 100 )
System.out.println(i + " " + x0 + " " + y0 + " " + z0);
}我们将尝试在可视化Java处理中实现上述逻辑。由于我们将在3d中绘制点, 因此我们需要使用3d渲染器。在以下实现中, 我们将使用OPENGL渲染器, 但也可以使用P3D渲染器。我们还需要使用一个名为PeasyCam的外部处理库, 该库可以帮助我们为3d环境工作流创建交互式相机对象。可以使用Processing IDE从工具->添加工具->库下载PeasyCam。
我们还将使用以下函数来表示Lorenz吸引子结构-
- beginShape()–开始记录形状的顶点。
- endShape()–停止记录形状的顶点。
- 顶点()–此功能用于指定点, 线, 三角形, 四边形和多边形的顶点坐标。它仅在beginShape()和endShape()职能。
Lorenz吸引子在Java处理中的实现:-
/* FINAL SKETCH FOR LORENZ ATTRACTOR */
import peasy.*; //Importing peasy package
//Initialization
float x = 0.01 , y = 0 , z = 0 ;
float a = 10 , b = 28 , c = 8.0 /3.0 ;
//ArrayList of PVector objects to store
//the position vectors of the points to be plotted.
ArrayList<PVector> points = new ArrayList<PVector>();
PeasyCam cam; //Declaring PeasyCam object
void setup()
{
//Creating the output window
//and setting up the OPENGL renderer
size( 800 , 600 , OPENGL);
//Initializing the cam object
cam = new PeasyCam( this , 500 );
}
void draw()
{
background( 0 );
//Implementation of the differential equations
float dt = 0.01 ;
float dx = (a * (y - x)) * dt;
float dy = (x * (b - z) - y) * dt;
float dz = (x * y - c * z) * dt;
x += dx;
y += dy;
z += dz;
//Adding the position vectors to points ArrayList
points.add( new PVector(x, y, z));
translate( 0 , 0 , - 80 );
scale( 5 );
stroke( 255 );
noFill();
//Beginning plotting of points
beginShape();
for (PVector v : points) {
//Adding random color to the structure in each frame
stroke(random( 0 , 255 ), random( 0 , 255 ), random( 0 , 255 ));
vertex(v.x, v.y, v.z); //plotting the vertices
}
endShape(); //Drawing ends
}输出:-
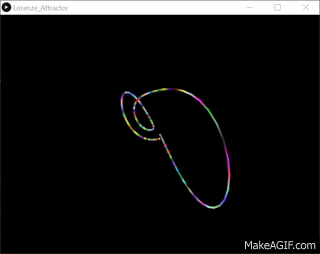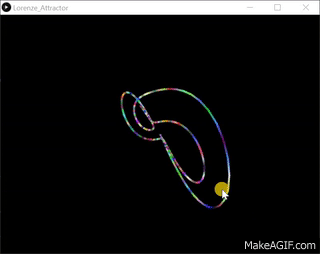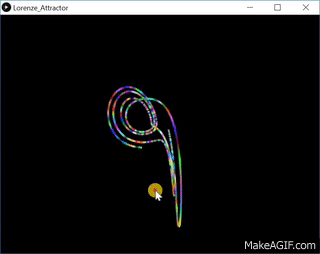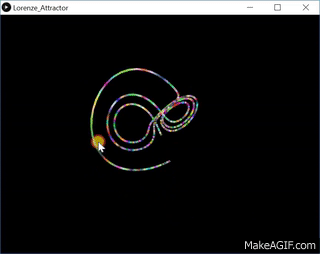
原始资料–
- Daniel Shiffman编写的编码挑战.
- Paul Bourke制作的3D洛伦兹吸引子.
如果发现任何不正确的地方, 或者想分享有关上述主题的更多信息, 请写评论。

![从字法上最小长度N的排列,使得对于正好为K个索引,a[i] a[i]+1](https://www.lsbin.com/wp-content/themes/begin%20lts/img/loading.png)