ML算法：独立成分分析

先决条件：主成分分析

独立成分分析(ICA)是一种机器学习技术, 用于从混合信号中分离出独立的信号源。与主成分分析侧重于最大化数据点的方差不同, 独立成分分析侧重于独立性, 即独立成分。

问题：

从混合信号中提取独立来源的信号, 该混合信号由这些来源的信号组成。

鉴于：

来自五个不同独立来源的混合信号。

目标：

要将混合信号分解为独立的信号源：

• 来源1
• 来源2
• 来源3
• 来源4
• 来源5

解： 独立成分分析(ICA).

考虑

鸡尾酒会问题

or

盲源分离

通过独立成分分析来理解问题。

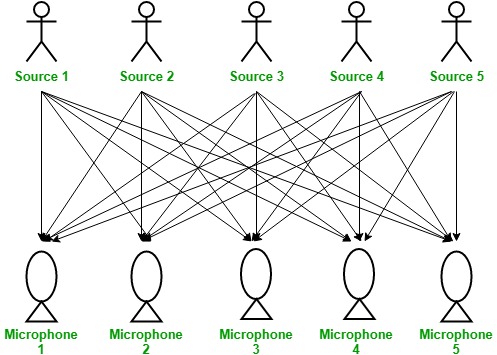
在这里, 有一个聚会正在挤满了人的房间。那个房间里有" n"个发言人, 他们在聚会上同时讲话。在同一房间内, 与正在录制" n"个扬声器的语音信号的扬声器之间的距离不同的地方还有" n"个麦克风。因此, 扬声器的数量等于房间中麦克风的数量。

现在, 通过使用这些麦克风的录音, 我们希望将房间中所有" n"个扬声器的语音信号分离开来, 因为每个麦克风都记录了来自每个扬声器的强度不同的语音信号, 这是由于它们之间的距离不同。通过使用机器学习技术和独立的成分分析, 可以将每个麦克风录音的混合信号分解为独立的来源的语音信号。

[X1, X2, ….., Xn] => [Y1, Y2, ….., Yn]

其中, X1, X2, …, Xn是混合信号中存在的原始信号, 而Y1, Y2, …, Yn是新功能, 并且是彼此独立的独立组件。

ICA限制–

1. 假定ICA生成的独立组件在统计上彼此独立。
2. ICA生成的独立分量必须具有非高斯分布。
3. ICA生成的独立成分的数量等于观察到的混合物的数量。

PCA和ICA之间的区别–

主成分分析	独立成分分析
它减小了尺寸以避免过度装配的问题。	它将混合后的信号分解为独立信号源的信号。
它处理主要成分。	它处理独立组件。
它着重于最大化方差。	它不关注数据点之间的差异问题。
它着重于主成分的相互正交性。	它不关注组件的相互正交性。
它不关注组件的相互独立性。	它着重于组件之间的相互独立性。

---