先决条件:了解逻辑回归和TensorFlow.
Logistic回归摘要:
Logistic回归是机器学习中常用的分类算法。它允许通过从给定的一组标记数据中学习关系来将数据分类为离散类。它从给定的数据集中学习线性关系, 然后以Sigmoid函数的形式引入非线性。
如果是Logistic回归, 则假设为直线的S型, 即
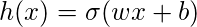
其中
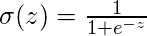
其中,向量w表示Weights,标量b表示模型的Bias。
让我们可视化Sigmoid函数–
import numpy as np
import matplotlib.pyplot as plt
def sigmoid(z):
return 1 /( 1 + np.exp( - z))
plt.plot(np.arange( - 5 , 5 , 0.1 ), sigmoid(np.arange( - 5 , 5 , 0.1 )))
plt.title( 'Visualization of the Sigmoid Function' )
plt.show()输出如下:
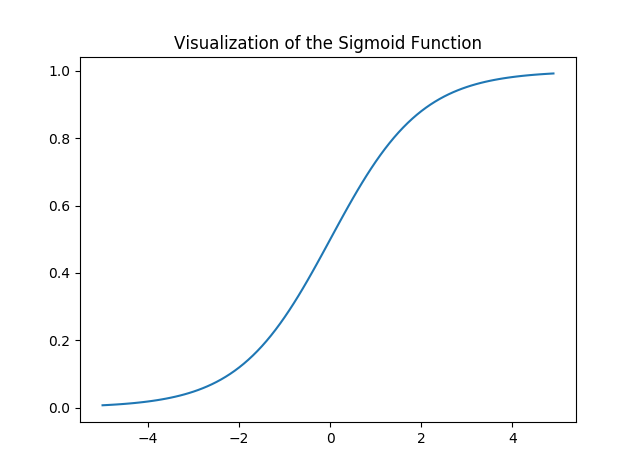
注意,Sigmoid函数的范围是(0,1),这意味着结果值在0和1之间。Sigmoid函数的这一特性使它成为二进制分类的激活函数的一个很好的选择。同样对于z = 0, Sigmoid(z) = 0.5,这是Sigmoid函数范围的中点。
就像线性回归一样,我们需要找到w和b的最优值,使代价函数J最小。在这种情况下,我们将使用Sigmoid交叉熵代价函数由
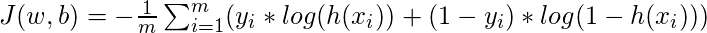
这个成本函数将使用梯度下降进行优化。
实现
我们将从导入必要的库开始。我们将使用Numpy和Tensorflow进行计算,使用Pandas进行基本数据分析,使用Matplotlib进行绘图。我们还将使用Scikit-Learn for One Hot的预处理模块对数据进行编码。
# importing modules
import numpy as np
import pandas as pd
import tensorflow as tf
import matplotlib.pyplot as plt
from sklearn.preprocessing import OneHotEncoder接下来, 我们将导入资料集。我们将使用著名的虹膜数据集.
data = pd.read_csv( 'dataset.csv' , header = None )
print ( "Data Shape:" , data.shape)
print (data.head())输出如下:
Data Shape: (100, 4)
0 1 2 3
0 0 5.1 3.5 1
1 1 4.9 3.0 1
2 2 4.7 3.2 1
3 3 4.6 3.1 1
4 4 5.0 3.6 1现在, 让我们获取特征矩阵和相应的标签并进行可视化。
# Feature Matrix
x_orig = data.iloc[:, 1 : - 1 ].values
# Data labels
y_orig = data.iloc[:, - 1 :].values
print ( "Shape of Feature Matrix:" , x_orig.shape)
print ( "Shape Label Vector:" , y_orig.shape)输出如下:
Shape of Feature Matrix: (100, 2)
Shape Label Vector: (100, 1)可视化给定的数据。
# Positive Data Points
x_pos = np.array([x_orig[i] for i in range ( len (x_orig))
if y_orig[i] = = 1 ])
# Negative Data Points
x_neg = np.array([x_orig[i] for i in range ( len (x_orig))
if y_orig[i] = = 0 ])
# Plotting the Positive Data Points
plt.scatter(x_pos[:, 0 ], x_pos[:, 1 ], color = 'blue' , label = 'Positive' )
# Plotting the Negative Data Points
plt.scatter(x_neg[:, 0 ], x_neg[:, 1 ], color = 'red' , label = 'Negative' )
plt.xlabel( 'Feature 1' )
plt.ylabel( 'Feature 2' )
plt.title( 'Plot of given data' )
plt.legend()
plt.show()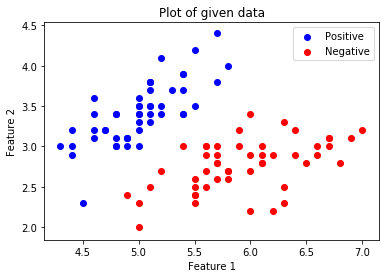
.
现在, 我们将对数据进行热编码以使其与算法一起工作。一种热编码将分类特征转换为一种与分类和回归算法更好地结合的格式。我们还将设置学习率和时期数。
# Creating the One Hot Encoder
oneHot = OneHotEncoder()
# Encoding x_orig
oneHot.fit(x_orig)
x = oneHot.transform(x_orig).toarray()
# Encoding y_orig
oneHot.fit(y_orig)
y = oneHot.transform(y_orig).toarray()
alpha, epochs = 0.0035 , 500
m, n = x.shape
print ( 'm =' , m)
print ( 'n =' , n)
print ( 'Learning Rate =' , alpha)
print ( 'Number of Epochs =' , epochs)输出如下:
m = 100
n = 7
Learning Rate = 0.0035
Number of Epochs = 500现在, 我们将通过定义占位符开始创建模型X和ÿ, 以便我们提供培训示例X和ÿ在培训过程中进入优化器。我们还将创建可训练的变量w ^和b可以通过"梯度下降优化器"进行优化。
# There are n columns in the feature matrix
# after One Hot Encoding.
X = tf.placeholder(tf.float32, [ None , n])
# Since this is a binary classification problem, # Y can take only 2 values.
Y = tf.placeholder(tf.float32, [ None , 2 ])
# Trainable Variable Weights
W = tf.Variable(tf.zeros([n, 2 ]))
# Trainable Variable Bias
b = tf.Variable(tf.zeros([ 2 ]))现在声明"假设", "成本"函数, "优化器"和"全局变量初始化器"。
# Hypothesis
Y_hat = tf.nn.sigmoid(tf.add(tf.matmul(X, W), b))
# Sigmoid Cross Entropy Cost Function
cost = tf.nn.sigmoid_cross_entropy_with_logits(
logits = Y_hat, labels = Y)
# Gradient Descent Optimizer
optimizer = tf.train.GradientDescentOptimizer(
learning_rate = alpha).minimize(cost)
# Global Variables Initializer
init = tf.global_variables_initializer()在Tensorflow会话中开始训练过程。
# Starting the Tensorflow Session
with tf.Session() as sess:
# Initializing the Variables
sess.run(init)
# Lists for storing the changing Cost and Accuracy in every Epoch
cost_history, accuracy_history = [], []
# Iterating through all the epochs
for epoch in range (epochs):
cost_per_epoch = 0
# Running the Optimizer
sess.run(optimizer, feed_dict = {X : x, Y : y})
# Calculating cost on current Epoch
c = sess.run(cost, feed_dict = {X : x, Y : y})
# Calculating accuracy on current Epoch
correct_prediction = tf.equal(tf.argmax(Y_hat, 1 ), tf.argmax(Y, 1 ))
accuracy = tf.reduce_mean(tf.cast(correct_prediction, tf.float32))
# Storing Cost and Accuracy to the history
cost_history.append( sum ( sum (c)))
accuracy_history.append(accuracy. eval ({X : x, Y : y}) * 100 )
# Displaying result on current Epoch
if epoch % 100 = = 0 and epoch ! = 0 :
print ( "Epoch " + str (epoch) + " Cost: "
+ str (cost_history[ - 1 ]))
Weight = sess.run(W) # Optimized Weight
Bias = sess.run(b) # Optimized Bias
# Final Accuracy
correct_prediction = tf.equal(tf.argmax(Y_hat, 1 ), tf.argmax(Y, 1 ))
accuracy = tf.reduce_mean(tf.cast(correct_prediction, tf.float32))
print ( "\nAccuracy:" , accuracy_history[ - 1 ], "%" )输出如下:
Epoch 100 Cost: 125.700202942
Epoch 200 Cost: 120.647117615
Epoch 300 Cost: 118.151592255
Epoch 400 Cost: 116.549999237
Accuracy: 91.0000026226 %让我们绘制各个时期的成本变化。
plt.plot( list ( range (epochs)), cost_history)
plt.xlabel( 'Epochs' )
plt.ylabel( 'Cost' )
plt.title( 'Decrease in Cost with Epochs' )
plt.show()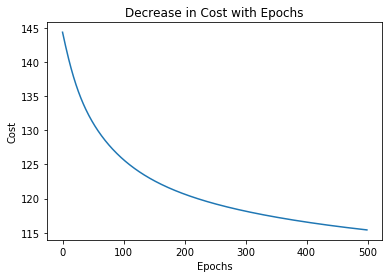
绘制历时精度的变化。
plt.plot( list ( range (epochs)), accuracy_history)
plt.xlabel( 'Epochs' )
plt.ylabel( 'Accuracy' )
plt.title( 'Increase in Accuracy with Epochs' )
plt.show()
现在, 我们将为我们训练有素的分类器绘制"决策边界"。决策边界是一个超曲面, 将基础向量空间划分为两组, 每个类别一组。
# Calculating the Decision Boundary
decision_boundary_x = np.array([np. min (x_orig[:, 0 ]), np. max (x_orig[:, 0 ])])
decision_boundary_y = ( - 1.0 /Weight[ 0 ]) *
(decision_boundary_x * Weight + Bias)
decision_boundary_y = [ sum (decision_boundary_y[:, 0 ]), sum (decision_boundary_y[:, 1 ])]
# Positive Data Points
x_pos = np.array([x_orig[i] for i in range ( len (x_orig))
if y_orig[i] = = 1 ])
# Negative Data Points
x_neg = np.array([x_orig[i] for i in range ( len (x_orig))
if y_orig[i] = = 0 ])
# Plotting the Positive Data Points
plt.scatter(x_pos[:, 0 ], x_pos[:, 1 ], color = 'blue' , label = 'Positive' )
# Plotting the Negative Data Points
plt.scatter(x_neg[:, 0 ], x_neg[:, 1 ], color = 'red' , label = 'Negative' )
# Plotting the Decision Boundary
plt.plot(decision_boundary_x, decision_boundary_y)
plt.xlabel( 'Feature 1' )
plt.ylabel( 'Feature 2' )
plt.title( 'Plot of Decision Boundary' )
plt.legend()
plt.show()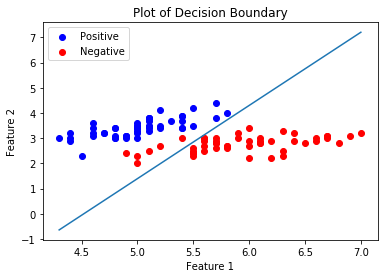
首先, 你的面试准备可通过以下方式增强你的数据结构概念:Python DS课程。

