ML算法：均值漂移聚类详细介绍

2021年5月6日16:42:07 发表评论 1,021 次浏览

均值漂移与无监督学习相反, 无监督学习通过将点朝着模式转移来将数据点迭代地分配给聚类(在均值偏移的情况下, 模式是该区域中数据点的最高密度)。因此, 它也被称为寻模算法。均值漂移算法在图像处理和计算机视觉领域具有应用。

给定一组数据点, 该算法会迭代地将每个数据点分配给最接近的聚类质心, 而最接近的聚类质心的方向则取决于附近大多数点的位置。因此, 每次迭代时, 每个数据点都将移近最靠近点的位置, 即指向或将指向群集中心的位置。当算法停止时, 将每个点分配给一个群集。

与流行的K均值聚类算法不同, 均值平移不需要预先指定聚类数。簇的数量由算法针对数据确定。

注意：均值平移的不利之处在于它在计算上很昂贵O(n²)。

内核密度估计–

应用均值漂移聚类算法的第一步是以数学方式表示数据, 这意味着将数据表示为点(例如下面的集合)。

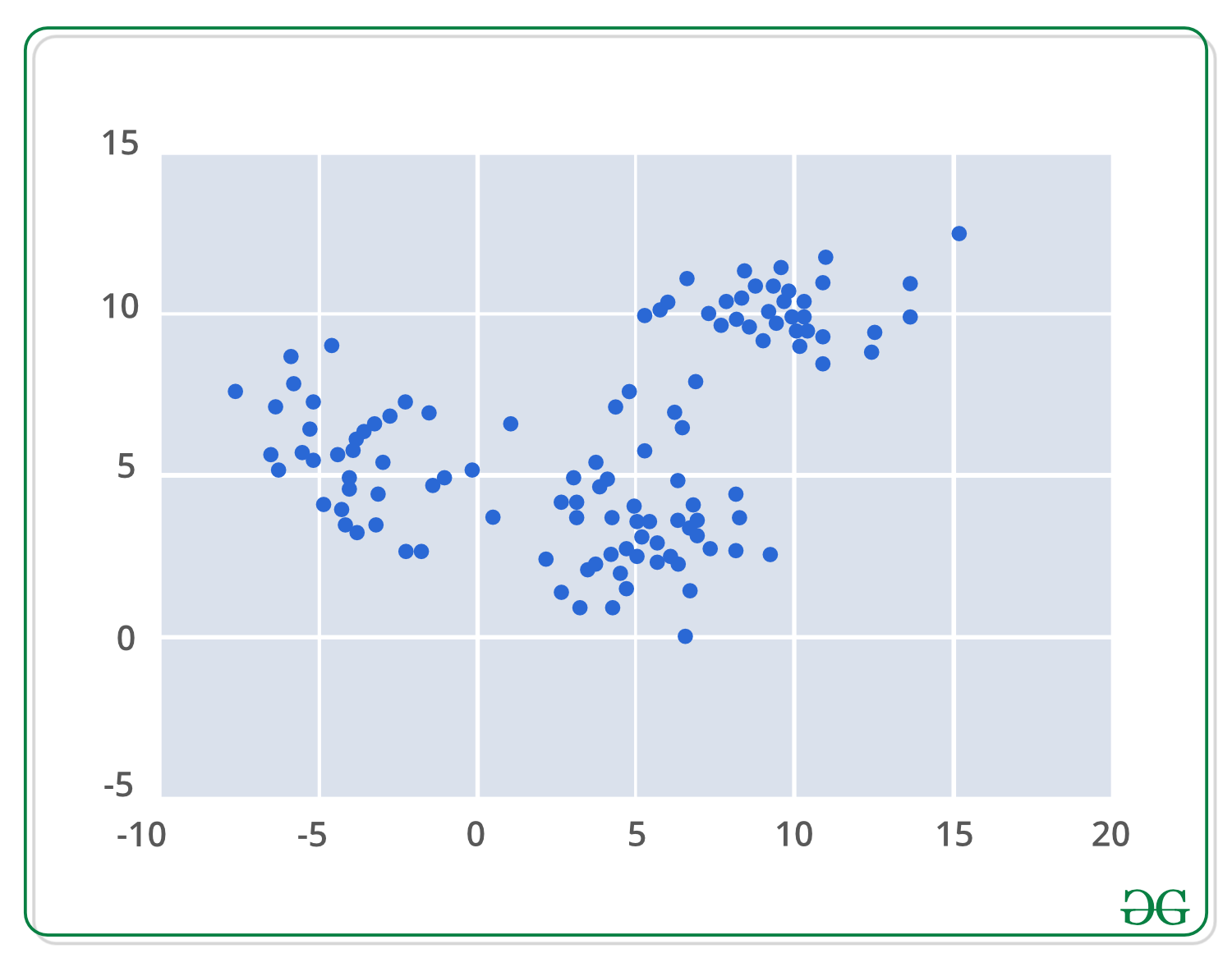
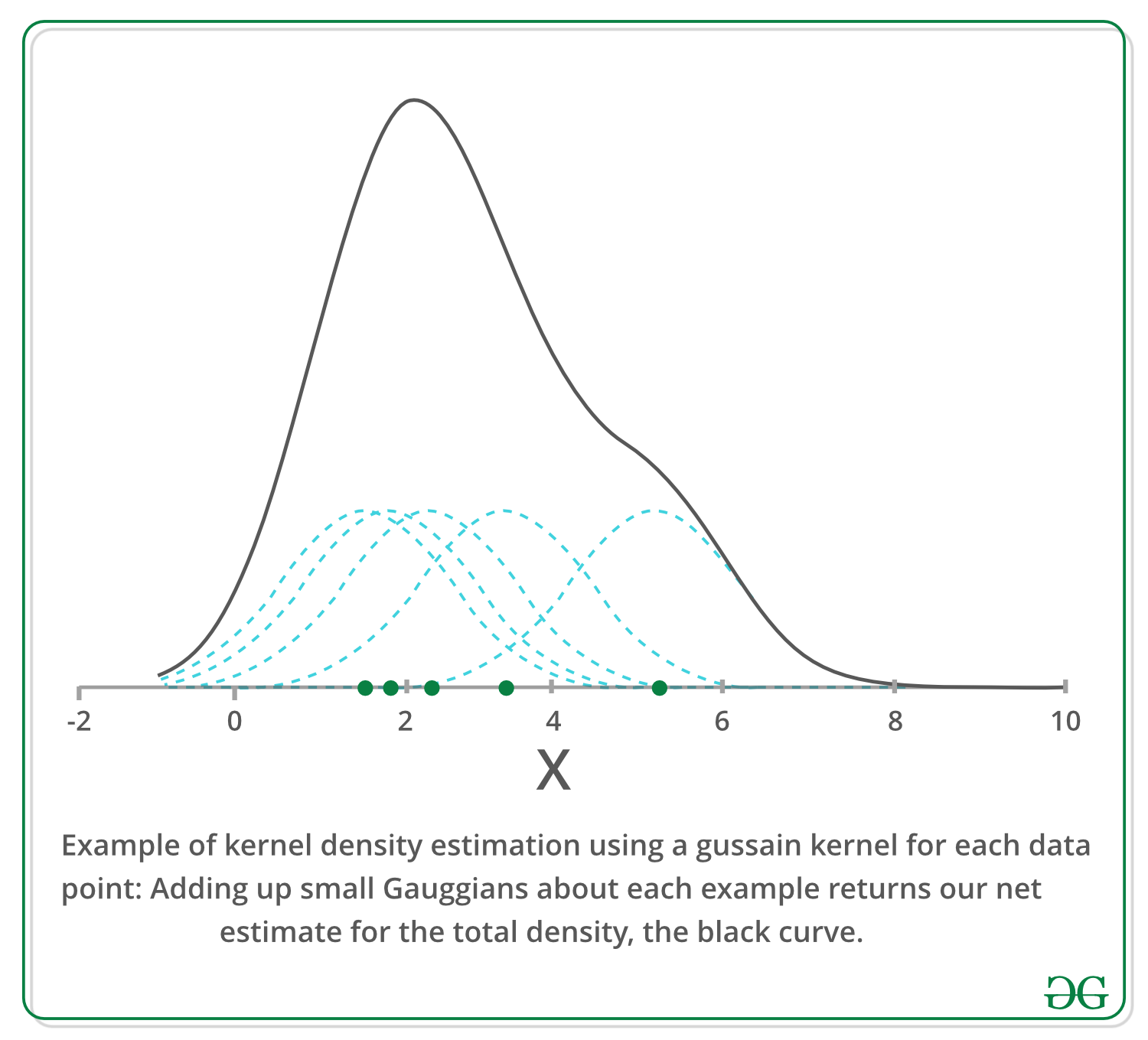
基于核密度估计概念的均值漂移是排序KDE。想象一下, 以上数据是从概率分布中采样的。 KDE是一种估计基础分布的方法, 也称为一组数据的概率密度函数。

它通过在数据集中的每个点上放置一个内核来工作。内核是卷积中通常使用的加权函数的数学术语。内核的类型很多, 但是最受欢迎的是高斯内核。将所有单个内核相加会生成概率表面示例密度函数。根据所使用的内核带宽参数, 所得的密度函数将有所不同。

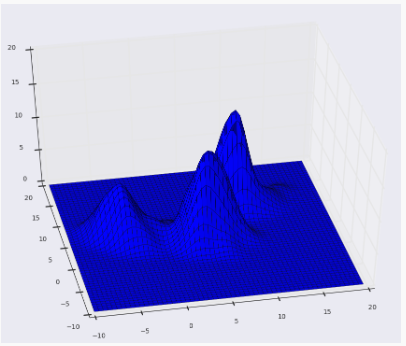
以下是我们使用高斯内核且内核带宽为2的上述点的KDE曲面。

表面图：

等高线图：

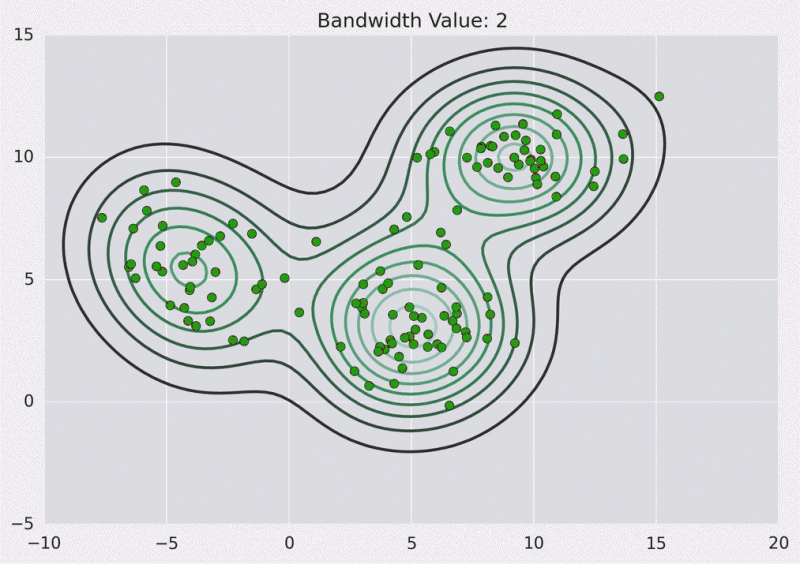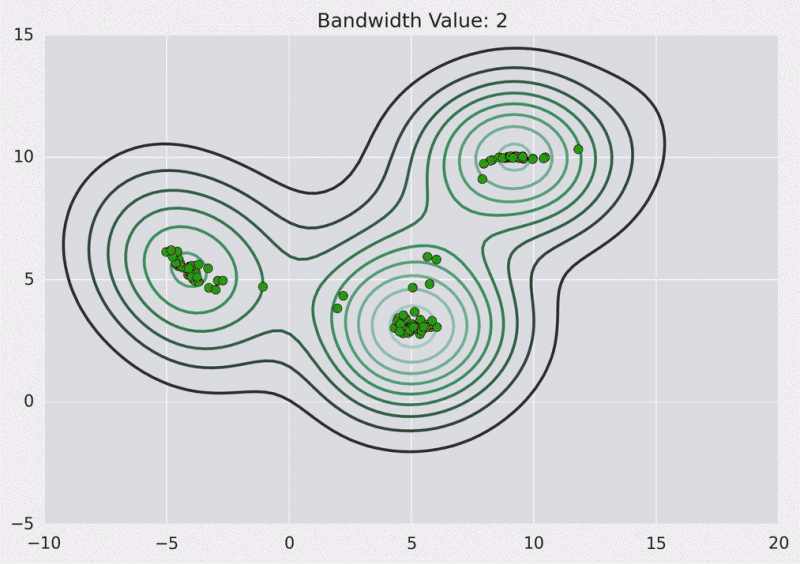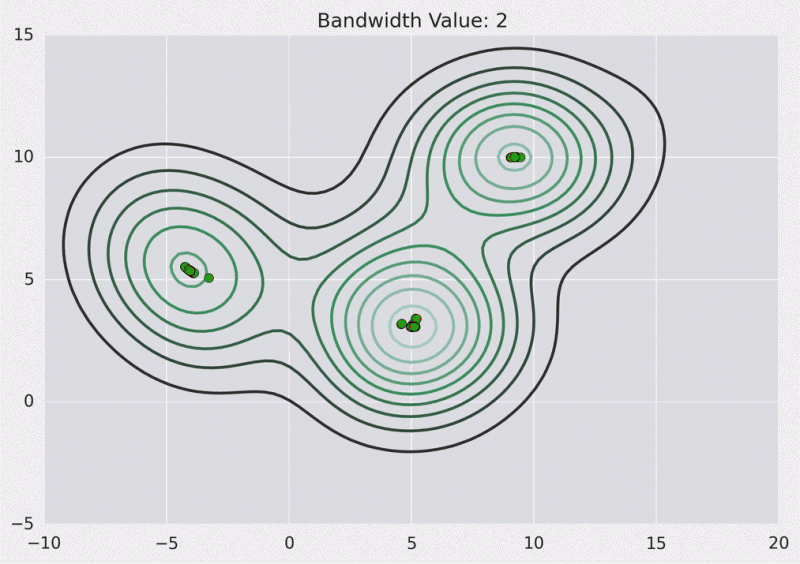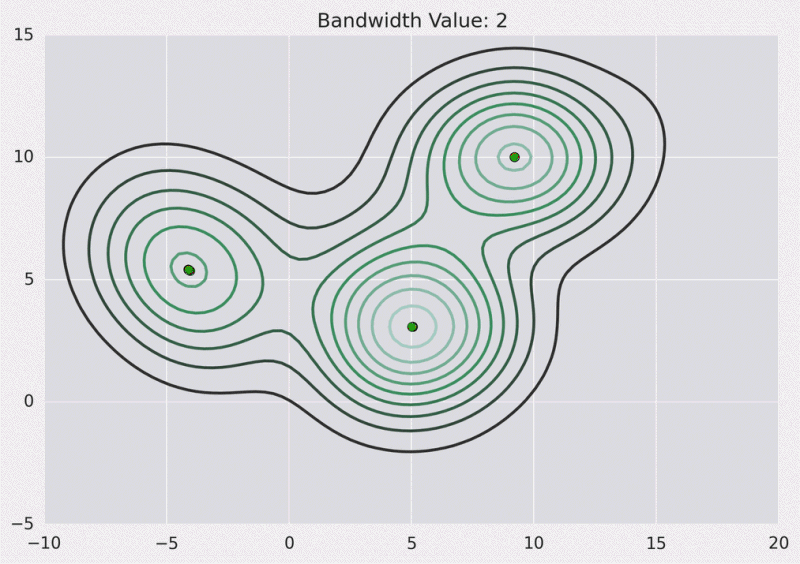
以下是Python实现：

import numpy as np
import pandas as pd
from sklearn.cluster import MeanShift
from sklearn.datasets.samples_generator import make_blobs
from matplotlib import pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
   
# We will be using the make_blobs method
# in order to generate our own data.
  
clusters = [[ 2 , 2 , 2 ], [ 7 , 7 , 7 ], [ 5 , 13 , 13 ]]
  
X, _ = make_blobs(n_samples = 150 , centers = clusters, cluster_std = 0.60 )
   
# After training the model, We store the
# coordinates for the cluster centers
ms = MeanShift()
ms.fit(X)
cluster_centers = ms.cluster_centers_
   
# Finally We plot the data points
# and centroids in a 3D graph.
fig = plt.figure()
  
ax = fig.add_subplot( 111 , projection = '3d' )
  
ax.scatter(X[:, 0 ], X[:, 1 ], X[:, 2 ], marker = 'o' )
  
ax.scatter(cluster_centers[:, 0 ], cluster_centers[:, 1 ], cluster_centers[:, 2 ], marker = 'x' , color = 'red' , s = 300 , linewidth = 5 , zorder = 10 )
  
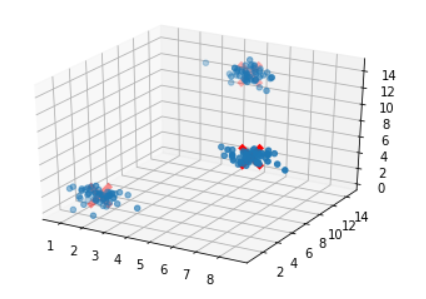
plt.show()

在这里尝试代码

输出如下：

为了说明, 假设我们获得了一个d维空间中的点数据集{ui}, 该数据集是从一些较大的总体中采样的, 并且我们选择了一个具有带宽参数h的内核K。这些数据和内核函数一起返回以下总体密度函数的内核密度估计器。

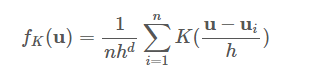
需要此处的内核功能才能满足以下两个条件：

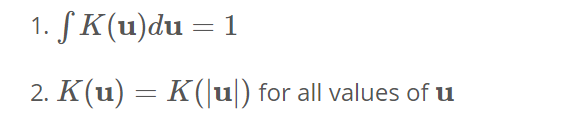
->首先需要确保我们的估算被标准化。 ->第二个与我们空间的对称性有关。

满足这些条件的两个流行的内核函数由-

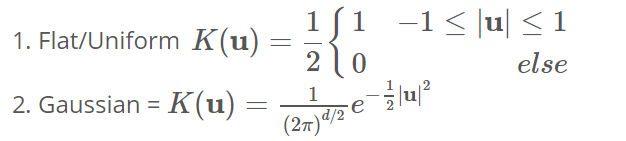
下面, 我们使用高斯核在一个维度上绘制一个示例, 以估计x轴上某些种群的密度。我们可以看到, 每个采样点都在估计值的周围增加了一个小的高斯分布, 上面的方程序可能看起来有些吓人, 但此处的图形应阐明该概念非常简单。

迭代模式搜索–

1. Initialize random seed and window W.
2. Calculate the center of gravity (mean) of W.    
3. Shift the search window to the mean.    
4. Repeat Step 2 until convergence.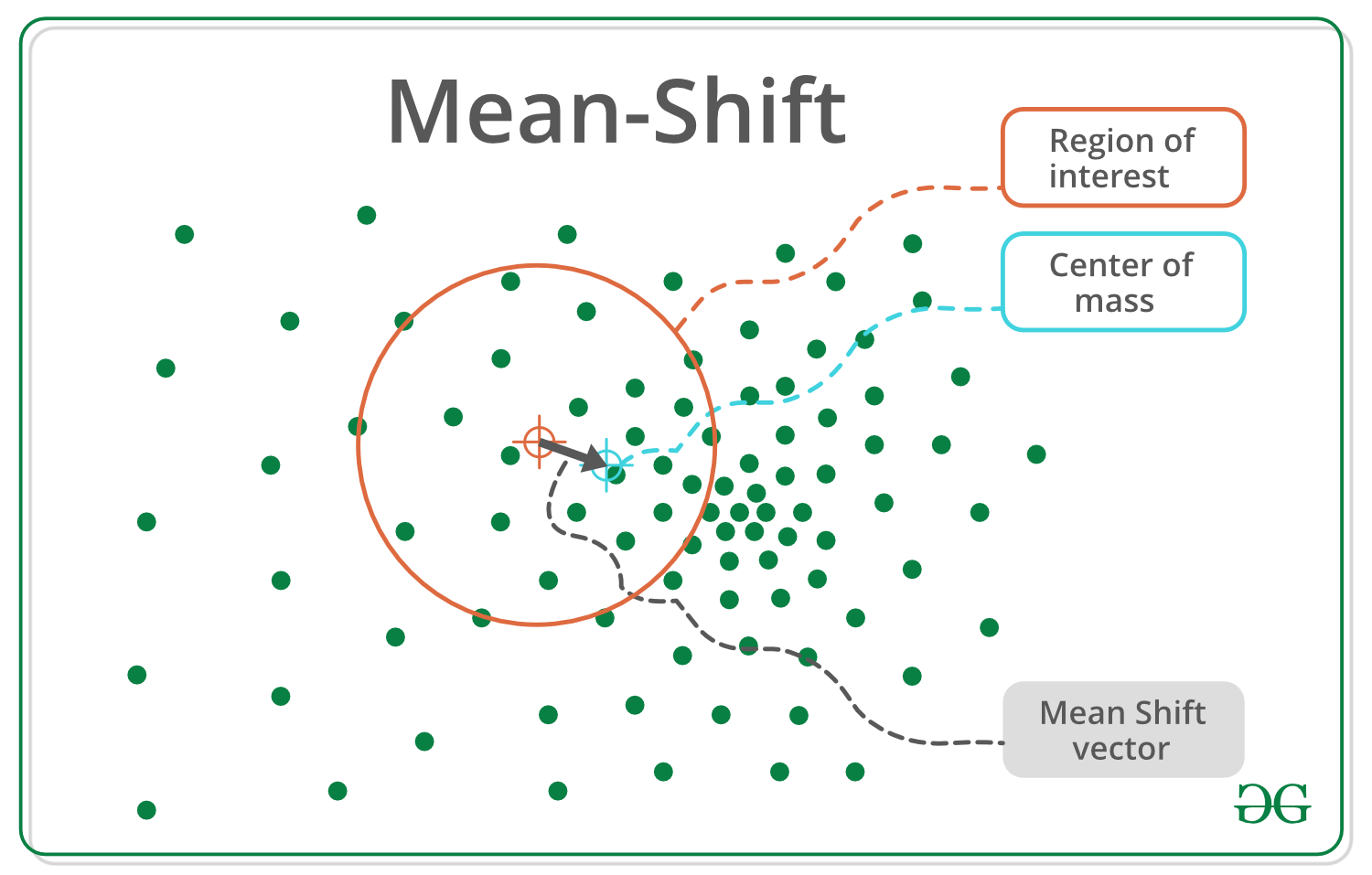

一般算法概述–

for p in copied_points:
     while not at_kde_peak:
         p = shift(p, original_points)

Shift功能看起来像这样–

def shift(p, original_points):
     shift_x = float ( 0 )
     shift_y = float ( 0 )
     scale_factor = float ( 0 )
  
     for p_temp in original_points:
         # numerator
         dist = euclidean_dist(p, p_temp)
         weight = kernel(dist, kernel_bandwidth)
         shift_x + = p_temp[ 0 ] * weight
         shift_y + = p_temp[ 1 ] * weight
         # denominator
         scale_factor + = weight
  
     shift_x = shift_x /scale_factor
     shift_y = shift_y /scale_factor
     return [shift_x, shift_y]

优点：