ML算法：迷你批量K均值聚类算法

2021年5月5日13:41:10 发表评论 1,108 次浏览

先决条件：K均值聚类中K的最优值

K均值是最流行的聚类算法之一, 主要是因为其良好的时间性能。随着所分析的数据集大小的增加, K均值的计算时间增加了, 因为它需要在主存储器中存储整个数据集。由于这个原因, 已经提出了几种方法来减少算法的时间和空间成本。另一种方法是迷你批量K均值算法.

迷你批量K均值算法

主要思想是使用固定大小的随机小批量数据, 以便将其存储在内存中。每次迭代都会从数据集中获得一个新的随机样本, 并将其用于更新聚类, 并将其重复进行直到收敛为止。每个小型批处理使用原型值和数据的凸组合更新聚类, 并采用随着迭代次数降低的学习率。该学习率是在此过程中分配给集群的数据数量的倒数。随着迭代次数的增加, 新数据的影响会降低, 因此当在几个连续的迭代中群集中没有发生变化时, 可以检测到收敛。

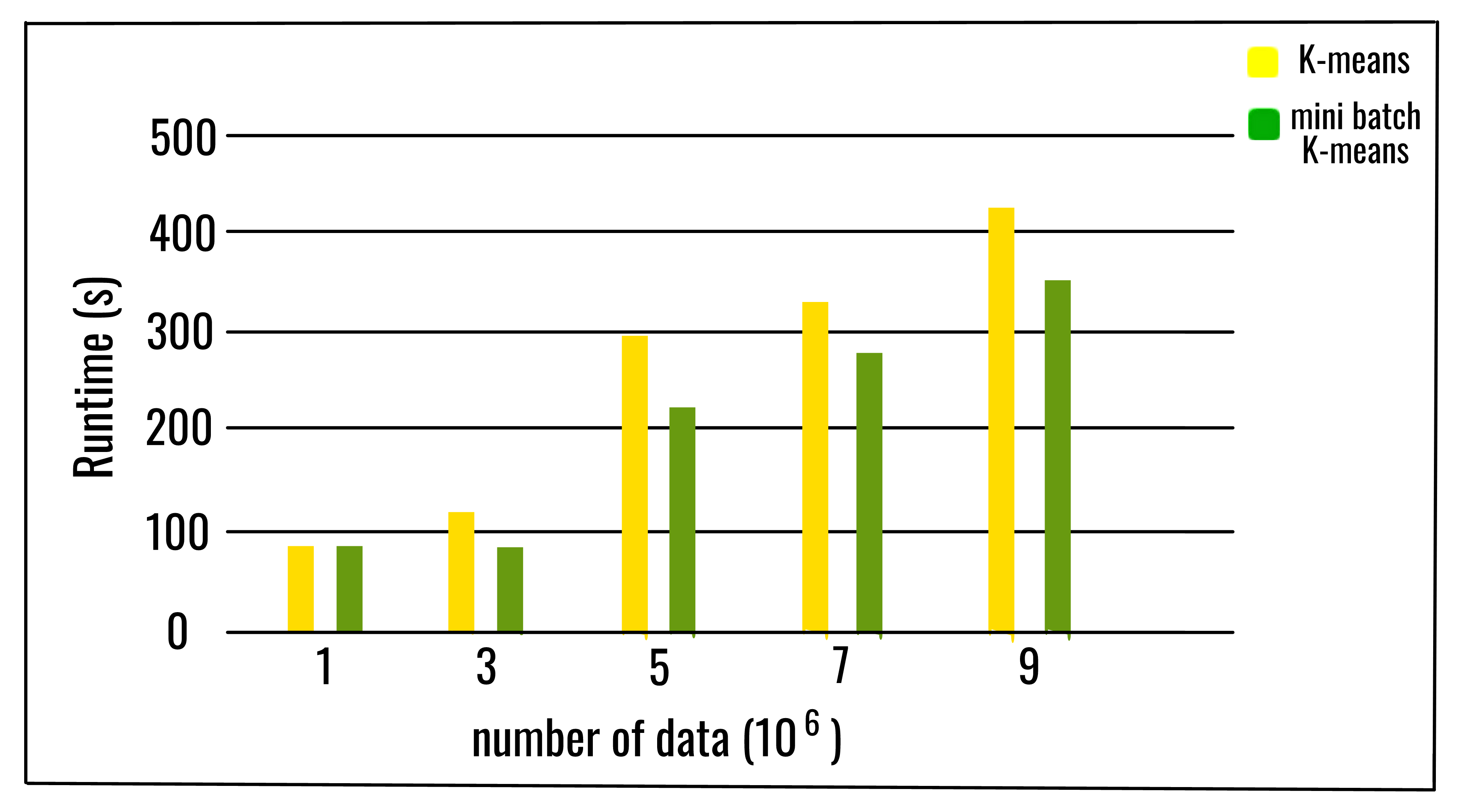
实验结果表明, 它可以节省大量的计算时间, 但会损失一些聚类质量, 但是尚未对该算法进行广泛的研究以测量数据集的特征, 例如聚类数或聚类数。它的大小, 影响分区的质量。

该算法为每次迭代获取数据集的少量随机选择。根据群集质心的先前位置, 将批次中的每个数据分配给群集。然后, 它基于批次中的新点来更新聚类质心的位置。该更新是梯度下降更新, 它比正常更新快得多批量K均值更新.

以下是用于迷你批K均值–

Given a dataset D = {d1, d2, d3, .....dn}, no. of iterations t, batch size b, no. of clusters k.

k clusters C = {c1, c2, c3, ......ck}

initialize k cluster centers O = {o1, o2, .......ok}
# _initialize each cluster
Ci = Φ (1=<i =<k)
# _initialize no. of data in each cluster
Nci = 0 (1=<i =<k)

for j=1 to t do:
    # M is the batch dataset and xm
    # is the sample randomly chosen from D
    M = {xm | 1 =<m =<b}

    # catch cluster center for each
    # sample in the batch data set
    for m=1 to b do:
        oi(xm) = sum(xm)/|c|i (xm ε M and xm ε ci)
    end for
    # update the cluster center with each batch set

     for m=1 to b do:
        # get the cluster center for xm
        oi = oi(xm)
        # update number of data for each cluster center
        Nci = Nci + 1
        #calculate learning rate for each cluster center
        lr=1/Nci
        # take gradient step to update cluster center
        oi = (1-lr)oi + lr*xm
     end for
end for

上述算法的Python实现

scikit学习库：

from sklearn.cluster import MiniBatchKMeans, KMeans
from sklearn.metrics.pairwise import pairwise_distances_argmin
from sklearn.datasets.samples_generator import make_blobs
  
# Load data in X 
batch_size = 45
centers = [[ 1 , 1 ], [ - 2 , - 1 ], [ 1 , - 2 ], [ 1 , 9 ]]
n_clusters = len (centers)
X, labels_true = make_blobs(n_samples = 3000 , centers = centers, cluster_std = 0.9 )
  
# perform the mini batch K-means
mbk = MiniBatchKMeans(init = 'k-means++' , n_clusters = 4 , batch_size = batch_size, n_init = 10 , max_no_improvement = 10 , verbose = 0 )
  
mbk.fit(X)
mbk_means_cluster_centers = np.sort(mbk.cluster_centers_, axis = 0 )
mbk_means_labels = pairwise_distances_argmin(X, mbk_means_cluster_centers)
  
# print the labels of each data
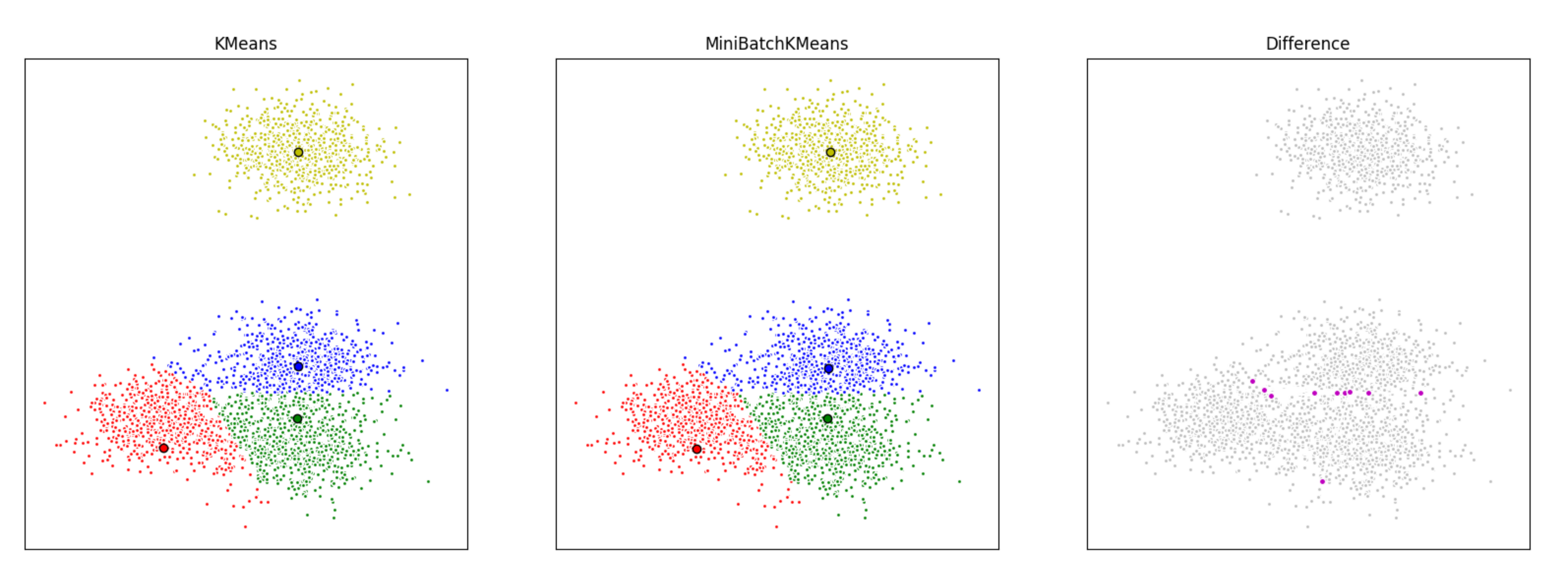
print (mbk_means_labels)

迷你批次K均值更快, 但结果却与普通批次K均值略有不同。

在这里, 我们首先使用K均值, 然后使用小批量K均值对一组数据进行聚类, 然后绘制结果。我们还将绘制在两种算法之间标记不同的点。

随着簇的数量和数据数量的增加, 计算时间的相对节省也增加了。仅在簇数很大的情况下, 节省的计算时间才更加明显。当簇数较大时, 批大小在计算时间中的影响也更加明显。可以得出结论, 增加簇的数量, 会降低小批量K均值解决方案与K均值解决方案的相似性。尽管分区之间的一致性随着群集数量的增加而降低, 但是目标函数并不会以相同的速率退化。这意味着最终分区是不同的, 但是质量更接近。

参考文献：

https://upcommons.upc.edu/bitstream/handle/2117/23414/R13-8.pdf

https://scikit-learn.org/stable/modules/generated/sklearn.cluster.MiniBatchKMeans.html