梯度下降
是机器学习框架中用于训练不同模型的一种优化技术。训练过程由目标函数(或误差函数)组成, 该函数确定机器学习模型在给定数据集上的误差。
在训练时, 该算法的参数被初始化为随机值。随着算法的迭代, 参数被更新, 使得我们越来越接近函数的最佳值。
然而, 自适应优化算法由于其迅速融合的能力而越来越受欢迎。与传统的Gradient Descent相比, 所有这些算法都使用先前迭代的统计数据来增强收敛过程。
基于动量的优化:
一种自适应优化算法, 该算法使用先前迭代中梯度的指数加权平均值来稳定收敛, 从而实现更快的优化。例如, 在大多数现实世界中的深度神经网络应用程序中, 训练都是在嘈杂的数据上进行的。因此, 在优化过程中分批馈送数据时, 有必要减少噪声的影响。这个问题可以用解决指数加权平均值(或指数加权移动平均值)。
实施指数加权平均值:
为了在大小为N的嘈杂数据集中近似趋势:
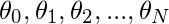
, 我们维护了一组参数
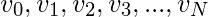
。当我们遍历数据集中的所有值时, 我们计算出如下参数:
On iteration t:
Get next该算法对
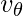
超过先前的值
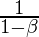
迭代。这种平均可确保仅保留趋势, 并且将噪声平均。该方法在基于动量的梯度下降中用作策略, 以使其对数据样本中的噪声具有鲁棒性, 从而加快了训练速度。
例如, 如果要优化功能
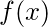
在参数上
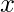
, 以下伪代码说明了该算法:
On iteration t:
On the current batch, compute此优化算法的超参数为
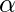
, 称为
学习率
和,
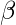
, 类似于力学上的加速。
以下是在函数上基于动量的梯度下降的实现
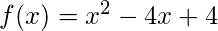
:
import math
# HyperParameters of the optimization algorithm
alpha = 0.01
beta = 0.9
# Objective function
def obj_func(x):
return x * x - 4 * x + 4
# Gradient of the objective function
def grad(x):
return 2 * x - 4
# Parameter of the objective function
x = 0
# Number of iterations
iterations = 0
v = 0
while ( 1 ):
iterations + = 1
v = beta * v + ( 1 - beta) * grad(x)
x_prev = x
x = x - alpha * v
print ( "Value of objective function on iteration" , iterations, "is" , x)
if x_prev = = x:
print ( "Done optimizing the objective function. " )
break
