ML算法：主成分分析（PCA）详细指南

主成分分析(PCA)是一种使用正交变换的统计过程, 该正交变换将一组相关变量转换为一组不相关变量。 PCA是探索性数据分析和预测模型的机器学习中使用最广泛的工具。此外, PCA是一种无监督的统计技术, 用于检查一组变量之间的相互关系。这也称为一般因素分析, 其中回归确定一条最佳拟合线。

所需模块：

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
% matplotlib inline

代码1：

# Here we are using inbuilt dataset of scikit learn
from sklearn.datasets import load_breast_cancer
  
# instantiating
cancer = load_breast_cancer()
  
# creating dataframe
df = pd.DataFrame(cancer[ 'data' ], columns = cancer[ 'feature_names' ])
  
# checking head of dataframe
df.head()

输出如下：

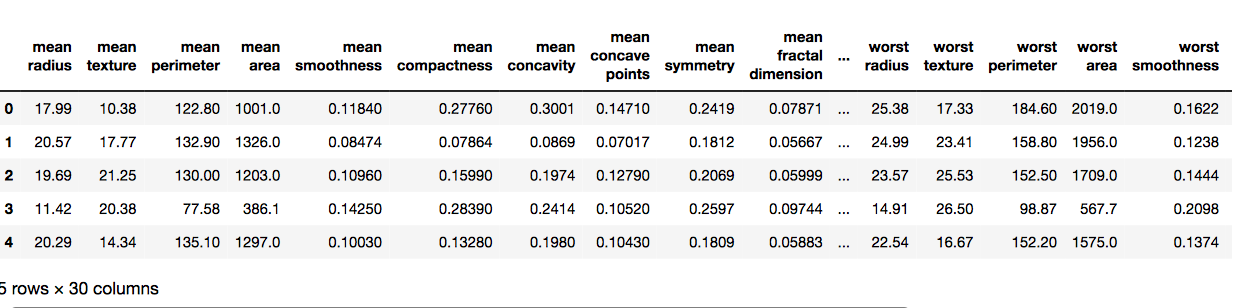
代码2：

# Importing standardscalar module 
from sklearn.preprocessing import StandardScaler
  
scalar = StandardScaler()
  
# fitting
scalar.fit(df)
scaled_data = scalar.transform(df)
  
# Importing PCA
from sklearn.decomposition import PCA
  
# Let's say, components = 2
pca = PCA(n_components = 2 )
pca.fit(scaled_data)
x_pca = pca.transform(scaled_data)
  
x_pca.shape

输出如下：

＃减少至569, 2

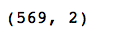
# giving a larger plot
plt.figure(figsize = ( 8 , 6 ))
  
plt.scatter(x_pca[:, 0 ], x_pca[:, 1 ], c = cancer[ 'target' ], cmap = 'plasma' )
  
# labeling x and y axes
plt.xlabel( 'First Principal Component' )
plt.ylabel( 'Second Principal Component' )

输出如下：

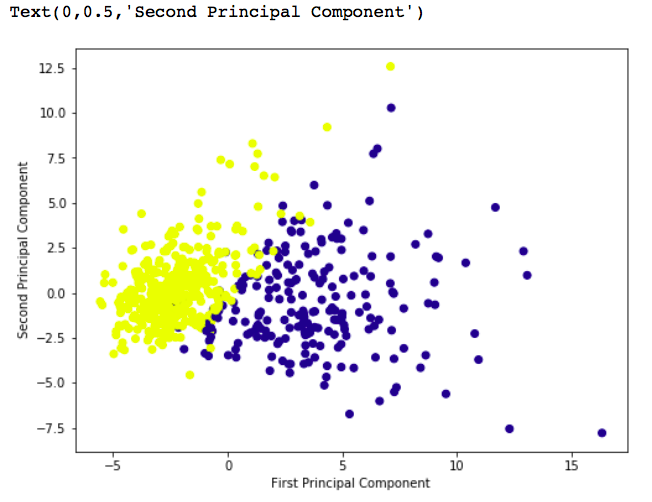
# components
pca.components_

输出如下：

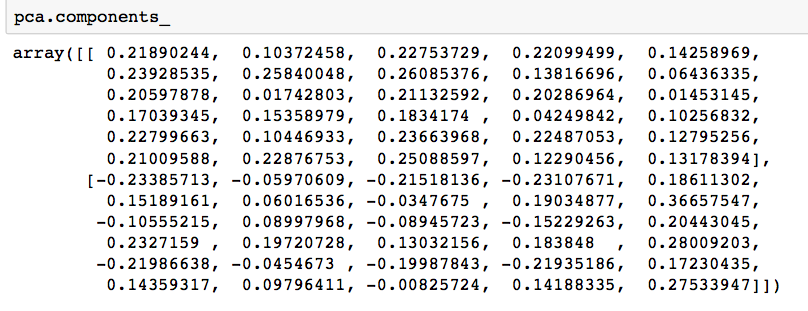
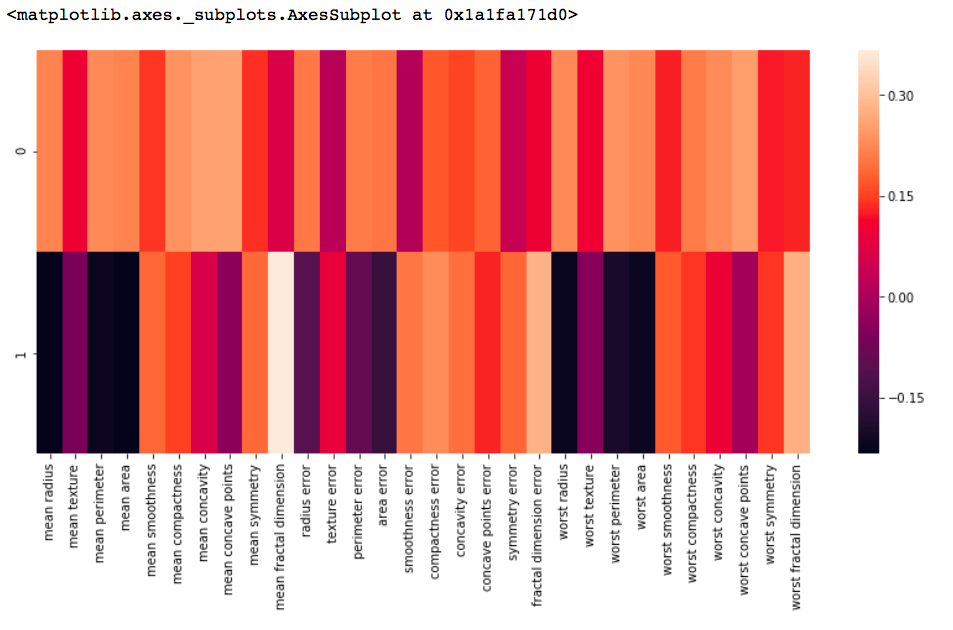
df_comp = pd.DataFrame(pca.components_, columns = cancer[ 'feature_names' ])
  
plt.figure(figsize = ( 14 , 6 ))
  
# plotting heatmap
sns.heatmap(df_comp)

输出如下：

---