什么是梯度下降?
在解释随机梯度下降(SGD)之前, 让我们首先描述什么是梯度下降。梯度下降是机器学习和深度学习中一种流行的优化技术, 它可以与大多数(如果不是全部)学习算法一起使用。梯度是函数的斜率。它测量变量响应于另一个变量的变化的程度。从数学上讲, 梯度下降是一个凸函数, 其输出是其输入的一组参数的偏导数。梯度越大, 斜率越大。
从初始值开始, 迭代运行"梯度下降"以找到参数的最佳值, 以找到给定成本函数的最小可能值。
梯度下降的类型:
通常, 有三种类型的梯度下降:
- 批次梯度下降
- 随机梯度下降
- 小批量梯度下降
在本文中, 我们将讨论随机梯度下降或SGD。
随机梯度下降(SGD):
这个单词 '随机‘是指与随机概率相关的系统或过程。因此, 在随机梯度下降中, 随机选择一些样本, 而不是每次迭代的整个数据集。在"梯度下降"中, 有一个称为"批处理"的术语, 表示来自数据集的样本总数, 用于计算每次迭代的梯度。在典型的"梯度下降"优化中, 例如"批次梯度下降", 该批次被视为整个数据集。尽管使用整个数据集对于以较少的噪声和较少的随机性达到最小值非常有用, 但是当我们的数据集变大时就会出现问题。
假设你的数据集中有一百万个样本, 因此, 如果你使用典型的Gradient Descent优化技术, 则在执行Gradient Descent时必须使用全部一百万个样本来完成一次迭代, 并且必须为每次迭代, 直到达到最小值。因此, 执行起来在计算上变得非常昂贵。
通过随机梯度下降解决了这个问题。在SGD中, 它仅使用单个样本(即, 批大小为1)执行每次迭代。样本随机混洗并选择用于执行迭代。
SGD算法:
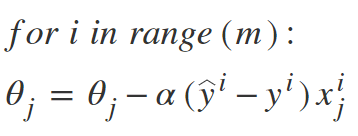
因此, 在SGD中, 我们在每次迭代中找到单个示例的成本函数的梯度, 而不是所有示例的成本函数的梯度之和。
在SGD中, 由于每次迭代仅从数据集中随机选择一个样本, 因此算法所采用的到达最小值的路径通常比典型的Gradient Descent算法更嘈杂。但这没什么大不了的, 因为只要我们达到最小值, 并且训练时间明显缩短, 算法所采用的路径就无关紧要。
批次梯度下降采用的路径–
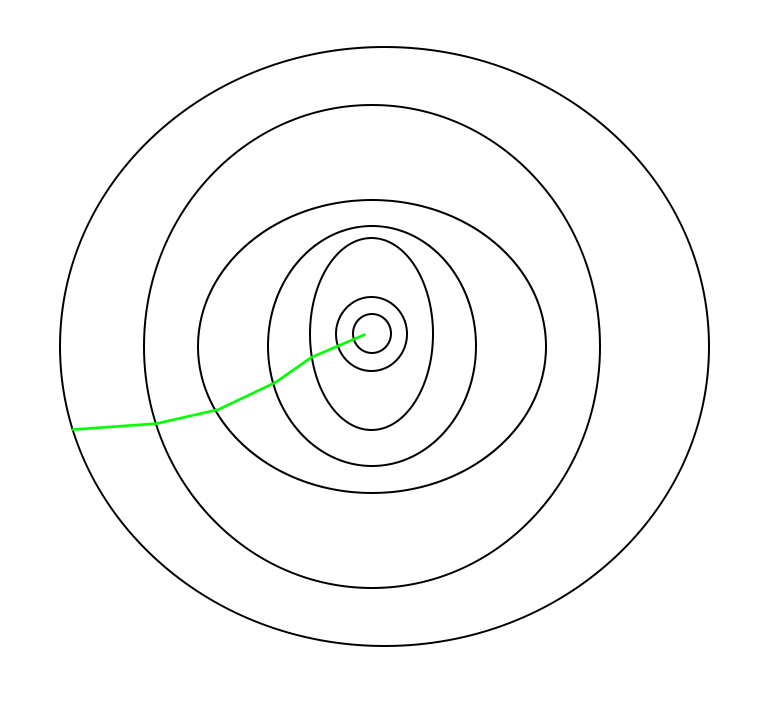
随机梯度下降采取的路径–
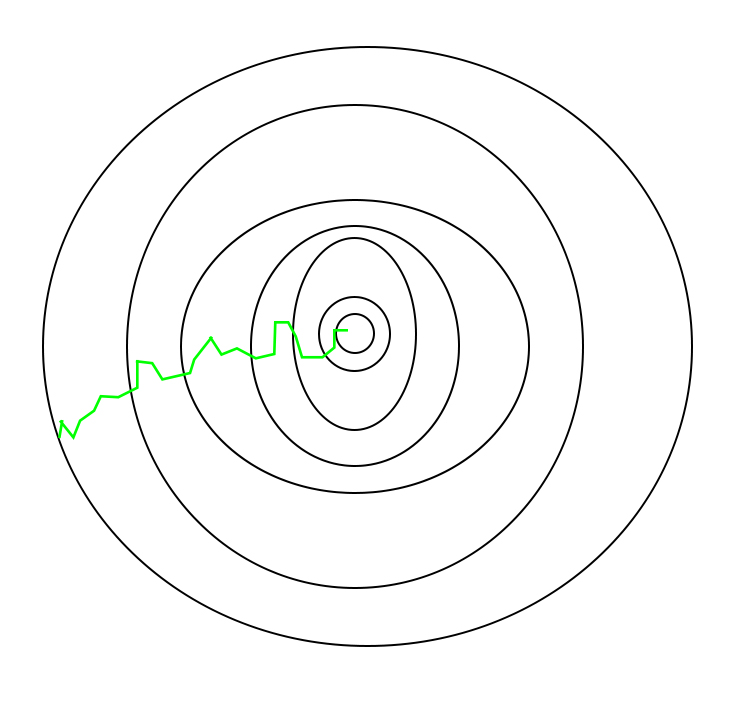
要注意的一件事是, 由于SGD通常比典型的Gradient Descent噪声更大, 因此由于其下降的随机性, 通常需要花费更多的迭代次数才能达到最小值。尽管与典型的梯度下降相比, 它需要更多的迭代次数才能达到最小值, 但在计算上仍比典型的梯度下降便宜得多。因此, 在大多数情况下, SGD优先于批次梯度下降, 以优化学习算法。
Python中SGD的伪代码:
def SGD(f, theta0, alpha, num_iters):
"""
Arguments:
f -- the function to optimize, it takes a single argument
and yield two outputs, a cost and the gradient
with respect to the arguments
theta0 -- the initial point to start SGD from
num_iters -- total iterations to run SGD for
Return:
theta -- the parameter value after SGD finishes
"""
start_iter = 0
theta = theta0
for iter in xrange (start_iter + 1 , num_iters + 1 ):
_, grad = f(theta)
# there is NO dot product ! return theta
theta = theta - (alpha * grad)这种取值并根据不同参数进行调整以减少损失函数的循环称为反向传播.

