ML：T分布随机邻居嵌入（t-SNE）算法

T分布随机邻居嵌入(t-SNE)是一种非线性降维技术, 非常适合在二维或三维的低维空间中嵌入高维数据以进行可视化。

什么是降维？

降维是一种表示2维或3维n维数据(具有许多特征的多维数据)的技术。

降维的一个例子可以作为分类问题来讨论, 即学生是否会踢足球, 因为温度和湿度都取决于一个特征, 因为这两个特征都高度相关。因此, 我们可以减少此类问题中的特征数量。 3-D分类问题可能很难可视化, 而2-D分类问题可以映射到简单的二维空间, 而1-D问题可以映射到简单的线。

t-SNE如何工作？

t-SNE是一种非线性降维算法, 它基于具有特征的数据点的相似性来查找数据中的模式, 将点的相似性计算为点A选择点B作为其邻居的条件概率。

然后, 它试图最小化高维和低维空间中这些条件概率(或相似性)之间的差异, 以实现低维空间中数据点的完美表示。

时空复杂性

该算法计算成对的条件概率, 并尝试最小化在较高和较低维度上的概率差异之和。这涉及许多计算和计算。因此, 该算法需要大量时间和空间来计算。 t-SNE在数据点数量上具有二次时间和空间复杂度。

在MNIST数据集上应用t-SNE

# Importing Necessary Modules.
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.manifold import TSNE
from sklearn.preprocessing import StandardScaler

代码1：读取数据

# Reading the data using pandas  
df = pd.read_csv( 'mnist_train.csv' )
  
# print first five rows of df
print (df.head( 4 )) 
  
# save the labels into a variable l.
l = df[ 'label' ]
  
# Drop the label feature and store the pixel data in d.
d = df.drop( "label" , axis = 1 )

输出如下：

代码2：

数据预处理

# Data-preprocessing: Standardizing the data
from sklearn.preprocessing import StandardScaler
  
standardized_data = StandardScaler().fit_transform(data)
  
print (standardized_data.shape)

输出如下：

代码3：

# TSNE
# Picking the top 1000 points as TSNE
# takes a lot of time for 15K points
data_1000 = standardized_data[ 0 : 1000 , :]
labels_1000 = labels[ 0 : 1000 ]
  
model = TSNE(n_components = 2 , random_state = 0 )
# configuring the parameteres
# the number of components = 2
# default perplexity = 30
# default learning rate = 200
# default Maximum number of iterations
# for the optimization = 1000
  
tsne_data = model.fit_transform(data_1000)
  
  
# creating a new data frame which
# help us in ploting the result data
tsne_data = np.vstack((tsne_data.T, labels_1000)).T
tsne_df = pd.DataFrame(data = tsne_data, columns = ( "Dim_1" , "Dim_2" , "label" ))
  
# Ploting the result of tsne
sn.FacetGrid(tsne_df, hue = "label" , size = 6 ). map (
        plt.scatter, 'Dim_1' , 'Dim_2' ).add_legend()
  
plt.show()

输出如下：

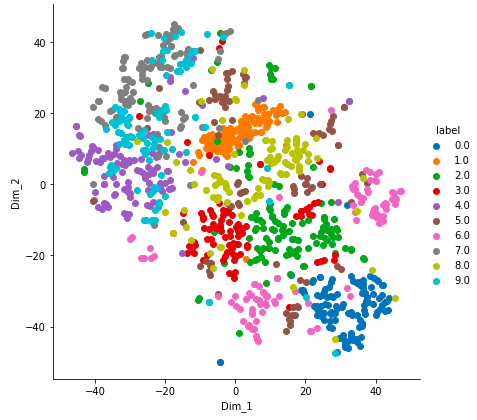
首先, 你的面试准备可通过以下方式增强你的数据结构概念：Python DS课程。

---