先决条件: 支持向量机
超平面和SVM分类器的定义:
对于具有n个特征的线性可分离数据集(因此需要n个维表示), 超平面基本上是一个(n – 1)维子空间, 用于将数据集分为两组, 每个组包含属于不同类的数据点。例如, 对于具有两个特征X和Y(因此位于二维空间中)的数据集, 分离的超平面是一条线(一维子空间)。类似地, 对于具有3维的数据集, 我们具有2维分离的超平面, 依此类推。
在机器学习中, 支持向量机(SVM)是一种非概率的线性二进制分类器, 用于通过学习分离数据的超平面来对数据进行分类。
使用SVM-线性分类器对非线性可分离数据集进行分类:
如上所述, SVM是线性分类器, 它学习(n – 1)维分类器, 用于将数据分类为两类。但是, 它可以用于对非线性数据集进行分类。这可以通过将数据集投影到可以线性分离的更高维度来完成!
为了更好地理解, 让我们考虑圆形数据集。
# importing libraries
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_circles
from mpl_toolkits.mplot3d import Axes3D
# generating data
X, Y = make_circles(n_samples = 500 , noise = 0.02 )
# visualizing data
plt.scatter(X[:, 0 ], X[:, 1 ], c = Y, marker = '.' )
plt.show()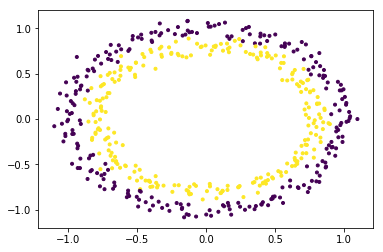
数据集显然是一个非线性数据集, 由两个要素(例如X和Y)组成。
为了使用SVM对数据进行分类, 请引入另一个特征Z = X2+ Y2进入数据集。因此, 将二维数据投影到3维空间中。第一维表示特征X, 第二维表示Y, 第三维表示Z(在数学上等于点(x, y)所在的圆的半径)。现在, 很明显, 对于上面显示的数据, "黄色"数据点属于较小半径的圆, 而"紫色"数据点属于较大半径的圆。因此, 数据沿Z轴可线性分离。
# adding a new dimension to X
X1 = X[:, 0 ].reshape(( - 1 , 1 ))
X2 = X[:, 1 ].reshape(( - 1 , 1 ))
X3 = (X1 * * 2 + X2 * * 2 )
X = np.hstack((X, X3))
# visualizing data in higher dimension
fig = plt.figure()
axes = fig.add_subplot( 111 , projection = '3d' )
axes.scatter(X1, X2, X1 * * 2 + X2 * * 2 , c = Y, depthshade = True )
plt.show()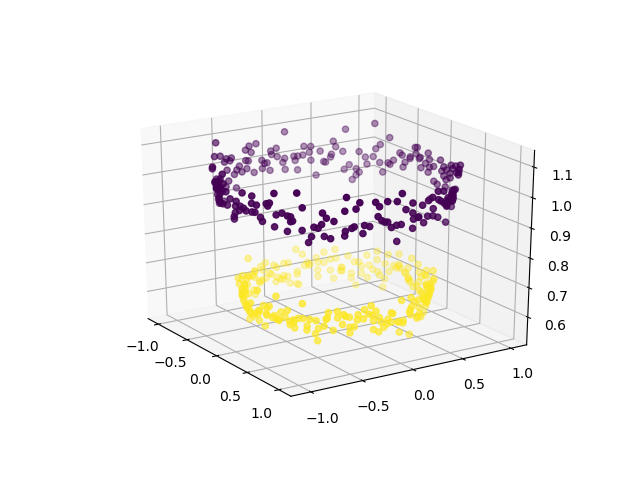
现在, 我们可以使用SVM(或其他任何线性分类器)来学习二维分离超平面。这是超平面的外观:
# create support vector classifier using a linear kernel
from sklearn import svm
svc = svm.SVC(kernel = 'linear' )
svc.fit(X, Y)
w = svc.coef_
b = svc.intercept_
# plotting the separating hyperplane
x1 = X[:, 0 ].reshape(( - 1 , 1 ))
x2 = X[:, 1 ].reshape(( - 1 , 1 ))
x1, x2 = np.meshgrid(x1, x2)
x3 = - (w[ 0 ][ 0 ] * x1 + w[ 0 ][ 1 ] * x2 + b) /w[ 0 ][ 2 ]
fig = plt.figure()
axes2 = fig.add_subplot( 111 , projection = '3d' )
axes2.scatter(X1, X2, X1 * * 2 + X2 * * 2 , c = Y, depthshade = True )
axes1 = fig.gca(projection = '3d' )
axes1.plot_surface(x1, x2, x3, alpha = 0.01 )
plt.show()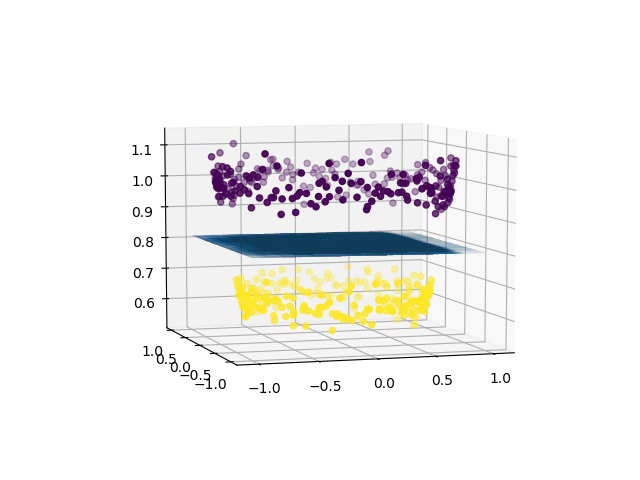
因此, 使用线性分类器, 我们可以分离非线性可分离的数据集。
机器学习中的内核简介:
在机器学习中, 一种称为"内核技巧"的技巧用于学习线性分类器以对非线性数据集进行分类。通过将其投影到更高的维度, 它将线性不可分离的数据转换为线性可分离的数据。将内核函数应用于每个数据实例, 以将原始非线性数据点映射到某个更高维度的空间中, 在这些空间中它们可以线性分离。

![从字法上最小长度N的排列,使得对于正好为K个索引,a[i] a[i]+1](https://www.lsbin.com/wp-content/themes/begin%20lts/img/loading.png)