ML为什么要在分类中进行逻辑回归？

使用线性回归, 所有> = 0.5的预测都可以被视为1, 而其余所有<0.5的预测都可以被视为0。但是随后出现了一个问题, 为什么不能使用它进行分类？

问题–

假设我们将邮件分类为垃圾邮件或非垃圾邮件, 并且我们的输出为ÿ, 可以是0(垃圾邮件)或1(非垃圾邮件)。在线性回归的情况下, hθ(x)可以> 1或<0。尽管我们的预测应该在0到1之间, 但是模型将预测超出范围的值, 即> 1或<0。

因此, 这就是为什么要执行"分类"任务的原因, 即逻辑/乙状结肠回归。

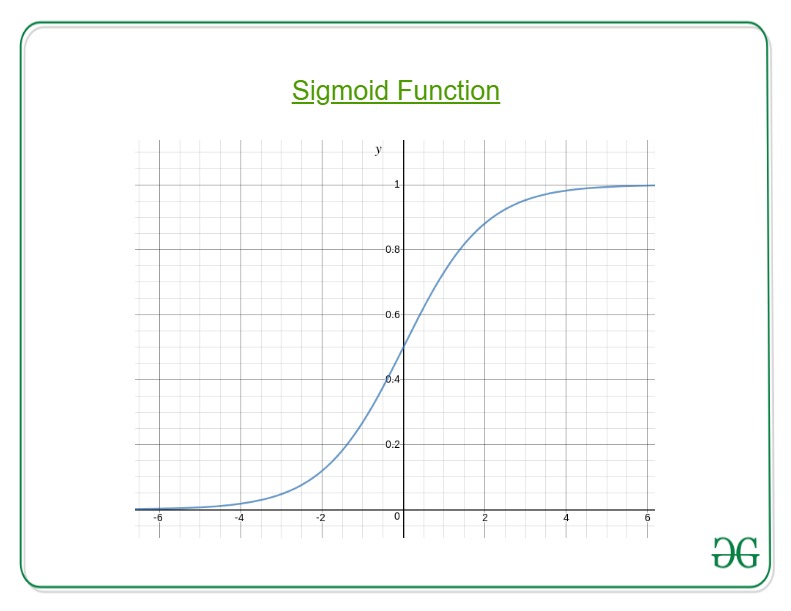
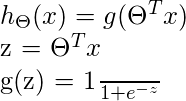
在这里, 我们插入θŤX转化为逻辑函数, 其中θ是权重/参数, X是输入和Hθ(X)是假设函数。G()是S型函数。

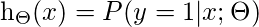
这意味着x参数化为时y = 1的概率θ

为了获得离散值0或1进行分类, 定义了离散边界。假设功能可以翻译为

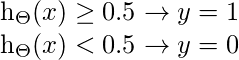
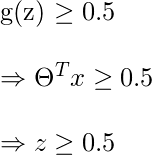
决策边界是区分y = 0和y = 1区域的线。这些决策边界来自所考虑的假设函数。

通过示例了解决策边界–

让我们的假设函数为

然后决策边界看起来像

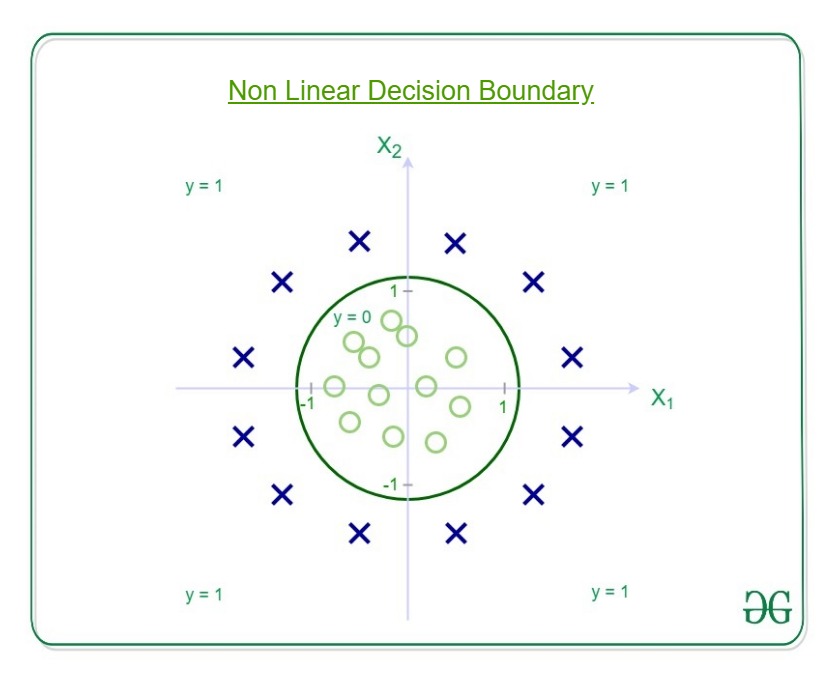
给出权重或参数为–

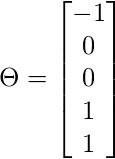
因此, 如果y = 1

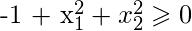
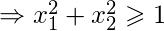
那就是半径为1且原点为中心的圆的方程。这是我们定义的假设的决策边界。

首先, 你的面试准备可通过以下方式增强你的数据结构概念：Python DS课程。

---