本文概述
给定移动数字小键盘。你只能按向上, 向左, 向右或向下按当前按钮。你不允许按底行的角按钮(即*和#)。
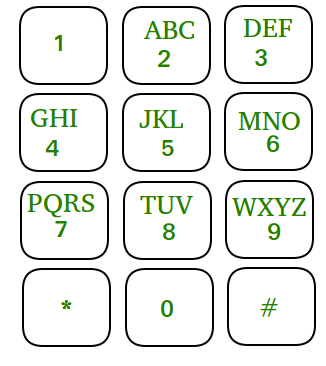
给定数字N, 找出给定长度的可能数字。
例子:
对于N = 1, 可能的数量为10(0、1、2、3, ...., 9)
对于N = 2, 可能的数量为36
可能的数字:00, 08 11, 12, 14 22, 21, 23, 25, 依此类推。
如果我们以0开头, 则有效数字将为00、08(计数:2)
如果我们从1开始, 有效数字将是11、12、14(计数:3)
如果我们从2开始, 有效数字将是22、21、23.25(计数:4)
如果我们以3开头, 则有效数字将为33、32、36(计数:3)
如果我们从4开始, 有效数字将是44, 41, 45, 47(计数:4)
如果我们从5开始, 有效数字将是55、54、52、56、58(计数:5)
………………………………
………………………………
我们需要打印可能的数字。
N = 1是微不足道的情况, 可能的数量为10(0, 1, 2, 3, …。, 9)
对于N> 1, 我们需要从某个按钮开始, 然后移至四个方向(向上, 向左, 向右或向下)中的任意一个, 然后转到一个有效按钮(不应转到*, #)。继续执行此操作, 直到获得N个长度数字(深度优先遍历)。
递归解决方案:
移动键盘是4X3的矩形网格(4行3列)
假设Count(i, j, N)代表从位置(i, j)开始的N个长度数字的计数
If N = 1
Count(i, j, N) = 10
Else
Count(i, j, N) = Sum of all Count(r, c, N-1) where (r, c) is new
position after valid move of length 1 from current
position (i, j)以下是上述递归公式的实现。
C ++
//A Naive Recursive C program to count number of possible numbers
//of given length
#include <stdio.h>
//left, up, right, down move from current location
int row[] = {0, 0, -1, 0, 1};
int col[] = {0, -1, 0, 1, 0};
//Returns count of numbers of length n starting from key position
//(i, j) in a numeric keyboard.
int getCountUtil( char keypad[][3], int i, int j, int n)
{
if (keypad == NULL || n <= 0)
return 0;
//From a given key, only one number is possible of length 1
if (n == 1)
return 1;
int k=0, move=0, ro=0, co=0, totalCount = 0;
//move left, up, right, down from current location and if
//new location is valid, then get number count of length
//(n-1) from that new position and add in count obtained so far
for (move=0; move<5; move++)
{
ro = i + row[move];
co = j + col[move];
if (ro>= 0 && ro <= 3 && co>=0 && co <= 2 &&
keypad[ro][co] != '*' && keypad[ro][co] != '#' )
{
totalCount += getCountUtil(keypad, ro, co, n-1);
}
}
return totalCount;
}
//Return count of all possible numbers of length n
//in a given numeric keyboard
int getCount( char keypad[][3], int n)
{
//Base cases
if (keypad == NULL || n <= 0)
return 0;
if (n == 1)
return 10;
int i=0, j=0, totalCount = 0;
for (i=0; i<4; i++) //Loop on keypad row
{
for (j=0; j<3; j++) //Loop on keypad column
{
//Process for 0 to 9 digits
if (keypad[i][j] != '*' && keypad[i][j] != '#' )
{
//Get count when number is starting from key
//position (i, j) and add in count obtained so far
totalCount += getCountUtil(keypad, i, j, n);
}
}
}
return totalCount;
}
//Driver program to test above function
int main( int argc, char *argv[])
{
char keypad[4][3] = {{ '1' , '2' , '3' }, { '4' , '5' , '6' }, { '7' , '8' , '9' }, { '*' , '0' , '#' }};
printf ( "Count for numbers of length %d: %dn" , 1, getCount(keypad, 1));
printf ( "Count for numbers of length %d: %dn" , 2, getCount(keypad, 2));
printf ( "Count for numbers of length %d: %dn" , 3, getCount(keypad, 3));
printf ( "Count for numbers of length %d: %dn" , 4, getCount(keypad, 4));
printf ( "Count for numbers of length %d: %dn" , 5, getCount(keypad, 5));
return 0;
}Java
//A Naive Recursive Java program
//to count number of possible
//numbers of given length
class GfG
{
//left, up, right, down
//move from current location
static int row[] = { 0 , 0 , - 1 , 0 , 1 };
static int col[] = { 0 , - 1 , 0 , 1 , 0 };
//Returns count of numbers of length
//n starting from key position
//(i, j) in a numeric keyboard.
static int getCountUtil( char keypad[][], int i, int j, int n)
{
if (keypad == null || n <= 0 )
return 0 ;
//From a given key, only one
//number is possible of length 1
if (n == 1 )
return 1 ;
int k = 0 , move = 0 , ro = 0 , co = 0 , totalCount = 0 ;
//move left, up, right, down
//from current location and if
//new location is valid, then
//get number count of length
//(n-1) from that new position
//and add in count obtained so far
for (move= 0 ; move<5 ; move++)
{
ro = i + row[move];
co = j + col[move];
if (ro>= 0 && ro <= 3 && co>= 0 && co <= 2 &&
keypad[ro][co] != '*' && keypad[ro][co] != '#' )
{
totalCount += getCountUtil(keypad, ro, co, n - 1 );
}
}
return totalCount;
}
//Return count of all possible numbers of length n
//in a given numeric keyboard
static int getCount( char keypad[][], int n)
{
//Base cases
if (keypad == null || n <= 0 )
return 0 ;
if (n == 1 )
return 10 ;
int i = 0 , j = 0 , totalCount = 0 ;
for (i = 0 ; i <4 ; i++) //Loop on keypad row
{
for (j= 0 ; j<3 ; j++) //Loop on keypad column
{
//Process for 0 to 9 digits
if (keypad[i][j] != '*' && keypad[i][j] != '#' )
{
//Get count when number is starting from key
//position (i, j) and add in count obtained so far
totalCount += getCountUtil(keypad, i, j, n);
}
}
}
return totalCount;
}
//Driver code
public static void main(String[] args)
{
char keypad[][] = {{ '1' , '2' , '3' }, { '4' , '5' , '6' }, { '7' , '8' , '9' }, { '*' , '0' , '#' }};
System.out.printf( "Count for numbers of" +
" length %d: %d" , 1 , getCount(keypad, 1 ));
System.out.printf( "\nCount for numbers of" +
"length %d: %d" , 2 , getCount(keypad, 2 ));
System.out.printf( "\nCount for numbers of" +
"length %d: %d" , 3 , getCount(keypad, 3 ));
System.out.printf( "\nCount for numbers of" +
"length %d: %d" , 4 , getCount(keypad, 4 ));
System.out.printf( "\nCount for numbers of" +
"length %d: %d" , 5 , getCount(keypad, 5 ));
}
}
//This code has been contributed by 29AjayKumarC#
//A Naive Recursive C# program
//to count number of possible
//numbers of given length
using System;
class GfG
{
//left, up, right, down
//move from current location
static int []row = {0, 0, -1, 0, 1};
static int []col = {0, -1, 0, 1, 0};
//Returns count of numbers of length
//n starting from key position
//(i, j) in a numeric keyboard.
static int getCountUtil( char [, ]keypad, int i, int j, int n)
{
if (keypad == null || n <= 0)
return 0;
//From a given key, only one
//number is possible of length 1
if (n == 1)
return 1;
int k = 0, move = 0, ro = 0, co = 0, totalCount = 0;
//move left, up, right, down
//from current location and if
//new location is valid, then
//get number count of length
//(n-1) from that new position
//and add in count obtained so far
for (move=0; move<5; move++)
{
ro = i + row[move];
co = j + col[move];
if (ro>= 0 && ro <= 3 && co>=0 && co <= 2 &&
keypad[ro, co] != '*' && keypad[ro, co] != '#' )
{
totalCount += getCountUtil(keypad, ro, co, n - 1);
}
}
return totalCount;
}
//Return count of all possible numbers of length n
//in a given numeric keyboard
static int getCount( char [, ]keypad, int n)
{
//Base cases
if (keypad == null || n <= 0)
return 0;
if (n == 1)
return 10;
int i = 0, j = 0, totalCount = 0;
for (i = 0; i <4; i++) //Loop on keypad row
{
for (j = 0; j <3; j++) //Loop on keypad column
{
//Process for 0 to 9 digits
if (keypad[i, j] != '*' && keypad[i, j] != '#' )
{
//Get count when number is starting from key
//position (i, j) and add in count obtained so far
totalCount += getCountUtil(keypad, i, j, n);
}
}
}
return totalCount;
}
//Driver code
public static void Main()
{
char [, ]keypad = {{ '1' , '2' , '3' }, { '4' , '5' , '6' }, { '7' , '8' , '9' }, { '*' , '0' , '#' }};
Console.Write( "Count for numbers of" +
" length {0}: {1}" , 1, getCount(keypad, 1));
Console.Write( "\nCount for numbers of" +
"length {0}: {1}" , 2, getCount(keypad, 2));
Console.Write( "\nCount for numbers of" +
"length {0}: {1}" , 3, getCount(keypad, 3));
Console.Write( "\nCount for numbers of" +
"length {0}: {1}" , 4, getCount(keypad, 4));
Console.Write( "\nCount for numbers of" +
"length {0}: {1}" , 5, getCount(keypad, 5));
}
}
/* This code contributed by PrinciRaj1992 */的PHP
<?php
//A Naive Recursive PHP program
//to count number of possible
//numbers of given length
//left, up, right, down
//move from current location
//static $row = array(0, 0, -1, 0, 1);
//static $col = array(0, -1, 0, 1, 0);
//Returns count of numbers of length
//n starting from key position
//(i, j) in a numeric keyboard.
function getCountUtil( $keypad , $i , $j , $n )
{
static $row = array (0, 0, -1, 0, 1);
static $col = array (0, -1, 0, 1, 0);
if ( $keypad == null || $n <= 0)
return 0;
//From a given key, only one
//number is possible of length 1
if ( $n == 1)
return 1;
$k = 0; $move = 0; $ro = 0; $co = 0; $totalCount = 0;
//move left, up, right, down
//from current location and if
//new location is valid, then
//get number count of length
//(n-1) from that new position
//and add in count obtained so far
for ( $move = 0; $move <5; $move ++)
{
$ro = $i + $row [ $move ];
$co = $j + $col [ $move ];
if ( $ro>= 0 && $ro <= 3 && $co>=0 && $co <= 2 &&
$keypad [ $ro ][ $co ] != '*' && $keypad [ $ro ][ $co ] != '#' )
{
$totalCount += getCountUtil( $keypad , $ro , $co , $n - 1);
}
}
return $totalCount ;
}
//Return count of all possible numbers of length n
//in a given numeric keyboard
function getCount( $keypad , $n )
{
//Base cases
if ( $keypad == null || $n <= 0)
return 0;
if ( $n == 1)
return 10;
$i = 0; $j = 0; $totalCount = 0;
for ( $i = 0; $i <4; $i ++) //Loop on keypad row
{
for ( $j = 0; $j <3; $j ++) //Loop on keypad column
{
//Process for 0 to 9 digits
if ( $keypad [ $i ][ $j ] != '*' && $keypad [ $i ][ $j ] != '#' )
{
//Get count when number is starting from key
//position (i, j) and add in count obtained so far
$totalCount += getCountUtil( $keypad , $i , $j , $n );
}
}
}
return $totalCount ;
}
//Driver code
{
$keypad = array ( array ( '1' , '2' , '3' ), array ( '4' , '5' , '6' ), array ( '7' , '8' , '9' ), array ( '*' , '0' , '#' ));
echo ( "Count for numbers of" . " length" . getCount( $keypad , 1));
echo ( "\nCount for numbers of" .
" length " . getCount( $keypad , 2));
echo ( "\nCount for numbers of" .
" length " .getCount( $keypad , 3));
echo ( "\nCount for numbers of" .
" length " .getCount( $keypad , 4));
echo ( "\nCount for numbers of" .
" length " .getCount( $keypad , 5));
}
//This code has been contributed by Code_Mech.输出如下:
Count for numbers of length 1: 10
Count for numbers of length 2: 36
Count for numbers of length 3: 138
Count for numbers of length 4: 532
Count for numbers of length 5: 2062动态编程
在较小的路径上有许多重复遍历(对于较小的N而言遍历)以找到所有可能的较长的路径(对于较大的N而言遍历)。例如, 请参见以下两个图。在此遍历中, 对于从两个起始位置(按钮" 4"和" 8")开始的N = 4, 我们可以看到对于N = 2的重复遍历很少(例如4-> 1, 6-> 3, 8-> 9、8-> 7等)。
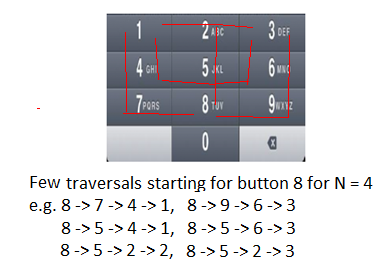
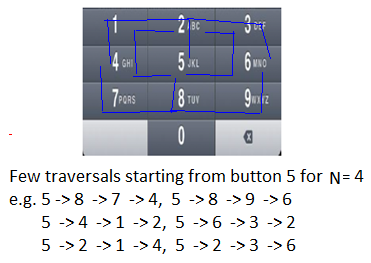
由于问题具有两个属性:最佳子结构和重叠子问题, 可以使用动态编程有效解决。
以下是用于动态编程实现的程序。
C ++
//A Dynamic Programming based C program to count number of
//possible numbers of given length
#include <stdio.h>
//Return count of all possible numbers of length n
//in a given numeric keyboard
int getCount( char keypad[][3], int n)
{
if (keypad == NULL || n <= 0)
return 0;
if (n == 1)
return 10;
//left, up, right, down move from current location
int row[] = {0, 0, -1, 0, 1};
int col[] = {0, -1, 0, 1, 0};
//taking n+1 for simplicity - count[i][j] will store
//number count starting with digit i and length j
int count[10][n+1];
int i=0, j=0, k=0, move=0, ro=0, co=0, num = 0;
int nextNum=0, totalCount = 0;
//count numbers starting with digit i and of lengths 0 and 1
for (i=0; i<=9; i++)
{
count[i][0] = 0;
count[i][1] = 1;
}
//Bottom up - Get number count of length 2, 3, 4, ... , n
for (k=2; k<=n; k++)
{
for (i=0; i<4; i++) //Loop on keypad row
{
for (j=0; j<3; j++) //Loop on keypad column
{
//Process for 0 to 9 digits
if (keypad[i][j] != '*' && keypad[i][j] != '#' )
{
//Here we are counting the numbers starting with
//digit keypad[i][j] and of length k keypad[i][j]
//will become 1st digit, and we need to look for
//(k-1) more digits
num = keypad[i][j] - '0' ;
count[num][k] = 0;
//move left, up, right, down from current location
//and if new location is valid, then get number
//count of length (k-1) from that new digit and
//add in count we found so far
for (move=0; move<5; move++)
{
ro = i + row[move];
co = j + col[move];
if (ro>= 0 && ro <= 3 && co>=0 && co <= 2 &&
keypad[ro][co] != '*' && keypad[ro][co] != '#' )
{
nextNum = keypad[ro][co] - '0' ;
count[num][k] += count[nextNum][k-1];
}
}
}
}
}
}
//Get count of all possible numbers of length "n" starting
//with digit 0, 1, 2, ..., 9
totalCount = 0;
for (i=0; i<=9; i++)
totalCount += count[i][n];
return totalCount;
}
//Driver program to test above function
int main( int argc, char *argv[])
{
char keypad[4][3] = {{ '1' , '2' , '3' }, { '4' , '5' , '6' }, { '7' , '8' , '9' }, { '*' , '0' , '#' }};
printf ( "Count for numbers of length %d: %dn" , 1, getCount(keypad, 1));
printf ( "Count for numbers of length %d: %dn" , 2, getCount(keypad, 2));
printf ( "Count for numbers of length %d: %dn" , 3, getCount(keypad, 3));
printf ( "Count for numbers of length %d: %dn" , 4, getCount(keypad, 4));
printf ( "Count for numbers of length %d: %dn" , 5, getCount(keypad, 5));
return 0;
}Java
//A Dynamic Programming based Java program to
//count number of possible numbers of given length
class GFG
{
//Return count of all possible numbers of length n
//in a given numeric keyboard
static int getCount( char keypad[][], int n)
{
if (keypad == null || n <= 0 )
return 0 ;
if (n == 1 )
return 10 ;
//left, up, right, down move from current location
int row[] = { 0 , 0 , - 1 , 0 , 1 };
int col[] = { 0 , - 1 , 0 , 1 , 0 };
//taking n+1 for simplicity - count[i][j] will store
//number count starting with digit i and length j
int [][]count = new int [ 10 ][n + 1 ];
int i = 0 , j = 0 , k = 0 , move = 0 , ro = 0 , co = 0 , num = 0 ;
int nextNum = 0 , totalCount = 0 ;
//count numbers starting with digit i
//and of lengths 0 and 1
for (i = 0 ; i <= 9 ; i++)
{
count[i][ 0 ] = 0 ;
count[i][ 1 ] = 1 ;
}
//Bottom up - Get number count of length 2, 3, 4, ... , n
for (k = 2 ; k <= n; k++)
{
for (i = 0 ; i <4 ; i++) //Loop on keypad row
{
for (j = 0 ; j <3 ; j++) //Loop on keypad column
{
//Process for 0 to 9 digits
if (keypad[i][j] != '*' &&
keypad[i][j] != '#' )
{
//Here we are counting the numbers starting with
//digit keypad[i][j] and of length k keypad[i][j]
//will become 1st digit, and we need to look for
//(k-1) more digits
num = keypad[i][j] - '0' ;
count[num][k] = 0 ;
//move left, up, right, down from current location
//and if new location is valid, then get number
//count of length (k-1) from that new digit and
//add in count we found so far
for (move = 0 ; move <5 ; move++)
{
ro = i + row[move];
co = j + col[move];
if (ro>= 0 && ro <= 3 && co>= 0 &&
co <= 2 && keypad[ro][co] != '*' &&
keypad[ro][co] != '#' )
{
nextNum = keypad[ro][co] - '0' ;
count[num][k] += count[nextNum][k - 1 ];
}
}
}
}
}
}
//Get count of all possible numbers of length "n"
//starting with digit 0, 1, 2, ..., 9
totalCount = 0 ;
for (i = 0 ; i <= 9 ; i++)
totalCount += count[i][n];
return totalCount;
}
//Driver Code
public static void main(String[] args)
{
char keypad[][] = {{ '1' , '2' , '3' }, { '4' , '5' , '6' }, { '7' , '8' , '9' }, { '*' , '0' , '#' }};
System.out.printf( "Count for numbers of length %d: %d\n" , 1 , getCount(keypad, 1 ));
System.out.printf( "Count for numbers of length %d: %d\n" , 2 , getCount(keypad, 2 ));
System.out.printf( "Count for numbers of length %d: %d\n" , 3 , getCount(keypad, 3 ));
System.out.printf( "Count for numbers of length %d: %d\n" , 4 , getCount(keypad, 4 ));
System.out.printf( "Count for numbers of length %d: %d\n" , 5 , getCount(keypad, 5 ));
}
}
//This code is contributed by Rajput-JiC#
//A Dynamic Programming based C# program to
//count number of possible numbers of given Length
using System;
class GFG
{
//Return count of all possible numbers of Length n
//in a given numeric keyboard
static int getCount( char [, ]keypad, int n)
{
if (keypad == null || n <= 0)
return 0;
if (n == 1)
return 10;
//left, up, right, down move
//from current location
int []row = {0, 0, -1, 0, 1};
int []col = {0, -1, 0, 1, 0};
//taking n+1 for simplicity - count[i, j]
//will store number count starting with
//digit i and.Length j
int [, ]count = new int [10, n + 1];
int i = 0, j = 0, k = 0, move = 0, ro = 0, co = 0, num = 0;
int nextNum = 0, totalCount = 0;
//count numbers starting with digit i
//and of.Lengths 0 and 1
for (i = 0; i <= 9; i++)
{
count[i, 0] = 0;
count[i, 1] = 1;
}
//Bottom up - Get number count of
//Length 2, 3, 4, ... , n
for (k = 2; k <= n; k++)
{
for (i = 0; i <4; i++) //Loop on keypad row
{
for (j = 0; j <3; j++) //Loop on keypad column
{
//Process for 0 to 9 digits
if (keypad[i, j] != '*' &&
keypad[i, j] != '#' )
{
//Here we are counting the numbers starting with
//digit keypad[i, j] and of.Length k keypad[i, j]
//will become 1st digit, and we need to look for
//(k-1) more digits
num = keypad[i, j] - '0' ;
count[num, k] = 0;
//move left, up, right, down from current location
//and if new location is valid, then get number
//count of.Length (k-1) from that new digit and
//.Add in count we found so far
for (move = 0; move <5; move++)
{
ro = i + row[move];
co = j + col[move];
if (ro>= 0 && ro <= 3 && co>= 0 &&
co <= 2 && keypad[ro, co] != '*' &&
keypad[ro, co] != '#' )
{
nextNum = keypad[ro, co] - '0' ;
count[num, k] += count[nextNum, k - 1];
}
}
}
}
}
}
//Get count of all possible numbers of.Length "n"
//starting with digit 0, 1, 2, ..., 9
totalCount = 0;
for (i = 0; i <= 9; i++)
totalCount += count[i, n];
return totalCount;
}
//Driver Code
public static void Main(String[] args)
{
char [, ]keypad = {{ '1' , '2' , '3' }, { '4' , '5' , '6' }, { '7' , '8' , '9' }, { '*' , '0' , '#' }};
Console.Write( "Count for numbers of.Length {0}: {1}\n" , 1, getCount(keypad, 1));
Console.Write( "Count for numbers of.Length {0}: {1}\n" , 2, getCount(keypad, 2));
Console.Write( "Count for numbers of.Length {0}: {1}\n" , 3, getCount(keypad, 3));
Console.Write( "Count for numbers of.Length {0}: {1}\n" , 4, getCount(keypad, 4));
Console.Write( "Count for numbers of.Length {0}: {1}\n" , 5, getCount(keypad, 5));
}
}
//This code is contributed by Rajput-Ji输出如下:
Count for numbers of length 1: 10
Count for numbers of length 2: 36
Count for numbers of length 3: 138
Count for numbers of length 4: 532
Count for numbers of length 5: 2062空间优化的解决方案:
上述动态编程方法也需要O(n)时间运行, 并且需要O(n)辅助空间, 因为只有一个for循环运行n次, 其他for循环运行恒定时间。我们可以看到第n次迭代仅需要第(n-1)次迭代中的数据, 因此我们不需要保留较旧迭代中的数据。我们可以使用只有两个大小为10的数组的高效空间动态编程方法。感谢Nik提出了这种解决方案。
C ++
//A Space Optimized C program to count number of possible numbers
//of given length
#include <stdio.h>
//Return count of all possible numbers of length n
//in a given numeric keyboard
int getCount( char keypad[][3], int n)
{
if (keypad == NULL || n <= 0)
return 0;
if (n == 1)
return 10;
//odd[i], even[i] arrays represent count of numbers starting
//with digit i for any length j
int odd[10], even[10];
int i = 0, j = 0, useOdd = 0, totalCount = 0;
for (i=0; i<=9; i++)
odd[i] = 1; //for j = 1
for (j=2; j<=n; j++) //Bottom Up calculation from j = 2 to n
{
useOdd = 1 - useOdd;
//Here we are explicitly writing lines for each number 0
//to 9. But it can always be written as DFS on 4X3 grid
//using row, column array valid moves
if (useOdd == 1)
{
even[0] = odd[0] + odd[8];
even[1] = odd[1] + odd[2] + odd[4];
even[2] = odd[2] + odd[1] + odd[3] + odd[5];
even[3] = odd[3] + odd[2] + odd[6];
even[4] = odd[4] + odd[1] + odd[5] + odd[7];
even[5] = odd[5] + odd[2] + odd[4] + odd[8] + odd[6];
even[6] = odd[6] + odd[3] + odd[5] + odd[9];
even[7] = odd[7] + odd[4] + odd[8];
even[8] = odd[8] + odd[0] + odd[5] + odd[7] + odd[9];
even[9] = odd[9] + odd[6] + odd[8];
}
else
{
odd[0] = even[0] + even[8];
odd[1] = even[1] + even[2] + even[4];
odd[2] = even[2] + even[1] + even[3] + even[5];
odd[3] = even[3] + even[2] + even[6];
odd[4] = even[4] + even[1] + even[5] + even[7];
odd[5] = even[5] + even[2] + even[4] + even[8] + even[6];
odd[6] = even[6] + even[3] + even[5] + even[9];
odd[7] = even[7] + even[4] + even[8];
odd[8] = even[8] + even[0] + even[5] + even[7] + even[9];
odd[9] = even[9] + even[6] + even[8];
}
}
//Get count of all possible numbers of length "n" starting
//with digit 0, 1, 2, ..., 9
totalCount = 0;
if (useOdd == 1)
{
for (i=0; i<=9; i++)
totalCount += even[i];
}
else
{
for (i=0; i<=9; i++)
totalCount += odd[i];
}
return totalCount;
}
//Driver program to test above function
int main()
{
char keypad[4][3] = {{ '1' , '2' , '3' }, { '4' , '5' , '6' }, { '7' , '8' , '9' }, { '*' , '0' , '#' }
};
printf ( "Count for numbers of length %d: %dn" , 1, getCount(keypad, 1));
printf ( "Count for numbers of length %d: %dn" , 2, getCount(keypad, 2));
printf ( "Count for numbers of length %d: %dn" , 3, getCount(keypad, 3));
printf ( "Count for numbers of length %d: %dn" , 4, getCount(keypad, 4));
printf ( "Count for numbers of length %d: %dn" , 5, getCount(keypad, 5));
return 0;
}Java
//A Space Optimized Java program to
//count number of possible numbers
//of given length
class GFG
{
//Return count of all possible numbers of
//length n in a given numeric keyboard
static int getCount( char keypad[][], int n)
{
if (keypad == null || n <= 0 )
return 0 ;
if (n == 1 )
return 10 ;
//odd[i], even[i] arrays represent count of
//numbers starting with digit i for any length j
int []odd = new int [ 10 ];
int []even = new int [ 10 ];
int i = 0 , j = 0 , useOdd = 0 , totalCount = 0 ;
for (i = 0 ; i <= 9 ; i++)
odd[i] = 1 ; //for j = 1
//Bottom Up calculation from j = 2 to n
for (j = 2 ; j <= n; j++)
{
useOdd = 1 - useOdd;
//Here we are explicitly writing lines
//for each number 0 to 9. But it can always be
//written as DFS on 4X3 grid using row, //column array valid moves
if (useOdd == 1 )
{
even[ 0 ] = odd[ 0 ] + odd[ 8 ];
even[ 1 ] = odd[ 1 ] + odd[ 2 ] + odd[ 4 ];
even[ 2 ] = odd[ 2 ] + odd[ 1 ] +
odd[ 3 ] + odd[ 5 ];
even[ 3 ] = odd[ 3 ] + odd[ 2 ] + odd[ 6 ];
even[ 4 ] = odd[ 4 ] + odd[ 1 ] +
odd[ 5 ] + odd[ 7 ];
even[ 5 ] = odd[ 5 ] + odd[ 2 ] + odd[ 4 ] +
odd[ 8 ] + odd[ 6 ];
even[ 6 ] = odd[ 6 ] + odd[ 3 ] +
odd[ 5 ] + odd[ 9 ];
even[ 7 ] = odd[ 7 ] + odd[ 4 ] + odd[ 8 ];
even[ 8 ] = odd[ 8 ] + odd[ 0 ] + odd[ 5 ] +
odd[ 7 ] + odd[ 9 ];
even[ 9 ] = odd[ 9 ] + odd[ 6 ] + odd[ 8 ];
}
else
{
odd[ 0 ] = even[ 0 ] + even[ 8 ];
odd[ 1 ] = even[ 1 ] + even[ 2 ] + even[ 4 ];
odd[ 2 ] = even[ 2 ] + even[ 1 ] +
even[ 3 ] + even[ 5 ];
odd[ 3 ] = even[ 3 ] + even[ 2 ] + even[ 6 ];
odd[ 4 ] = even[ 4 ] + even[ 1 ] +
even[ 5 ] + even[ 7 ];
odd[ 5 ] = even[ 5 ] + even[ 2 ] + even[ 4 ] +
even[ 8 ] + even[ 6 ];
odd[ 6 ] = even[ 6 ] + even[ 3 ] +
even[ 5 ] + even[ 9 ];
odd[ 7 ] = even[ 7 ] + even[ 4 ] + even[ 8 ];
odd[ 8 ] = even[ 8 ] + even[ 0 ] + even[ 5 ] +
even[ 7 ] + even[ 9 ];
odd[ 9 ] = even[ 9 ] + even[ 6 ] + even[ 8 ];
}
}
//Get count of all possible numbers of
//length "n" starting with digit 0, 1, 2, ..., 9
totalCount = 0 ;
if (useOdd == 1 )
{
for (i = 0 ; i <= 9 ; i++)
totalCount += even[i];
}
else
{
for (i = 0 ; i <= 9 ; i++)
totalCount += odd[i];
}
return totalCount;
}
//Driver Code
public static void main(String[] args)
{
char keypad[][] = {{ '1' , '2' , '3' }, { '4' , '5' , '6' }, { '7' , '8' , '9' }, { '*' , '0' , '#' }};
System.out.printf( "Count for numbers of length %d: %d\n" , 1 , getCount(keypad, 1 ));
System.out.printf( "Count for numbers of length %d: %d\n" , 2 , getCount(keypad, 2 ));
System.out.printf( "Count for numbers of length %d: %d\n" , 3 , getCount(keypad, 3 ));
System.out.printf( "Count for numbers of length %d: %d\n" , 4 , getCount(keypad, 4 ));
System.out.printf( "Count for numbers of length %d: %d\n" , 5 , getCount(keypad, 5 ));
}
}
//This code is contributed by PrinciRaj1992Python 3
# A Space Optimized Python program to count
# number of possible numbers
# of given length
# Return count of all possible numbers
# of length n
# in a given numeric keyboard
def getCount(keypad, n):
if ( not keypad or n <= 0 ):
return 0
if (n = = 1 ):
return 10
# odd[i], even[i] arrays represent
# count of numbers starting
# with digit i for any length j
odd = [ 0 ] * 10
even = [ 0 ] * 10
i = 0
j = 0
useOdd = 0
totalCount = 0
for i in range ( 10 ):
odd[i] = 1 # for j = 1
for j in range ( 2 , n + 1 ): # Bottom Up calculation from j = 2 to n
useOdd = 1 - useOdd
# Here we are explicitly writing lines for each number 0
# to 9. But it can always be written as DFS on 4X3 grid
# using row, column array valid moves
if (useOdd = = 1 ):
even[ 0 ] = odd[ 0 ] + odd[ 8 ]
even[ 1 ] = odd[ 1 ] + odd[ 2 ] + odd[ 4 ]
even[ 2 ] = odd[ 2 ] + odd[ 1 ] + odd[ 3 ] + odd[ 5 ]
even[ 3 ] = odd[ 3 ] + odd[ 2 ] + odd[ 6 ]
even[ 4 ] = odd[ 4 ] + odd[ 1 ] + odd[ 5 ] + odd[ 7 ]
even[ 5 ] = odd[ 5 ] + odd[ 2 ] + odd[ 4 ] + odd[ 8 ] + odd[ 6 ]
even[ 6 ] = odd[ 6 ] + odd[ 3 ] + odd[ 5 ] + odd[ 9 ]
even[ 7 ] = odd[ 7 ] + odd[ 4 ] + odd[ 8 ]
even[ 8 ] = odd[ 8 ] + odd[ 0 ] + odd[ 5 ] + odd[ 7 ] + odd[ 9 ]
even[ 9 ] = odd[ 9 ] + odd[ 6 ] + odd[ 8 ]
else :
odd[ 0 ] = even[ 0 ] + even[ 8 ]
odd[ 1 ] = even[ 1 ] + even[ 2 ] + even[ 4 ]
odd[ 2 ] = even[ 2 ] + even[ 1 ] + even[ 3 ] + even[ 5 ]
odd[ 3 ] = even[ 3 ] + even[ 2 ] + even[ 6 ]
odd[ 4 ] = even[ 4 ] + even[ 1 ] + even[ 5 ] + even[ 7 ]
odd[ 5 ] = even[ 5 ] + even[ 2 ] + even[ 4 ] + even[ 8 ] + even[ 6 ]
odd[ 6 ] = even[ 6 ] + even[ 3 ] + even[ 5 ] + even[ 9 ]
odd[ 7 ] = even[ 7 ] + even[ 4 ] + even[ 8 ]
odd[ 8 ] = even[ 8 ] + even[ 0 ] + even[ 5 ] + even[ 7 ] + even[ 9 ]
odd[ 9 ] = even[ 9 ] + even[ 6 ] + even[ 8 ]
# Get count of all possible numbers of length "n" starting
# with digit 0, 1, 2, ..., 9
totalCount = 0
if (useOdd = = 1 ):
for i in range ( 10 ):
totalCount + = even[i]
else :
for i in range ( 10 ):
totalCount + = odd[i]
return totalCount
# Driver program to test above function
if __name__ = = "__main__" :
keypad = [[ '1' , '2' , '3' ], [ '4' , '5' , '6' ], [ '7' , '8' , '9' ], [ '*' , '0' , '#' ]]
print ( "Count for numbers of length " , 1 , ": " , getCount(keypad, 1 ))
print ( "Count for numbers of length " , 2 , ": " , getCount(keypad, 2 ))
print ( "Count for numbers of length " , 3 , ": " , getCount(keypad, 3 ))
print ( "Count for numbers of length " , 4 , ": " , getCount(keypad, 4 ))
print ( "Count for numbers of length " , 5 , ": " , getCount(keypad, 5 ))
# This code is contributed by
# ChitraNayalC#
//A Space Optimized C# program to
//count number of possible numbers
//of given length
using System;
class GFG
{
//Return count of all possible numbers of
//length n in a given numeric keyboard
static int getCount( char [, ]keypad, int n)
{
if (keypad == null || n <= 0)
return 0;
if (n == 1)
return 10;
//odd[i], even[i] arrays represent count of
//numbers starting with digit i for any length j
int []odd = new int [10];
int []even = new int [10];
int i = 0, j = 0, useOdd = 0, totalCount = 0;
for (i = 0; i <= 9; i++)
odd[i] = 1; //for j = 1
//Bottom Up calculation from j = 2 to n
for (j = 2; j <= n; j++)
{
useOdd = 1 - useOdd;
//Here we are explicitly writing lines
//for each number 0 to 9. But it can always be
//written as DFS on 4X3 grid using row, //column array valid moves
if (useOdd == 1)
{
even[0] = odd[0] + odd[8];
even[1] = odd[1] + odd[2] + odd[4];
even[2] = odd[2] + odd[1] +
odd[3] + odd[5];
even[3] = odd[3] + odd[2] + odd[6];
even[4] = odd[4] + odd[1] +
odd[5] + odd[7];
even[5] = odd[5] + odd[2] + odd[4] +
odd[8] + odd[6];
even[6] = odd[6] + odd[3] +
odd[5] + odd[9];
even[7] = odd[7] + odd[4] + odd[8];
even[8] = odd[8] + odd[0] + odd[5] +
odd[7] + odd[9];
even[9] = odd[9] + odd[6] + odd[8];
}
else
{
odd[0] = even[0] + even[8];
odd[1] = even[1] + even[2] + even[4];
odd[2] = even[2] + even[1] +
even[3] + even[5];
odd[3] = even[3] + even[2] + even[6];
odd[4] = even[4] + even[1] +
even[5] + even[7];
odd[5] = even[5] + even[2] + even[4] +
even[8] + even[6];
odd[6] = even[6] + even[3] +
even[5] + even[9];
odd[7] = even[7] + even[4] + even[8];
odd[8] = even[8] + even[0] + even[5] +
even[7] + even[9];
odd[9] = even[9] + even[6] + even[8];
}
}
//Get count of all possible numbers of
//length "n" starting with digit 0, 1, 2, ..., 9
totalCount = 0;
if (useOdd == 1)
{
for (i = 0; i <= 9; i++)
totalCount += even[i];
}
else
{
for (i = 0; i <= 9; i++)
totalCount += odd[i];
}
return totalCount;
}
//Driver Code
public static void Main(String[] args)
{
char [, ]keypad = {{ '1' , '2' , '3' }, { '4' , '5' , '6' }, { '7' , '8' , '9' }, { '*' , '0' , '#' }};
Console.Write( "Count for numbers of length {0}: {1}\n" , 1, getCount(keypad, 1));
Console.Write( "Count for numbers of length {0}: {1}\n" , 2, getCount(keypad, 2));
Console.Write( "Count for numbers of length {0}: {1}\n" , 3, getCount(keypad, 3));
Console.Write( "Count for numbers of length {0}: {1}\n" , 4, getCount(keypad, 4));
Console.Write( "Count for numbers of length {0}: {1}\n" , 5, getCount(keypad, 5));
}
}
//This code is contributed by 29AjayKumar输出如下:
Count for numbers of length 1: 10
Count for numbers of length 2: 36
Count for numbers of length 3: 138
Count for numbers of length 4: 532
Count for numbers of length 5: 2062本文作者:阿努拉格·辛格(Anurag Singh)。如果发现任何不正确的地方, 或者想分享有关上述主题的更多信息, 请写评论。

![从字法上最小长度N的排列,使得对于正好为K个索引,a[i] a[i]+1](https://www.lsbin.com/wp-content/themes/begin%20lts/img/loading.png)