在数据挖掘和统计中, 层次聚类分析是一种聚类分析的方法, 其试图建立聚类的层次, 即基于层次的树型结构。
基本上, 有两种类型的层次聚类分析策略–
聚集聚类:
也称为自下而上的方法或分层的聚集聚类(HAC)。比扁平聚类返回的非结构化聚类集更具信息性的结构。该聚类算法不需要我们预先指定聚类的数量。自下而上的算法从一开始就将每个数据视为一个单例群集, 然后连续聚集成对的群集, 直到所有群集已合并为包含所有数据的单个群集。
算法:
given a dataset (d1, d2, d3, ....dN) of size N
# compute the distance matrix
for i=1 to N:
# as the distance matrix is symmetric about
# the primary diagonal so we compute only lower
# part of the primary diagonal
for j=1 to i:
dis_mat[i][j] = distance[di, dj]
each data point is a singleton cluster
repeat
merge the two cluster having minimum distance
update the distance matrix
untill only a single cluster remains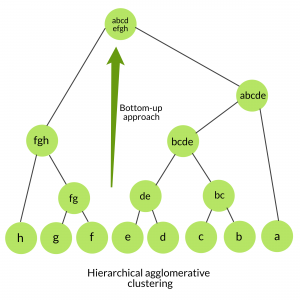
使用scikit-learn库的上述算法的Python实现:
from sklearn.cluster import AgglomerativeClustering
import numpy as np
# randomly chosen dataset
X = np.array([[ 1 , 2 ], [ 1 , 4 ], [ 1 , 0 ], [ 4 , 2 ], [ 4 , 4 ], [ 4 , 0 ]])
# here we need to mention the number of clusters
# otherwise the result will be a single cluster
# containing all the data
clustering = AgglomerativeClustering(n_clusters = 2 ).fit(X)
# print the class labels
print (clustering.labels_)输出:
[1, 1, 1, 0, 0, 0]分裂聚类:
也称为自顶向下方法。该算法也不需要预先指定簇的数量。自上而下的群集需要一种用于拆分包含整个数据的群集的方法, 然后通过递归方式拆分群集, 直到将单个数据拆分为单例群集为止。
算法:
given a dataset (d1, d2, d3, ....dN) of size N
at the top we have all data in one cluster
the cluster is split using a flat clustering method eg. K-Means etc
repeat
choose the best cluster among all the clusters to split
split that cluster by the flat clustering algorithm
untill each data is in its own singleton cluster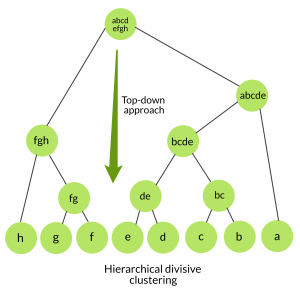
层次集聚vs分裂聚类–
- 分裂聚类更多复杂与聚集聚类相比, 在分散聚类的情况下, 我们需要一种扁平聚类方法作为"子例程"来拆分每个聚类, 直到每个数据具有其自己的单例聚类。
- 分裂聚类更多有效率的如果我们一直没有生成完整的层次结构, 直到单个数据离开。天真的聚集聚类的时间复杂度是上3)因为我们在N-1次迭代的每一次中都详尽扫描了N x N矩阵dist_mat以获得最低距离。使用优先级队列数据结构, 我们可以将复杂度降低为上2登录)。通过使用更多的优化, 可以归结为上2)。对于在给定固定数量的顶层的情况下进行分裂聚类而言, 使用有效的平坦算法(例如K-Means), 分裂算法在模式和簇的数量上是线性的。
- 除法算法也更多准确。聚集聚类通过考虑局部模式或邻近点来做出决策, 而无需首先考虑数据的全局分布。这些早期的决定不能撤消。而分裂式群集在做出顶级分区决策时会考虑数据的全局分布。
首先, 你的面试准备可通过以下方式增强你的数据结构概念:Python DS课程。

