ML：在Python中使用SMOTE和Near Miss算法处理不平衡数据

2021年5月2日16:20:24 发表评论 2,056 次浏览

本文概述

在机器学习和数据科学中, 我们经常遇到一个叫做数据分配不平衡, 通常发生在其中一类的观测值比其他类高或低得多的情况下。由于机器学习算法倾向于通过减少错误来提高准确性, 因此它们不考虑类的分布。此问题在以下示例中很普遍欺诈识别, 异常检测, 面部识别等等

决策树和Logistic回归等标准ML技术对多数阶级, 他们往往会忽略少数派。他们只倾向于预测多数派, 因此, 与多数派相比, 少数派的分类有重大错误。用更专业的话来说, 如果我们的数据集中的数据分布不平衡, 那么我们的模型就更容易出现少数群体的类别可忽略或更少的情况召回.

不平衡数据处理技术：主要有2种主要算法, 广泛用于处理不平衡的类分布。

  1. SMOTE
  2. Near Miss算法

SMOTE(少数民族综合采样技术)–过度采样

SMOTE(合成少数群体过采样技术)是解决不平衡问题的最常用过采样方法之一。

它的目的是通过随机复制少数族裔的例子来平衡阶级分布。

SMOTE在现有少数派实例之间综合了新的少数派实例。它产生

线性插值的虚拟训练记录

少数族裔。通过为少数群体类别中的每个示例随机选择一个或多个k最近邻来生成这些综合训练记录。经过过采样处理后, 将重建数据, 并且可以将几种分类模型应用于处理后的数据。

关于SMOTE算法如何工作的更多深刻见解！

第1步：

设定少数群体

一种

, 每个

$ x \ in A $

,

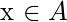
x的k个近邻

通过计算得到

欧氏距离

之间

X

以及集合中的所有其他样本

一种

.

第2步：

采样率

ñ

根据不平衡比例设置。对于每个

$ x \ in A $

,

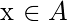
ñ

实例(即x1, x2, …xn)是从其k个最近邻居中随机选择的, 它们构成了集合

$ A_1 $

.

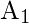
第三步：

对于每个示例

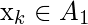
$ x_k \在A_1 $中

(k = 1, 2, 3…N), 以下公式用于生成新示例：

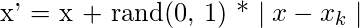
$ x'= x + rand（0，1）* \ mid x-x_k \ mid $

其中rand(0, 1)表示0到1之间的随机数。

NearMiss算法–欠采样

NearMiss是欠采样技术。它旨在通过随机消除多数班级例子来平衡班级分配。当两个不同类的实例彼此非常接近时, 我们将删除多数类的实例, 以增加两个类之间的空间。这有助于分类过程。

为了防止问题

信息丢失

在大多数欠采样技术中,

近邻

方法被广泛使用。

有关近邻方法工作的基本直觉如下：

步骤1：该方法首先找到多数类的所有实例与少数类的实例之间的距离。这里, 多数类别将被欠采样。

步骤2：然后, 选择与少数类中的实例具有最小距离的多数类的n个实例。

步骤3：如果少数类中有k个实例, 则最接近的方法将得出多数类中的k * n个实例。

为了在多数类中查找n个最接近的实例, 应用NearMiss算法有多种变体：

  1. NearMiss –版本1：它选择多数类的样本, 其平均距离为k最近的少数群体的实例最小。
  2. NearMiss –版本2：它选择多数类的样本, 其平均距离为k最远少数群体的实例最小。
  3. NearMiss –版本3：它分两个步骤工作。首先, 对于每个少数族裔实例, M个最近的邻居将被存储。然后最后, 选择多数类实例, 这些实例与N个最近邻居的平均距离最大。

本文有助于更好地理解和动手实践, 以了解如何在不同的不平衡数据处理技术之间进行最佳选择。

加载库和数据文件

数据集由信用卡进行的交易组成。该数据集具有

284, 807笔交易中的492笔欺诈交易

。这使其高度不平衡, 积极类别(欺诈)占所有交易的0.172％。

数据集可以从以下位置下载

这里

.

# import necessary modules 
import pandas  as pd
import matplotlib.pyplot as plt
import numpy as np
from sklearn.linear_model import LogisticRegression
from sklearn.preprocessing import StandardScaler
from sklearn.metrics import confusion_matrix, classification_report
  
# load the data set
data = pd.read_csv( 'creditcard.csv' )
  
# print info about columns in the dataframe
print (data.info())

输出如下：

RangeIndex: 284807 entries, 0 to 284806
Data columns (total 31 columns):
Time      284807 non-null float64
V1        284807 non-null float64
V2        284807 non-null float64
V3        284807 non-null float64
V4        284807 non-null float64
V5        284807 non-null float64
V6        284807 non-null float64
V7        284807 non-null float64
V8        284807 non-null float64
V9        284807 non-null float64
V10       284807 non-null float64
V11       284807 non-null float64
V12       284807 non-null float64
V13       284807 non-null float64
V14       284807 non-null float64
V15       284807 non-null float64
V16       284807 non-null float64
V17       284807 non-null float64
V18       284807 non-null float64
V19       284807 non-null float64
V20       284807 non-null float64
V21       284807 non-null float64
V22       284807 non-null float64
V23       284807 non-null float64
V24       284807 non-null float64
V25       284807 non-null float64
V26       284807 non-null float64
V27       284807 non-null float64
V28       284807 non-null float64
Amount    284807 non-null float64
Class     284807 non-null int64
# normalise the amount column
data[ 'normAmount' ] = StandardScaler().fit_transform(np.array(data[ 'Amount' ]).reshape( - 1 , 1 ))
  
# drop Time and Amount columns as they are not relevant for prediction purpose 
data = data.drop([ 'Time' , 'Amount' ], axis = 1 )
  
# as you can see there are 492 fraud transactions.
data[ 'Class' ].value_counts()

输出如下：

0    284315
       1       492

将数据分为测试集和训练集

from sklearn.model_selection import train_test_split
  
# split into 70:30 ration
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.3 , random_state = 0 )
  
# describes info about train and test set
print ( "Number transactions X_train dataset: " , X_train.shape)
print ( "Number transactions y_train dataset: " , y_train.shape)
print ( "Number transactions X_test dataset: " , X_test.shape)
print ( "Number transactions y_test dataset: " , y_test.shape)

输出如下：

Number transactions X_train dataset:  (199364, 29)
      Number transactions y_train dataset:  (199364, 1)
      Number transactions X_test dataset:  (85443, 29)
      Number transactions y_test dataset:  (85443, 1)

现在训练模型而不处理不平衡的班级分布

# logistic regression object
lr = LogisticRegression()
  
# train the model on train set
lr.fit(X_train, y_train.ravel())
  
predictions = lr.predict(X_test)
  
# print classification report
print (classification_report(y_test, predictions))

输出如下：

precision   recall   f1-score  support

           0       1.00      1.00      1.00     85296
           1       0.88      0.62      0.73       147

    accuracy                           1.00     85443
   macro avg       0.94      0.81      0.86     85443
weighted avg       1.00      1.00      1.00     85443

准确度为100％, 但是你是否注意到一些奇怪的东西？

少数民族阶层的召回很少。证明该模型更偏向多数派。因此, 证明这不是最佳模型。

现在, 我们将应用不同的

不平衡的数据处理技术

并查看其准确性和召回结果。

使用SMOTE算法

你可以从中检查所有参数这里.

print ( "Before OverSampling, counts of label '1': {}" . format ( sum (y_train = = 1 )))
print ( "Before OverSampling, counts of label '0': {} \n" . format ( sum (y_train = = 0 )))
  
# import SMOTE module from imblearn library
# pip install imblearn (if you don't have imblearn in your system)
from imblearn.over_sampling import SMOTE
sm = SMOTE(random_state = 2 )
X_train_res, y_train_res = sm.fit_sample(X_train, y_train.ravel())
  
print ( 'After OverSampling, the shape of train_X: {}' . format (X_train_res.shape))
print ( 'After OverSampling, the shape of train_y: {} \n' . format (y_train_res.shape))
  
print ( "After OverSampling, counts of label '1': {}" . format ( sum (y_train_res = = 1 )))
print ( "After OverSampling, counts of label '0': {}" . format ( sum (y_train_res = = 0 )))

输出如下：

Before OverSampling, counts of label '1': [345]
Before OverSampling, counts of label '0': [199019] 

After OverSampling, the shape of train_X: (398038, 29)
After OverSampling, the shape of train_y: (398038, ) 

After OverSampling, counts of label '1': 199019
After OverSampling, counts of label '0': 199019

看！

SMOTE算法对少数实例进行了过度采样, 使其等于多数类。两种类别的记录数量相等。更具体地说, 少数派已增加到多数派的总数。

现在, 在应用SMOTE算法(过采样)后, 可以看到准确性和召回率结果。

预测和召回

lr1 = LogisticRegression()
lr1.fit(X_train_res, y_train_res.ravel())
predictions = lr1.predict(X_test)
  
# print classification report
print (classification_report(y_test, predictions))

输出如下：

precision   recall   f1-score  support

           0       1.00      0.98      0.99     85296
           1       0.06      0.92      0.11       147

    accuracy                           0.98     85443
   macro avg       0.53      0.95      0.55     85443
weighted avg       1.00      0.98      0.99     85443

哇

, 与以前的模型相比, 我们的准确性降低到98％, 但少数族裔的召回值也提高了92％。与前一个模型相比, 这是一个很好的模型。回想起来很棒。

现在, 我们将应用NearMiss技术对多数类别进行欠采样, 以查看其准确性和召回结果。

NearMiss算法：

你可以从中检查所有参数这里.

print ( "Before Undersampling, counts of label '1': {}" . format ( sum (y_train = = 1 )))
print ( "Before Undersampling, counts of label '0': {} \n" . format ( sum (y_train = = 0 )))
  
# apply near miss
from imblearn.under_sampling import NearMiss
nr = NearMiss()
  
X_train_miss, y_train_miss = nr.fit_sample(X_train, y_train.ravel())
  
print ( 'After Undersampling, the shape of train_X: {}' . format (X_train_miss.shape))
print ( 'After Undersampling, the shape of train_y: {} \n' . format (y_train_miss.shape))
  
print ( "After Undersampling, counts of label '1': {}" . format ( sum (y_train_miss = = 1 )))
print ( "After Undersampling, counts of label '0': {}" . format ( sum (y_train_miss = = 0 )))

输出如下：

Before Undersampling, counts of label '1': [345]
Before Undersampling, counts of label '0': [199019] 

After Undersampling, the shape of train_X: (690, 29)
After Undersampling, the shape of train_y: (690, ) 

After Undersampling, counts of label '1': 345
After Undersampling, counts of label '0': 345

NearMiss算法对多数实例进行了欠采样, 使其等于多数类。在这里, 多数类已减少为少数类的总数, 因此两个类的记录数均相等。

预测和召回

# train the model on train set
lr2 = LogisticRegression()
lr2.fit(X_train_miss, y_train_miss.ravel())
predictions = lr2.predict(X_test)
  
# print classification report
print (classification_report(y_test, predictions))

输出如下：

precision    recall   f1-score   support

           0       1.00      0.56      0.72     85296
           1       0.00      0.95      0.01       147

    accuracy                           0.56     85443
   macro avg       0.50      0.75      0.36     85443
weighted avg       1.00      0.56      0.72     85443

该模型比第一个模型更好, 因为它可以更好地分类, 并且少数类别的召回价值为95％。但由于多数阶层的抽样不足, 其召回率已降至56％。因此, 在这种情况下, SMOTE为我提供了很高的准确性和召回率, 我将继续使用该模型！ 🙂

首先, 你的面试准备可通过以下方式增强你的数据结构概念：Python DS课程。

木子山

发表评论

:?: :razz: :sad: :evil: :!: :smile: :oops: :grin: :eek: :shock: :???: :cool: :lol: :mad: :twisted: :roll: :wink: :idea: :arrow: :neutral: :cry: :mrgreen: