ML模糊聚类详细介绍和指南

先决条件： 机器学习中的聚类

什么是聚类？

聚类是一种无监督的机器学习技术, 可根据给定数据彼此之间的距离(相似性)将其分为不同的簇。

无监督k均值聚类算法将位于某个特定聚类中的任何点的值设置为0或1, 即true或false。但是模糊逻辑给出了位于任一群集中的任何特定数据点的模糊值。在这里, 在模糊c均值聚类中, 我们找出数据点的质心, 然后计算每个数据点与给定质心的距离, 直到形成的聚类变得恒定为止。

假设给定的数据点是{(1, 3), (2, 5), (6, 8), (7, 9)}

执行算法的步骤是：

步骤1：将数据点随机初始化为所需数量的群集。

假设有两个要在其中划分数据的簇, 随机初始化数据点。每个数据点都位于两个群集中, 它们具有一些成员资格值, 在初始状态下可以假定任何成员资格值。

下表代表每个群集中数据点的值及其成员资格(gamma)。

Cluster    (1, 3)    (2, 5)    (4, 8)    (7, 9)
1)          0.8        0.7       0.2       0.1
2)          0.2        0.3       0.8       0.9

步骤2：找出质心。

找出质心(V)的公式为：

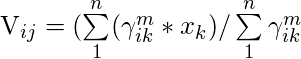
其中，µ为数据点的模糊隶属度值，m为模糊参数(一般取2)，xk为数据点。

这里,

V11  = (0.82 *1 + 0.72 * 2 + 0.22 * 4 + 0.12 * 7) /( (0.82 + 0.72  + 0.22  + 0.12 ) = 1.568
V12  = (0.82 *3 + 0.72 * 5 + 0.22 * 8 + 0.12 * 9) /( (0.82 + 0.72  + 0.22  + 0.12 ) = 4.051
V11  = (0.22 *1 + 0.32 * 2 + 0.82 * 4 + 0.92 * 7) /( (0.22 + 0.32  + 0.82  + 0.92 ) = 5.35
V11  = (0.22 *3 + 0.32 * 5 + 0.82 * 8 + 0.92 * 9) /( (0.22 + 0.32  + 0.82  + 0.92 ) = 8.215

Centroids are: (1.568, 4.051) and (5.35, 8.215)

步骤3：找出每个点到质心的距离。

D11 = ((1 - 1.568)^2 + (3 - 4.051)^2)^0.5 = 1.2
D12 = ((1 - 5.35)^2 + (3 - 8.215)^2)^0.5 = 6.79

同样, 所有其他点的距离都是从两个质心计算得出的。

步骤4：更新成员资格值。

第1点的新成员值是:

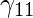
\gamma_{11} = [{ [(1.2)^2 / (1.2)^2] + [(1.2)^2 / (6.79)^2]} ^ {(1 / (2 – 1))} ]^-1 = 0.96

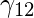
\gamma_{12} = [{ [(6.79)^2 / (6.79)^2] + [(6.79)^2 / (1.2)^2]} ^ {(1 / (2 – 1))} ]^-1 = 0.04

或者,

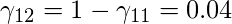
同样, 计算所有其他成员资格值, 并更新矩阵。

步骤5：重复步骤(2-4), 直到获得成员资格值的常数值或差值小于公差值(一个较小的值为止, 此值允许接受两次后续更新的值的差值)。

步骤6：

对获得的成员资格值进行模糊化处理。

实现：Fuzzy scikit学习库具有可用于Python的Fuzzy C均值的预定义函数。要使用模糊C均值, 你需要安装skfuzzy库。

pip install sklearn
pip install skfuzzy

---