特征缩放是一种在固定范围内标准化数据中存在的独立特征的技术。它是在数据预处理期间执行的。
加工:
给定具有以下特征的数据集-年龄, 工资, BHK公寓, 其数据大小为5000人, 每个人具有这些独立的数据特征。
每个数据点标记为:
- 1级-是(指具有给定年龄, 薪水和BHK公寓特征值的人可以购买该物业)
- 2类-否(具有给定年龄, 薪水和BHK公寓特征值的人无法购买该物业)。
通过使用数据集训练模型, 人们旨在建立一个模型, 该模型可以预测是否可以购买具有给定特征值的房产。
训练模型后, 可以创建带有给定数据集中的数据点的N维(其中N是数据集中存在的要素数量)图。下图是该模型的理想表示。
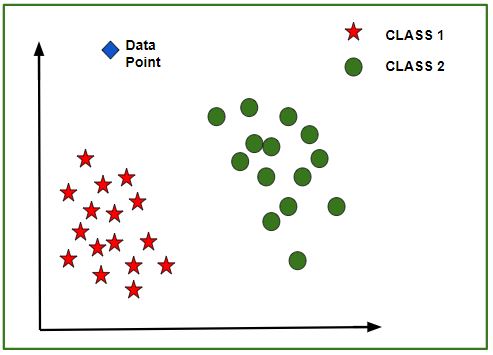
如图所示, 恒星数据点属于1类–是和圆圈代表2类–否标签, 然后使用这些数据点对模型进行训练。现在给出了一个新的数据点(如图所示的钻石), 并且对于上述3个要素(年龄, 工资, BHK公寓)具有不同的独立值。模型必须预测该数据点是属于是还是否。
新数据点类别的预测:
该模型从每个类组的质心计算此数据点的距离。最后, 该数据点将属于该类, 该类与该类之间将具有最小的质心距离。
可以使用以下方法计算质心和数据点之间的距离:
欧氏距离:
它是每个类的数据点和质心的坐标(特征值–年龄, 工资, BHK公寓)之间的差平方和的平方根。毕达哥拉斯定理给出该公式。
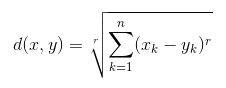
其中x是数据点值, y是质心值, k是no。特征值的示例, 例如:给定数据集的k = 3
曼哈顿距离:
它被计算为每个类的数据点和质心之间的坐标(特征值)的绝对差之和。
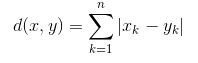
Minkowski Distance:这是上述两种方法的概括。如图所示, 可以使用不同的值来找到r。
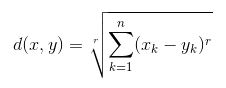
特征缩放需求:
给定的数据集包含3个特征-年龄, 工资, BHK公寓。考虑年龄范围为10-60, 工资为1 Lac-40 Lacs, BHK为1-5。所有这些特征彼此独立。
假设类别1的质心为[40, 22 Lacs, 3], 要预测的数据点为[57, 33 Lacs, 2]。
使用曼哈顿方法,
Distance = (|(40 - 57)| + |(2200000 - 3300000)| + |(3 - 2)|)可以看出, 在预测给定数据点的类别时, 薪水特征将主导所有其他特征, 并且由于所有特征彼此独立, 即一个人的薪水与他/她的年龄或与他/她持平的要求无关。她有。这意味着模型将始终预测错误。
因此, 解决此问题的简单方法是特征缩放。特征缩放算法将在固定范围内(例如[-1、1]或[0、1])缩放年龄, 工资, BHK。然后, 没有任何特征可以主导其他特征。

