ML Logistic回归中的成本函数

对于线性回归, 成本函数为–

但是对于Logistic回归,

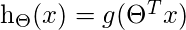
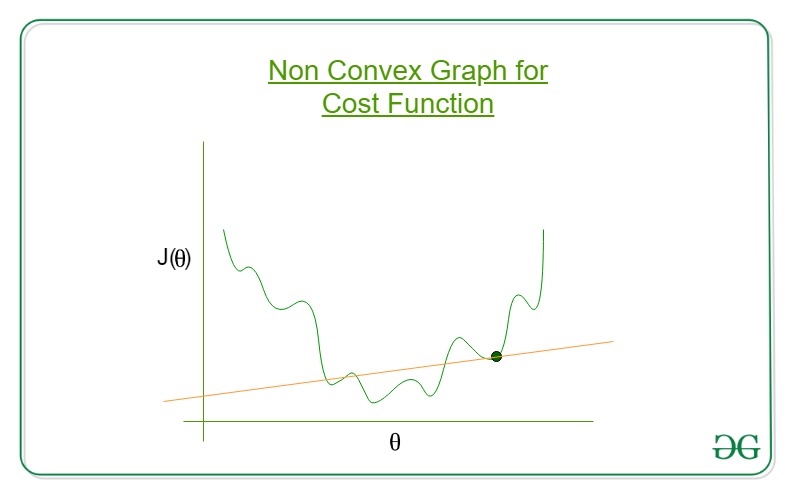
这将导致非凸成本函数。但这会导致成本函数具有局部最优值, 这对于梯度下降计算全局最优值来说是一个很大的问题。

因此, 对于Logistic回归, 成本函数为

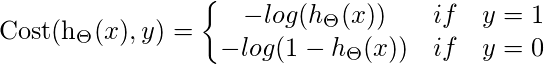
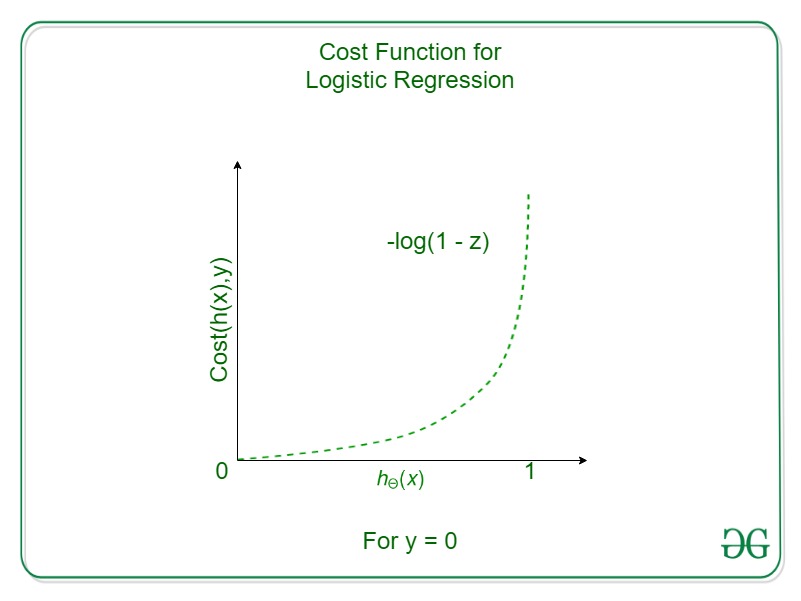
如果y = 1

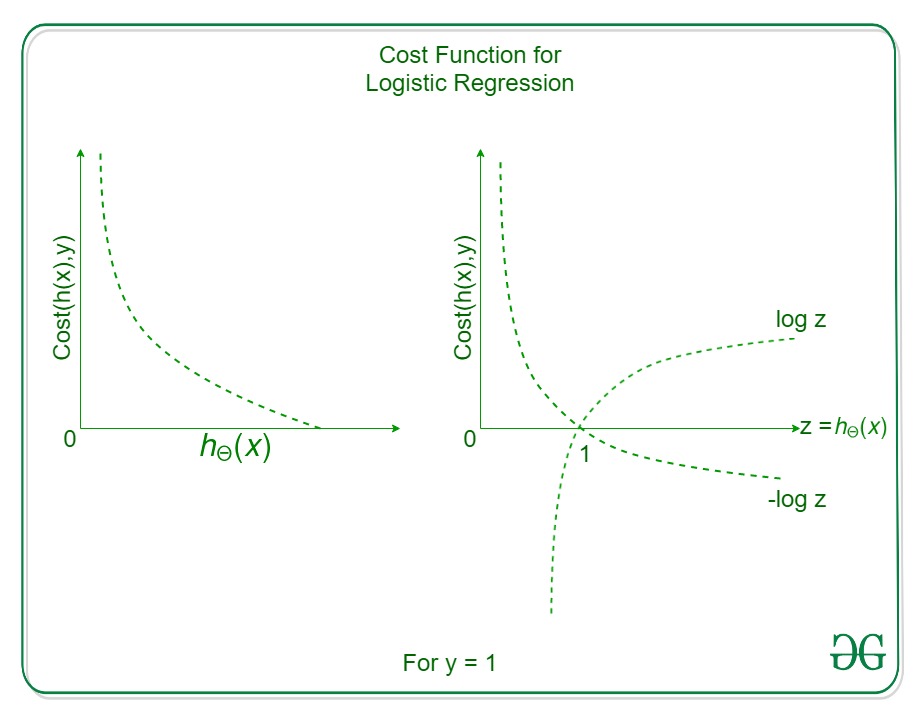
Cost = 0 if y = 1, hθ(x) = 1

但是

hθ(x) -> 0

Cost -> Infinity

所以,

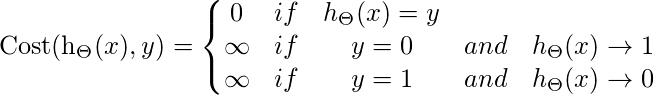
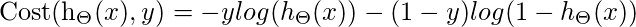
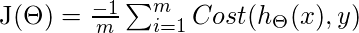
拟合参数θ, 必须将J(θ)最小化, 并且为此需要梯度下降。

梯度下降 -看起来与线性回归相似, 但区别在于假设hθ(X)

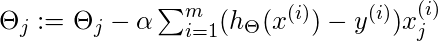
首先, 你的面试准备可通过以下方式增强你的数据结构概念：Python DS课程。

---