算法设计：迭代后序遍历|S2（使用栈stack）

本文概述

• C
• Java
• python

我们已经讨论了一个简单的使用两个堆栈进行迭代后遍历在上一篇文章中。在这篇文章中, 讨论了只有一个堆栈的方法。

这个想法是使用左指针向下移动到最左边的节点。向下移动时, 推动根和根的右子堆叠。到达最左边的节点后, 如果没有正确的子节点, 则将其打印出来。如果它有合适的孩子, 则更改根目录, 以便在处理合适的孩子之前进行处理。

以下是详细的算法。

1.1 Create an empty stack
2.1 Do following while root is not NULL
    a) Push root's right child and then root to stack.
    b) Set root as root's left child.
2.2 Pop an item from stack and set it as root.
    a) If the popped item has a right child and the right child 
       is at top of stack, then remove the right child from stack, push the root back and set root as root's right child.
    b) Else print root's data and set root as NULL.
2.3 Repeat steps 2.1 and 2.2 while stack is not empty.

让我们考虑下面的树

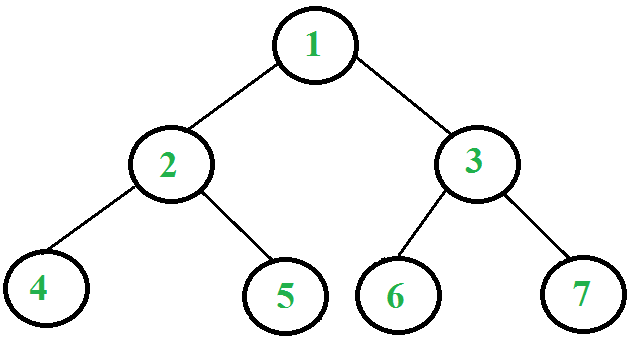
以下是使用一个堆栈打印上述树的事后遍历的步骤。

1. Right child of 1 exists. 
   Push 3 to stack. Push 1 to stack. Move to left child.
        Stack: 3, 1

2. Right child of 2 exists. 
   Push 5 to stack. Push 2 to stack. Move to left child.
        Stack: 3, 1, 5, 2

3. Right child of 4 doesn't exist. '
   Push 4 to stack. Move to left child.
        Stack: 3, 1, 5, 2, 4

4. Current node is NULL. 
   Pop 4 from stack. Right child of 4 doesn't exist. 
   Print 4. Set current node to NULL.
        Stack: 3, 1, 5, 2

5. Current node is NULL. 
    Pop 2 from stack. Since right child of 2 equals stack top element, pop 5 from stack. Now push 2 to stack.     
    Move current node to right child of 2 i.e. 5
        Stack: 3, 1, 2

6. Right child of 5 doesn't exist. Push 5 to stack. Move to left child.
        Stack: 3, 1, 2, 5

7. Current node is NULL. Pop 5 from stack. Right child of 5 doesn't exist. 
   Print 5. Set current node to NULL.
        Stack: 3, 1, 2

8. Current node is NULL. Pop 2 from stack. 
   Right child of 2 is not equal to stack top element. 
   Print 2. Set current node to NULL.
        Stack: 3, 1

9. Current node is NULL. Pop 1 from stack. 
   Since right child of 1 equals stack top element, pop 3 from stack. 
   Now push 1 to stack. Move current node to right child of 1 i.e. 3
        Stack: 1

10. Repeat the same as above steps and Print 6, 7 and 3. 
    Pop 1 and Print 1.

C

//C program for iterative postorder traversal using one stack
#include <stdio.h>
#include <stdlib.h>
  
//Maximum stack size
#define MAX_SIZE 100
  
//A tree node
struct Node
{
     int data;
     struct Node *left, *right;
};
  
//Stack type
struct Stack
{
     int size;
     int top;
     struct Node* *array;
};
  
//A utility function to create a new tree node
struct Node* newNode( int data)
{
     struct Node* node = ( struct Node*) malloc ( sizeof ( struct Node));
     node->data = data;
     node->left = node->right = NULL;
     return node;
}
  
//A utility function to create a stack of given size
struct Stack* createStack( int size)
{
     struct Stack* stack = ( struct Stack*) malloc ( sizeof ( struct Stack));
     stack->size = size;
     stack->top = -1;
     stack->array = ( struct Node**) malloc (stack->size * sizeof ( struct Node*));
     return stack;
}
  
//BASIC OPERATIONS OF STACK
int isFull( struct Stack* stack)
{  return stack->top - 1 == stack->size; }
  
int isEmpty( struct Stack* stack)
{  return stack->top == -1; }
  
void push( struct Stack* stack, struct Node* node)
{
     if (isFull(stack))
         return ;
     stack->array[++stack->top] = node;
}
  
struct Node* pop( struct Stack* stack)
{
     if (isEmpty(stack))
         return NULL;
     return stack->array[stack->top--];
}
  
struct Node* peek( struct Stack* stack)
{
     if (isEmpty(stack))
         return NULL;
     return stack->array[stack->top];
}
  
//An iterative function to do postorder traversal of a given binary tree
void postOrderIterative( struct Node* root)
{
     //Check for empty tree
     if (root == NULL)
         return ;
      
     struct Stack* stack = createStack(MAX_SIZE);
     do
     {
         //Move to leftmost node
         while (root)
         {
             //Push root's right child and then root to stack.
             if (root->right)
                 push(stack, root->right);
             push(stack, root);
  
             //Set root as root's left child  
             root = root->left;
         }
  
         //Pop an item from stack and set it as root    
         root = pop(stack);
  
         //If the popped item has a right child and the right child is not
         //processed yet, then make sure right child is processed before root
         if (root->right && peek(stack) == root->right)
         {
             pop(stack);  //remove right child from stack
             push(stack, root);  //push root back to stack
             root = root->right; //change root so that the right 
                                 //child is processed next
         }
         else  //Else print root's data and set root as NULL
         {
             printf ( "%d " , root->data);
             root = NULL;
         }
     } while (!isEmpty(stack));
}
  
//Driver program to test above functions
int main()
{
     //Let us construct the tree shown in above figure
     struct Node* root = NULL;
     root = newNode(1);
     root->left = newNode(2);
     root->right = newNode(3);
     root->left->left = newNode(4);
     root->left->right = newNode(5);
     root->right->left = newNode(6);
     root->right->right = newNode(7);
     printf ( "Post order traversal of binary tree is :\n" );
     printf ( "[" );
     postOrderIterative(root);
     printf ( "]" );
      
  
     return 0;
}

Java

//A java program for iterative postorder traversal using stack
  
import java.util.ArrayList;
import java.util.Stack;
   
//A binary tree node
class Node 
{
     int data;
     Node left, right;
   
     Node( int item) 
     {
         data = item;
         left = right;
     }
}
   
class BinaryTree 
{
     Node root;
     ArrayList<Integer> list = new ArrayList<Integer>();
   
     //An iterative function to do postorder traversal 
     //of a given binary tree
     ArrayList<Integer> postOrderIterative(Node node) 
     {
         Stack<Node> S = new Stack<Node>();
           
         //Check for empty tree
         if (node == null )
             return list;
         S.push(node);
         Node prev = null ;
         while (!S.isEmpty()) 
         {
             Node current = S.peek();
   
             /* go down the tree in search of a leaf an if so process it 
             and pop stack otherwise move down */
             if (prev == null || prev.left == current || 
                                         prev.right == current) 
             {
                 if (current.left != null )
                     S.push(current.left);
                 else if (current.right != null )
                     S.push(current.right);
                 else
                 {
                     S.pop();
                     list.add(current.data);
                 }
   
                 /* go up the tree from left node, if the child is right 
                    push it onto stack otherwise process parent and pop 
                    stack */
             } 
             else if (current.left == prev) 
             {
                 if (current.right != null )
                     S.push(current.right);
                 else 
                 {
                     S.pop();
                     list.add(current.data);
                 }
                   
                 /* go up the tree from right node and after coming back
                  from right node process parent and pop stack */
             } 
             else if (current.right == prev) 
             {
                 S.pop();
                 list.add(current.data);
             }
   
             prev = current;
         }
   
         return list;
     }
   
     //Driver program to test above functions
     public static void main(String args[]) 
     {
      BinaryTree tree = new BinaryTree();
   
         //Let us create trees shown in above diagram
         tree.root = new Node( 1 );
         tree.root.left = new Node( 2 );
         tree.root.right = new Node( 3 );
         tree.root.left.left = new Node( 4 );
         tree.root.left.right = new Node( 5 );
         tree.root.right.left = new Node( 6 );
         tree.root.right.right = new Node( 7 );
   
         ArrayList<Integer> mylist = tree.postOrderIterative(tree.root);
           
         System.out.println( "Post order traversal of binary tree is :" );
         System.out.println(mylist);
     }
}
   
//This code has been contributed by Mayank Jaiswal

python

# Python program for iterative postorder traversal
# using one stack
  
# Stores the answer
ans = []
  
# A Binary tree node
class Node:
      
     # Constructor to create a new node
     def __init__( self , data):
         self .data = data
         self .left = None
         self .right = None
  
def peek(stack):
     if len (stack)> 0 :
         return stack[ - 1 ]
     return None
# A iterative function to do postorder traversal of 
# a given binary tree
def postOrderIterative(root):
          
     # Check for empty tree
     if root is None :
         return 
  
     stack = []
      
     while ( True ):
          
         while (root):
              # Push root's right child and then root to stack
              if root.right is not None :
                 stack.append(root.right)
              stack.append(root)
  
              # Set root as root's left child
              root = root.left
          
         # Pop an item from stack and set it as root
         root = stack.pop()
  
         # If the popped item has a right child and the
         # right child is not processed yet, then make sure
         # right child is processed before root
         if (root.right is not None and 
             peek(stack) = = root.right):
             stack.pop() # Remove right child from stack 
             stack.append(root) # Push root back to stack
             root = root.right # change root so that the 
                              # righ childis processed next
  
         # Else print root's data and set root as None
         else :
             ans.append(root.data) 
             root = None
  
         if ( len (stack) <= 0 ):
                 break
  
# Driver pogram to test above function
root = Node( 1 )
root.left = Node( 2 )
root.right = Node( 3 )
root.left.left = Node( 4 )
root.left.right = Node( 5 )
root.right.left = Node( 6 )
root.right.right = Node( 7 )
  
print "Post Order traversal of binary tree is"
postOrderIterative(root)
print ans
  
# This code is contributed by Nikhil Kumar Singh(nickzuck_007)

输出如下：

Post Order traversal of binary tree is
[4, 5, 2, 6, 7, 3, 1]

方法2：

向左移动两次, 同时直接推根节点两次。弹出时, 如果发现stack top()与root相同, 则转到root-> right, 否则打印root。

//Simple Java program to print PostOrder Traversal(Iterative)
import java.util.Stack;
  
//A binary tree node
class Node 
{
     int data;
     Node left, right;
  
     Node( int item) 
     {
         data = item;
         left = right;
     }
}
  
//create a postorder class
class PostOrder
{ 
     Node root;
      
     //An iterative function to do postorder traversal 
     //of a given binary tree
     private void postOrderIterative(Node root) {
         Stack<Node> stack = new Stack<>();
         while ( true ) {
             while (root != null ) {
                 stack.push(root);
                 stack.push(root);
                 root = root.left;
             }
              
             //Check for empty stack
             if (stack.empty()) return ;
             root = stack.pop();
              
             if (!stack.empty() && stack.peek() == root) root = root.right;
              
             else {
                  
                 System.out.print(root.data + " " ); root = null ;
             }
         }
     }
      
     //Driver program to test above functions
     public static void main(String args[]) 
     {
     PostOrder tree = new PostOrder();
          
         //Let us create trees shown in above diagram
         tree.root = new Node( 1 );
         tree.root.left = new Node( 2 );
         tree.root.right = new Node( 3 );
         tree.root.left.left = new Node( 4 );
         tree.root.left.right = new Node( 5 );
         tree.root.right.left = new Node( 6 );
         tree.root.right.right = new Node( 7 );
         System.out.println( "Post order traversal of binary tree is :" );
         tree.postOrderIterative(tree.root);
     }
}

输出如下：

Post Order traversal of binary tree is:
4, 5, 2, 6, 7, 3, 1

本文作者：阿什什·巴恩沃尔(Aashish Barnwal)。如果发现任何不正确的地方, 或者想分享有关上述主题的更多信息, 请发表评论。