难题：将一个正方形划分为N个较小的正方形

难题：查找的所有值ñ可以将一个正方形分解成N个较小的正方形, 并概述了进行这种解剖的算法。

解：要观察的基本点是一个具有4个直角的正方形。因此, 将其分成较小的正方形直角必须落入另一个正方形, 因为一个直角在一起将产生一个非正方形的数字。

现在, 考虑以下情况：

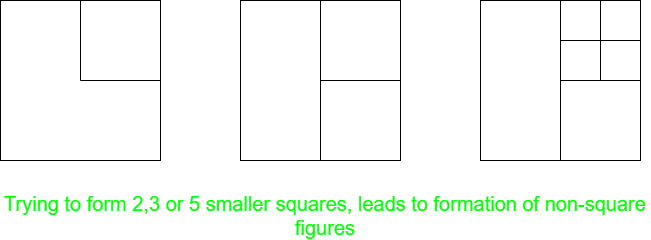
当N = 2、3或5时：不可能进行这种划分, 因为它违反了上述给定条件, 因此获得了不整形的图形。

当N = 4时：这是最简单的情况。只是从中心水平和垂直划分正方形。结果数字将有4个正方形。

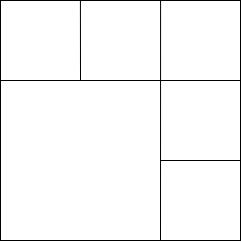
当N是偶数且大于4时:这种情况可以推广为考虑N = 2k，并沿给定的正方形的邻边形成2k - 1等的正方形。然而，每个小正方形的边长应该等于给定正方形长度的1/k。

例如:考虑如图所示的N = 6的例子，在这里我们沿着顶部和右侧形成了5个正方形，每个正方形的边(1/3)rd。另外，左边是边(2/k)的平方，总共是6个平方。

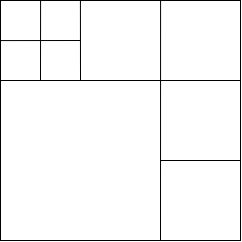
情况N是奇数且大于5:这种情况建立在N的偶数值的解之上。如果N是奇数，我们可以把它打破为N = 2k + 1，进一步可以写成N = 2(k - 1) + 3。现在，我们可以首先用上面的方法形成2(k - 1)个正方形，然后将得到的正方形除以4个更小的正方形，这将使总的正方形数增加3。

例如：考虑以下示例N = 9如图所示。在这里, 我们首先形成6平方, 然后将左上角的正方形分为4较小的正方形, 以获得总计9方块。

---