算法题：求最长连续子序列

2021年4月21日18:47:53 发表评论 731 次浏览

本文概述

给定整数数组, 请找到最长子序列的长度, 以使子序列中的元素为连续整数, 连续数字可以为任意顺序。

例子:

Input: arr[] = {1, 9, 3, 10, 4, 20, 2}
Output: 4
Explanation: 
The subsequence 1, 3, 4, 2 is the longest 
subsequence of consecutive elements

Input: arr[] = {36, 41, 56, 35, 44, 33, 34, 92, 43, 32, 42}
Output: 5
Explanation: 
The subsequence 36, 35, 33, 34, 32 is the longest 
subsequence of consecutive elements.

简单的方法：

这个想法是首先对数组进行排序, 然后找到具有连续元素的最长子数组。

对数组进行排序后, 运行循环并保持计数和最大值(均初始为零)。从头到尾运行一个循环, 如果当前元素不等于前一个元素(元素+1), 则将计数设置为1, 否则增加计数。用最大计数和最大更新最大值。

C++ 14

//C++ program to find longest
//contiguous subsequence
#include <bits/stdc++.h>
using namespace std;
 
//Returns length of the longest
//contiguous subsequence
int findLongestConseqSubseq( int arr[], int n)
{
     int ans = 0, count = 0;
 
     //sort the array
     sort(arr, arr + n);
 
     //find the maximum length
     //by traversing the array
     for ( int i = 0; i <n; i++) {
         //if the current element is equal
         //to previous element +1
         if (i> 0 && arr[i] == arr[i - 1] + 1)
             count++;
         //reset the count
         else
             count = 1;
 
         //update the maximum
         ans = max(ans, count);
     }
     return ans;
}
 
//Driver program
int main()
{
     int arr[] = { 1, 9, 3, 10, 4, 20, 2 };
     int n = sizeof arr /sizeof arr[0];
     cout <<"Length of the Longest contiguous subsequence is "
          <<findLongestConseqSubseq(arr, n);
     return 0;
}

Java

//Java program to find longest
//contiguous subsequence
import java.io.*;
import java.util.*;
 
class GFG{
     
static int findLongestConseqSubseq( int arr[], int n)
{
     
     //Sort the array
      Arrays.sort(arr);
      
       int ans = 0 , count = 1 ;
       
     //find the maximum length
     //by traversing the array
       for ( int i = 1 ; i <n; i++)
     {
         
         //If the current element is
         //equal to previous element +1
         if (arr[i] == arr[i - 1 ] + 1 )
             count++;
         else
             count = 1 ;
             
         //Update the maximum
         ans = Math.max(ans, count);
     }
     return ans;
}
 
//Driver code
public static void main (String[] args)
{
     int arr[] = { 1 , 9 , 3 , 10 , 4 , 20 , 2 };
       int n = arr.length;
       
       System.out.println( "Length of the Longest " +
                          "contiguous subsequence is " +
                          findLongestConseqSubseq(arr, n));
}
}
 
//This code is contributed by parascoding

输出如下：

Length of the Longest contiguous subsequence is 4

复杂度分析：

  • 时间复杂度：O(nLogn)。
    对数组进行排序的时间为O(nlogn)。
  • 辅助空间：O(1)。
    由于不需要额外的空间。

感谢Hao.W建议上述解决方案。

高效的解决方案：

这个问题可以在O(n)时间内使用高效的解决方案。这个想法是使用散列。我们首先将所有元素插入组。然后检查连续子序列的所有可能开始。

算法：

  1. 创建一个空哈希。
  2. 将所有数组元素插入哈希。
  3. 对每个元素arr [i]执行以下操作
  4. 检查此元素是否是子序列的起点。要检查这一点, 只需在哈希中查找arr [i] – 1(如果未找到), 则这是子序列的第一个元素。
  5. 如果此元素是第一个元素, 则从该元素开始计算连续的元素数。从arr [i] + 1进行迭代, 直到找到最后一个元素。
  6. 如果计数大于以前找到的最长子序列, 则更新它。

下图是上述方法的模拟：

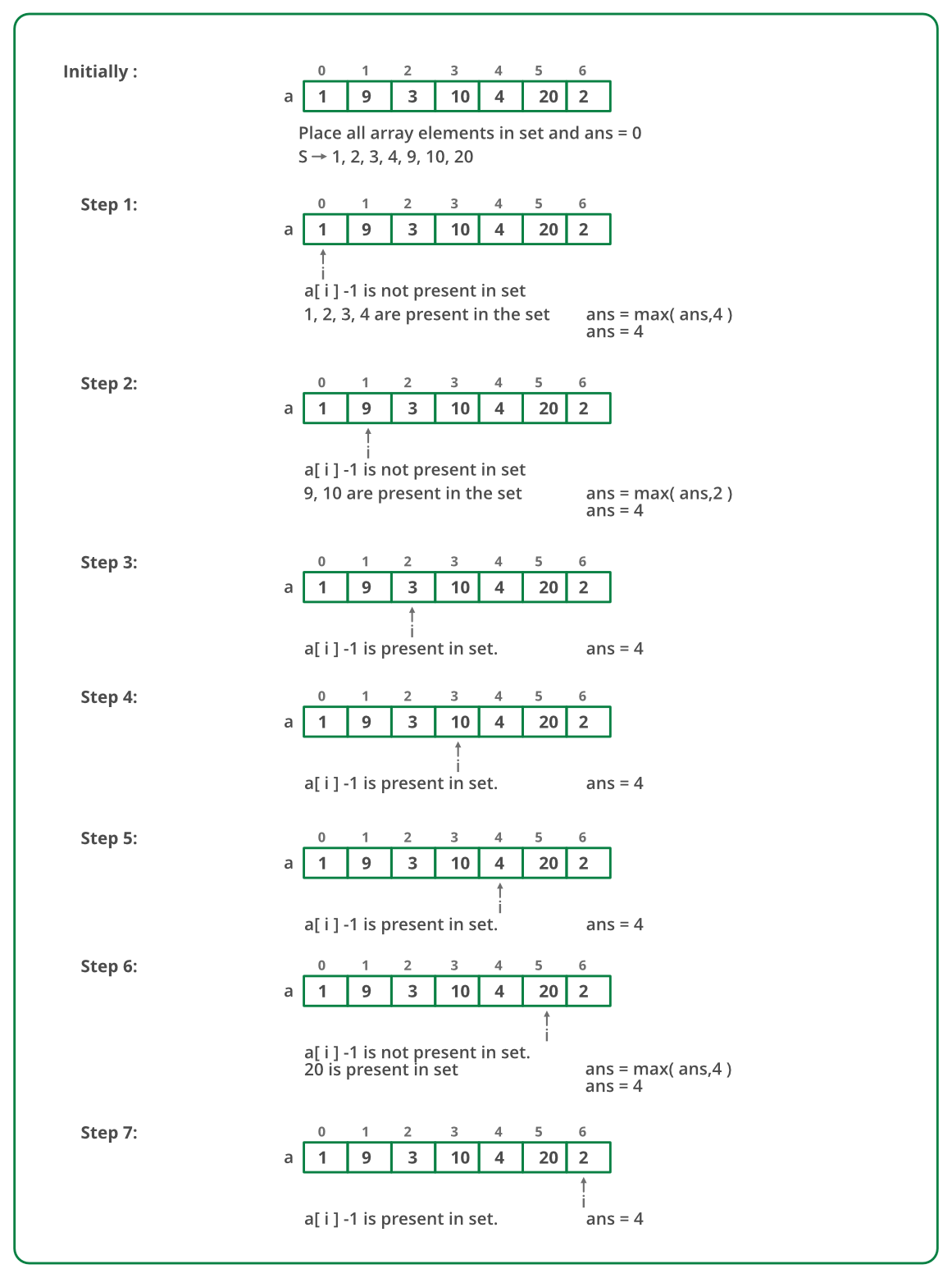
最长连续子序列1

下面是上述方法的实现：

C++

//C++ program to find longest
//contiguous subsequence
#include <bits/stdc++.h>
using namespace std;
 
//Returns length of the longest
//contiguous subsequence
int findLongestConseqSubseq( int arr[], int n)
{
     unordered_set<int> S;
     int ans = 0;
 
     //Hash all the array elements
     for ( int i = 0; i <n; i++)
         S.insert(arr[i]);
 
     //check each possible sequence from
     //the start then update optimal length
     for ( int i = 0; i <n; i++) {
         //if current element is the starting
         //element of a sequence
         if (S.find(arr[i] - 1) == S.end()) {
             //Then check for next elements
             //in the sequence
             int j = arr[i];
             while (S.find(j) != S.end())
                 j++;
 
             //update  optimal length if
             //this length is more
             ans = max(ans, j - arr[i]);
         }
     }
     return ans;
}
 
//Driver program
int main()
{
     int arr[] = { 1, 9, 3, 10, 4, 20, 2 };
     int n = sizeof arr /sizeof arr[0];
     cout <<"Length of the Longest contiguous subsequence is "
          <<findLongestConseqSubseq(arr, n);
     return 0;
}

Java

//Java program to find longest
//consecutive subsequence
import java.io.*;
import java.util.*;
 
class ArrayElements {
     //Returns length of the longest
     //consecutive subsequence
     static int findLongestConseqSubseq( int arr[], int n)
     {
         HashSet<Integer> S = new HashSet<Integer>();
         int ans = 0 ;
 
         //Hash all the array elements
         for ( int i = 0 ; i <n; ++i)
             S.add(arr[i]);
 
         //check each possible sequence from the start
         //then update optimal length
         for ( int i = 0 ; i <n; ++i) {
             //if current element is the starting
             //element of a sequence
             if (!S.contains(arr[i] - 1 )) {
                 //Then check for next elements
                 //in the sequence
                 int j = arr[i];
                 while (S.contains(j))
                     j++;
 
                 //update  optimal length if this
                 //length is more
                 if (ans <j - arr[i])
                     ans = j - arr[i];
             }
         }
         return ans;
     }
 
     //Testing program
     public static void main(String args[])
     {
         int arr[] = { 1 , 9 , 3 , 10 , 4 , 20 , 2 };
         int n = arr.length;
         System.out.println(
             "Length of the Longest consecutive subsequence is "
             + findLongestConseqSubseq(arr, n));
     }
}
//This code is contributed by Aakash Hasija

python

# Python program to find longest contiguous subsequence
 
from sets import Set
def findLongestConseqSubseq(arr, n):
 
     s = Set ()
     ans = 0
 
     # Hash all the array elements
     for ele in arr:
         s.add(ele)
 
     # check each possible sequence from the start
     # then update optimal length
     for i in range (n):
 
          # if current element is the starting
         # element of a sequence
         if (arr[i] - 1 ) not in s:
 
             # Then check for next elements in the
             # sequence
             j = arr[i]
             while (j in s):
                 j + = 1
 
             # update  optimal length if this length
             # is more
             ans = max (ans, j - arr[i])
     return ans
 
# Driver function
if __name__ = = '__main__' :
     n = 7
     arr = [ 1 , 9 , 3 , 10 , 4 , 20 , 2 ]
     print "Length of the Longest contiguous subsequence is " , print  findLongestConseqSubseq(arr, n)
         
# Contributed by: Harshit Sidhwa

C#

using System;
using System.Collections.Generic;
 
//C# program to find longest consecutive subsequence
 
public class ArrayElements {
     //Returns length of the longest consecutive subsequence
     public static int findLongestConseqSubseq( int [] arr, int n)
     {
         HashSet<int> S = new HashSet<int>();
         int ans = 0;
 
         //Hash all the array elements
         for ( int i = 0; i <n; ++i) {
             S.Add(arr[i]);
         }
 
         //check each possible sequence from the start
         //then update optimal length
         for ( int i = 0; i <n; ++i) {
             //if current element is the starting
             //element of a sequence
             if (!S.Contains(arr[i] - 1)) {
                 //Then check for next elements in the
                 //sequence
                 int j = arr[i];
                 while (S.Contains(j)) {
                     j++;
                 }
 
                 //update  optimal length if this length
                 //is more
                 if (ans <j - arr[i]) {
                     ans = j - arr[i];
                 }
             }
         }
         return ans;
     }
 
     //Testing program
     public static void Main( string [] args)
     {
         int [] arr = new int [] { 1, 9, 3, 10, 4, 20, 2 };
         int n = arr.Length;
         Console.WriteLine( "Length of the Longest consecutive subsequence is " + findLongestConseqSubseq(arr, n));
     }
}
 
//This code is contributed by Shrikant13

输出如下：

Length of the Longest contiguous subsequence is 4

复杂度分析：

  • 时间复杂度：O(n)。
    在散列插入和搜索花费O(1)时间的假设下, 只需要一个遍历, 时间复杂度为O(n)。
  • 辅助空间：O(n)。
    要将每个元素存储在哈希图中, 需要O(n)空间。

如果发现任何不正确的地方, 或者想分享有关上述主题的更多信息, 请写评论。

木子山

发表评论

:?: :razz: :sad: :evil: :!: :smile: :oops: :grin: :eek: :shock: :???: :cool: :lol: :mad: :twisted: :roll: :wink: :idea: :arrow: :neutral: :cry: :mrgreen: