回归分析指南：了解逻辑回归

先决条件：线性回归

本文讨论了Logistic回归的基础知识及其在Python中的实现。 Logistic回归基本上是一种监督分类算法。在分类问题中, 目标变量(或输出)y对于给定的一组特征(或输入)X只能采用离散值。

与普遍的看法相反, 逻辑回归是一种回归模型。该模型构建回归模型, 以预测给定数据条目属于编号为" 1"的类别的概率。就像线性回归假设数据遵循线性函数一样, 逻辑回归使用S型函数对数据进行建模。

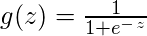
仅当将决策阈值引入画面时, 逻辑回归才成为分类技术。阈值的设置是Logistic回归的一个非常重要的方面, 并且取决于分类问题本身。

阈值的决定主要受以下因素的影响：精度和召回率。理想情况下, 我们希望精度和查全率都为1, 但这很少是这种情况。如果需要进行精确召回权衡, 我们使用以下参数来决定阈值：

1.低精度/高召回率：在我们希望减少误报的数量而不必减少误报的数量的应用中, 我们选择的决策值应具有较低的Precision值或较高的Recall值。例如, 在癌症诊断应用程序中, 我们不希望任何被误诊为癌症的患者都被分类为未受影响。这是因为, 可以通过进一步的医学疾病检测到癌症的缺乏, 但是在已经被拒绝的候选人中不能检测到疾病的存在。

2.高精度/低召回率：在我们想要减少误报的数量而不必减少误报的数量的应用中, 我们选择一个具有高Precision值或低Recall值的决策值。例如, 如果我们要分类客户对个性化广告的正面还是负面反应, 则我们要绝对确定客户会对广告正面反应, 因为否则, 负面反应可能会导致潜在的销售损失。

根据类别数, Logistic回归可分为：

1. 二项式：目标变量只能有2种可能的类型：" 0"或" 1", 分别表示"获胜"与"失败", "通过"与"失败", "无效"与"有效"等。
2. 多项式：目标变量可以具有3种或多种不排序的可能类型(即类型没有定量意义), 例如"疾病A"与"疾病B"与"疾病C"。
3. 顺序：它处理具有排序类别的目标变量。例如, 测试分数可以归类为："非常差", "差", "好", "非常好"。在这里, 可以给每个类别一个分数, 例如0、1、2、3。

首先, 我们探讨Logistic回归的最简单形式, 即二项式Logistic回归.

二项式Logistic回归

考虑一个示例数据集, 该数据集将学习时间与考试结果对应起来。结果只能采用两个值, 即passed(1)或failed(0)：

Hours(x) 

     0.50 

     0.75 

     1.00 

     1.25 

     1.50 

     1.75 

     2.00 

     2.25 

     2.50 

     2.75 

     3.00 

     3.25 

     3.50 

     3.75 

     4.00 

     4.25 

     4.50 

     4.75 

     5.00 

     5.50 

    

    

     Pass(y) 

     0 

     0 

     0 

     0 

     0 

     0 

     1 

     0 

     1 

     0 

     1 

     0 

     1 

     0 

     1 

     1 

     1 

     1 

     1 

     1

所以, 我们有

即y是分类目标变量, 只能采用两种可能的类型：" 0"或" 1"。

为了概括我们的模型, 我们假设：

数据集具有" p"个特征变量和" n"个观测值。

特征矩阵表示为：

这里,

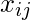
表示的值

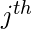
功能

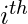
观察。

在这里, 我们保持租赁的惯例

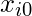
=1。(请继续阅读, 稍后你将了解逻辑)。

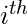
观察,

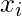
, 可以表示为：

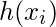
代表的预期响应

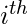
观察, 即

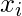
。我们用来计算的公式

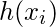
叫做

假设

.

如果你已经进行了线性回归, 你应该记得在线性回归中, 我们用于预测的假设是：

其中

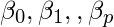
是回归系数。

让回归系数矩阵/向量

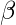
是：

然后, 以更紧凑的形式

现在取1的原因非常清楚。我们需要做一个矩阵乘积, 但是在原始假设公式中并没有实际相乘的结果。因此, 我们定义= 1。

现在, 如果我们尝试对上述问题应用线性回归, 则可能会使用上面讨论的假设获得连续值。而且, 对于

取大于1或小于0的值。

因此, 对分类假设进行了一些修改：

其中

叫做

物流功能

或者

乙状结肠功能

.

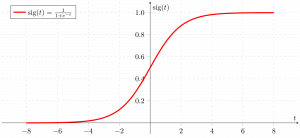
这是显示g(z)的图：

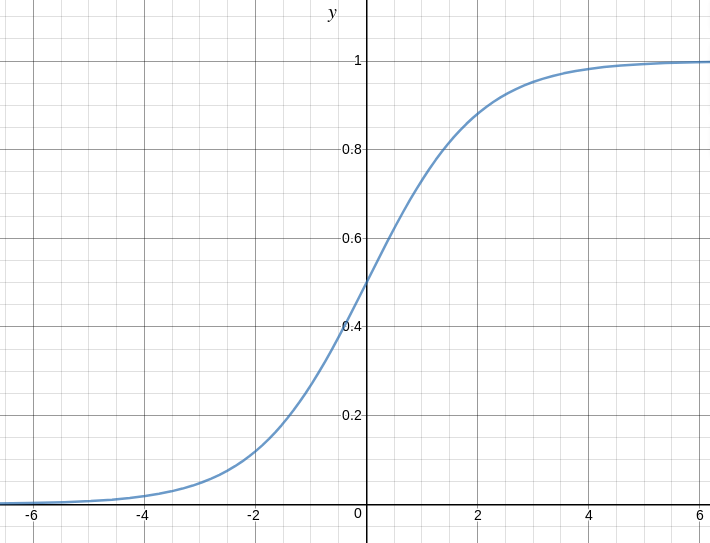
我们可以从上图推断：

g(z)趋于1

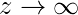
g(z)趋于0, 因为

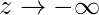
g(z)始终在0到1之间

因此, 现在, 我们可以为2个标签(0和1)定义条件概率

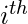
观察为：

我们可以更紧凑地编写为：

现在, 我们定义另一个术语,

参数的可能性

如：

给定一个模型和特定的参数值(此处为), 似然率不过是数据的概率(训练示例)。它针对的每个可能值来衡量数据提供的支持。我们通过将所有给定值相乘来获得它。

为了简化计算, 我们采用

对数似然

:

成本函数

对数回归与参数似然性成反比。因此, 我们可以使用对数似然方程来获得成本函数J的表达式：

我们的目的是估计

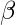
从而使成本函数最小化！

使用梯度下降算法

首先, 我们取

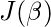
每一个

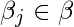
导出随机梯度下降规则(此处仅显示最终的导出值)：

在此, y和h(x)分别表示响应向量和预测响应向量。也,

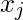
是代表观测值的向量

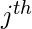
特征。

现在, 为了得到最小

,

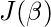
其中

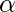
叫做

学习率

并且需要明确设置。

让我们在样本数据集上查看上述技术的python实现(从以下位置下载)

这里

)：

2.25 2.50 2.75 3.00 3.25 3.50 3.75 4.00 4.25 4.50 4.75 5.00 5.50

import csv
import numpy as np
import matplotlib.pyplot as plt
  
  
def loadCSV(filename):
     '''
     function to load dataset
     '''
     with open (filename, "r" ) as csvfile:
         lines = csv.reader(csvfile)
         dataset = list (lines)
         for i in range ( len (dataset)):
             dataset[i] = [ float (x) for x in dataset[i]]     
     return np.array(dataset)
  
  
def normalize(X):
     '''
     function to normalize feature matrix, X
     '''
     mins = np. min (X, axis = 0 )
     maxs = np. max (X, axis = 0 )
     rng = maxs - mins
     norm_X = 1 - ((maxs - X) /rng)
     return norm_X
  
  
def logistic_func(beta, X):
     '''
     logistic(sigmoid) function
     '''
     return 1.0 /( 1 + np.exp( - np.dot(X, beta.T)))
  
  
def log_gradient(beta, X, y):
     '''
     logistic gradient function
     '''
     first_calc = logistic_func(beta, X) - y.reshape(X.shape[ 0 ], - 1 )
     final_calc = np.dot(first_calc.T, X)
     return final_calc
  
  
def cost_func(beta, X, y):
     '''
     cost function, J
     '''
     log_func_v = logistic_func(beta, X)
     y = np.squeeze(y)
     step1 = y * np.log(log_func_v)
     step2 = ( 1 - y) * np.log( 1 - log_func_v)
     final = - step1 - step2
     return np.mean(final)
  
  
def grad_desc(X, y, beta, lr = . 01 , converge_change = . 001 ):
     '''
     gradient descent function
     '''
     cost = cost_func(beta, X, y)
     change_cost = 1
     num_iter = 1
      
     while (change_cost> converge_change):
         old_cost = cost
         beta = beta - (lr * log_gradient(beta, X, y))
         cost = cost_func(beta, X, y)
         change_cost = old_cost - cost
         num_iter + = 1
      
     return beta, num_iter 
  
  
def pred_values(beta, X):
     '''
     function to predict labels
     '''
     pred_prob = logistic_func(beta, X)
     pred_value = np.where(pred_prob> = . 5 , 1 , 0 )
     return np.squeeze(pred_value)
  
  
def plot_reg(X, y, beta):
     '''
     function to plot decision boundary
     '''
     # labelled observations
     x_0 = X[np.where(y = = 0.0 )]
     x_1 = X[np.where(y = = 1.0 )]
      
     # plotting points with diff color for diff label
     plt.scatter([x_0[:, 1 ]], [x_0[:, 2 ]], c = 'b' , label = 'y = 0' )
     plt.scatter([x_1[:, 1 ]], [x_1[:, 2 ]], c = 'r' , label = 'y = 1' )
      
     # plotting decision boundary
     x1 = np.arange( 0 , 1 , 0.1 )
     x2 = - (beta[ 0 , 0 ] + beta[ 0 , 1 ] * x1) /beta[ 0 , 2 ]
     plt.plot(x1, x2, c = 'k' , label = 'reg line' )
  
     plt.xlabel( 'x1' )
     plt.ylabel( 'x2' )
     plt.legend()
     plt.show()
      
  
      
if __name__ = = "__main__" :
     # load the dataset
     dataset = loadCSV( 'dataset1.csv' )
      
     # normalizing feature matrix
     X = normalize(dataset[:, : - 1 ])
      
     # stacking columns wth all ones in feature matrix
     X = np.hstack((np.matrix(np.ones(X.shape[ 0 ])).T, X))
  
     # response vector
     y = dataset[:, - 1 ]
  
     # initial beta values
     beta = np.matrix(np.zeros(X.shape[ 1 ]))
  
     # beta values after running gradient descent
     beta, num_iter = grad_desc(X, y, beta)
  
     # estimated beta values and number of iterations
     print ( "Estimated regression coefficients:" , beta)
     print ( "No. of iterations:" , num_iter)
  
     # predicted labels
     y_pred = pred_values(beta, X)
      
     # number of correctly predicted labels
     print ( "Correctly predicted labels:" , np. sum (y = = y_pred))
      
     # plotting regression line
     plot_reg(X, y, beta)

Estimated regression coefficients: [[  1.70474504  15.04062212 -20.47216021]]
No. of iterations: 2612
Correctly predicted labels: 100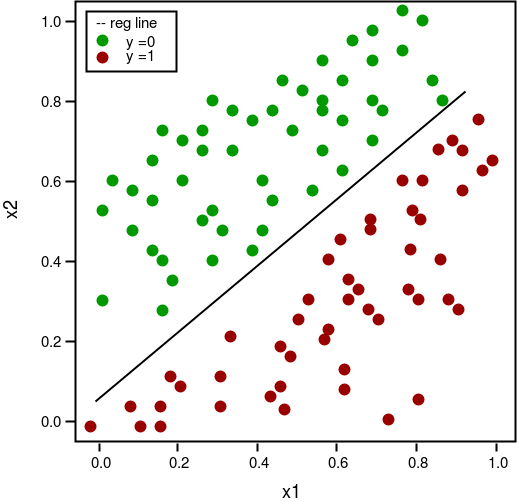

注意：梯度下降是多种估算方法之一

.

基本上, 这些是更高级的算法, 一旦你定义了成本函数和梯度, 就可以轻松地在Python中运行。这些算法是：

• BFGS(Broyden–Fletcher–Goldfarb–Shanno算法)
• L-BFGS(类似于BFGS, 但使用的内存有限)
• 共轭梯度

与梯度下降相比, 使用这些算法中的任何一种的优点/缺点：

• 优点
  • 不需要选择学习率
  • 通常运行得更快(并非总是如此)
  • 可以从数字上为你近似渐变(不一定总是很好)
• 缺点
  • 更复杂
  • 除非你了解细节, 否则更多是黑匣子

多项式Logistic回归

在多项式Logistic回归中, 输出变量可以具有

超过两个可能的离散输出

。考虑一下

数字数据集

。在此, 输出变量是数字值, 可以取不到(0、12、3、4、5、6、7、8、9)中的值。

下面给出了使用scikit-learn对数字数据集进行预测的多项式Logisitc回归的实现。

from sklearn import datasets, linear_model, metrics
   
# load the digit dataset
digits = datasets.load_digits()
   
# defining feature matrix(X) and response vector(y)
X = digits.data
y = digits.target
  
# splitting X and y into training and testing sets
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.4 , random_state = 1 )
   
# create logistic regression object
reg = linear_model.LogisticRegression()
   
# train the model using the training sets
reg.fit(X_train, y_train)
  
# making predictions on the testing set
y_pred = reg.predict(X_test)
   
# comparing actual response values (y_test) with predicted response values (y_pred)
print ( "Logistic Regression model accuracy(in %):" , metrics.accuracy_score(y_test, y_pred) * 100 )

Logistic Regression model accuracy(in %): 95.6884561892

最后, 需要考虑以下有关Logistic回归的要点：

• 不假设因变量和自变量之间存在线性关系, 但确实假设解释变量的对数和响应.
• 自变量甚至可以是原始自变量的幂项或其他一些非线性变换。
• 因变量不需要是正态分布的, 但通常假定它是来自指数族的分布(例如, 二项式, 泊松, 多项式, 正态等)；二元逻辑回归假设响应的二项式分布。
• 不需要满足方差的均匀性。
• 错误必须是独立的, 但不能正态分布。
• 它使用最大似然估计(MLE)而不是普通最小二乘法(OLS)来估计参数, 因此依赖于大样本近似.

参考文献：

• http://cs229.stanford.edu/notes/cs229-notes1.pdf
• http://lsbin.com/logistic-regression-for-machine-learning/
• https://onlinecourses.science.psu.edu/stat504/node/164

如果发现任何不正确的地方, 或者想分享有关上述主题的更多信息, 请写评论。

注意怪胎！巩固你的基础Python编程基础课程和学习基础知识。

首先, 你的面试准备可通过以下方式增强你的数据结构概念：Python DS课程。