快速排序与合并排序有什么区别？

快速分类是基于分而治之策略的内部算法。在此：

• 元素数组被重复地分成多个部分, 直到无法进一步划分为止。
• 也被称为"分区交换排序".
• 它使用关键元素(枢轴)对元素进行分区。
• 一个左分区包含所有小于枢轴的元素, 而一个右分区包含所有大于键元素的元素。

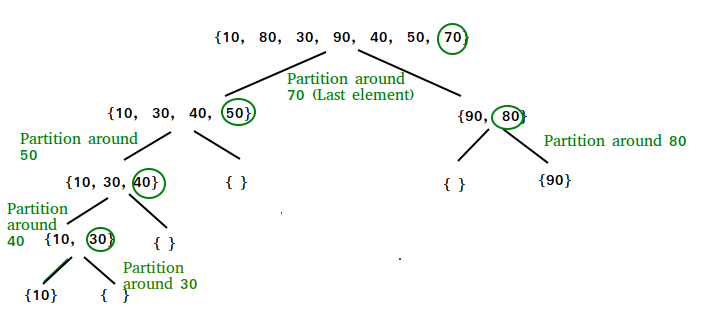
合并排序是一种外部算法, 基于分而治之策略。在此：

• 元素一次又一次地分成两个子数组(n / 2), 直到只剩下一个元素为止。
• 合并排序使用其他存储对辅助阵列进行排序。
• 合并排序使用三个数组, 其中两个用于存储每个一半, 第三个外部一个用于通过合并其他两个来存储最终的排序列表, 然后对每个数组进行递归排序。
• 最后, 合并所有子数组, 使其成为该元素的" n"个元素大小。

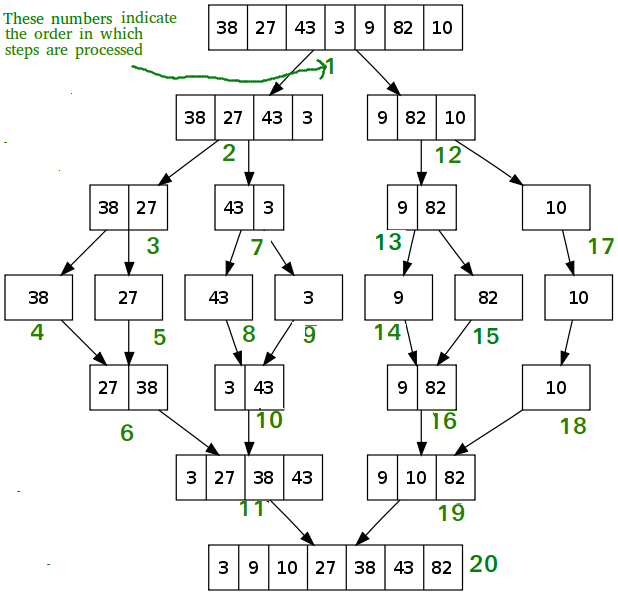
快速排序与合并排序

1. 数组中元素的分区:
   在合并排序中, 数组仅分成两半(即n / 2)。
   而
   在快速排序的情况下, 数组可以分成任意比例。没有强迫将元素数组快速分类为相等的部分。
2. 最坏情况下的复杂性:
   快速分类的最坏情况复杂度为O(n2), 因为在最坏情况下需要进行大量比较。
   而
   在合并排序中, 最坏情况和平均情况具有相同的复杂度O(n log n)。
3. 数据集的用法:
   合并排序可以在任何类型的数据集上正常工作, 而不论其大小(大小)。
   而
   快速排序不适用于大型数据集。
4. 额外的存储空间要求:
   合并排序没有到位, 因为它需要额外的内存空间来存储辅助阵列。
   而
   快速排序已经到位, 因为它不需要任何其他存储空间。
5. 效率:
   在较大数组大小或数据集的情况下, 合并排序比快速排序更有效且工作更快。
   而
   在较小的数组或数据集的情况下, 快速排序比合并排序更有效且工作更快。
6. 排序方式:
   快速排序是内部排序方法, 其中数据在主内存中排序。
   而
   合并排序是一种外部排序方法, 其中要排序的数据无法容纳在内存中, 并且无法使用需要的辅助内存进行排序。
7. 稳定性:
   合并排序是稳定的, 因为具有相等值的两个元素在排序输出中的顺序与输入未排序数组中的顺序相同。
   而
   在这种情况下, 快速排序是不稳定的。但是可以通过对代码进行一些更改来使其稳定。
8. 首选:
   快速排序是数组的首选。
   而
   合并排序是链接列表的首选。
9. 参考地点:
   Quicksort具有良好的缓存局部性, 这使Quicksort比合并排序更快(在许多情况下, 例如在虚拟内存环境中)。

比较依据	快速排序	合并排序
数组中元素的分区	元素数组的分割比例不限, 不一定要一半。	元素数组的分割比例不限, 不一定要一半。
最坏情况下的复杂性	O(n2)	O(登录)
运作良好	它在较小的阵列上效果很好	它可以在任何大小的阵列上正常运行
执行速度	对于小数据集(例如选择排序等), 它比其他排序算法更快地工作	在任何大小的数据上都具有一致的速度
额外的存储空间要求	较少(就地)	更多(非就地)
效率	对于较大的阵列效率低下	更高效
排序方式	内部	外部
稳定性	不稳定	稳定
首选	用于数组	用于链接列表
参考地点	好	较差的

---