算法设计：布尔括号问题| DP-37

2021年4月17日18:30:23 发表评论 1,415 次浏览

本文概述

给定带有以下符号的布尔表达式。

Symbols
    'T' ---> true 
    'F' ---> false

并在符号之间填充以下运算符

Operators
    &   ---> boolean AND
    |   ---> boolean OR
    ^   ---> boolean XOR

计算可以在表达式中加上括号的方式的数目, 以便使表达式的值评估为true。

让输入为两个数组的形式, 一个包含顺序的符号(T和F), 另一个包含运算符(＆, |和^}

例子：

Input: symbol[]    = {T, F, T}
       operator[]  = {^, &}
Output: 2
The given expression is "T ^ F & T", it evaluates true
in two ways "((T ^ F) & T)" and "(T ^ (F & T))"

Input: symbol[]    = {T, F, F}
       operator[]  = {^, |}
Output: 2
The given expression is "T ^ F | F", it evaluates true
in two ways "( (T ^ F) | F )" and "( T ^ (F | F) )". 

Input: symbol[]    = {T, T, F, T}
       operator[]  = {|, &, ^}
Output: 4
The given expression is "T | T & F ^ T", it evaluates true
in 4 ways ((T|T)&(F^T)), (T|(T&(F^T))), (((T|T)&F)^T) 
and (T|((T&F)^T)).

解：

让T(i, j)>表示在i和j之间(包括两端)加上括号的方式的数量, 以使i和j之间的子表达式求值为true。

T（i，j）= \ sum_ {k = i} ^ {j-1} \ begin {Bmatrix} T（i，k）* T（k + 1，j）＆if＆operator＆[k]是'\＆' \\总计（i，k）*总计（k + 1，j）-F（i，k）* F（k + 1，j）＆if＆operator＆[k]＆is'|' \\ T（i，k）* F（k + 1，j）+ F（i，k）* T（k + 1，j）＆if＆operator＆[k]＆is'\ oplus'\ end {Bmatrix}总计（i ，j）= T（i，j）+ F（i，j）

<！–

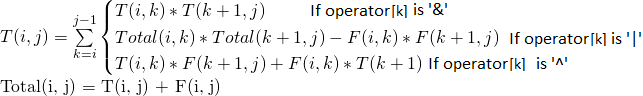
Trueeq

–>

让F(i, j)表示在i和j之间(包括两端)加上括号的方式的数量, 以使i和j之间的子表达式求值为false。

F（i，j）= \ sum_ {k = i} ^ {j-1} \ begin {Bmatrix} Total（i，k）*总计（k + 1，j）-T（i，k）* T（ k + 1，j）＆if＆operator [k]＆is'\＆'\\ F（i，k）* F（k + 1，j）＆if＆operator [k]＆is'|' \\ T（i，k）* T（k + 1，j）+ F（i，k）* F（k + 1，j）＆if＆operator [k]＆is'\ oplus'\ end {Bmatrix} Total（i ，j）= T（i，j）+ F（i，j）

<！—

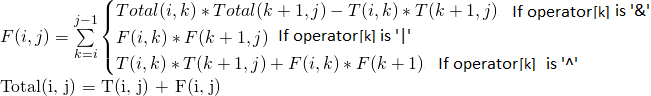
falseeq

–>

基本案例：

T(i, i) = 1 if symbol[i] = 'T' 
T(i, i) = 0 if symbol[i] = 'F' 

F(i, i) = 1 if symbol[i] = 'F' 
F(i, i) = 0 if symbol[i] = 'T'

如果我们绘制上述递归解的递归树, 则可以观察到它有许多重叠的子问题。像其他动态规划问题, 可以通过自下而上的方式填充表格来解决。以下是动态编程解决方案的C++实现。

C ++

#include<iostream>
#include<cstring>
using namespace std;
  
//Returns count of all possible parenthesizations that lead to
//result true for a boolean expression with symbols like true
//and false and operators like &, | and ^ filled between symbols
int countParenth( char symb[], char oper[], int n)
{
     int F[n][n], T[n][n];
  
     //Fill diaginal entries first
     //All diagonal entries in T[i][i] are 1 if symbol[i]
     //is T (true).  Similarly, all F[i][i] entries are 1 if
     //symbol[i] is F (False)
     for ( int i = 0; i <n; i++)
     {
         F[i][i] = (symb[i] == 'F' )? 1: 0;
         T[i][i] = (symb[i] == 'T' )? 1: 0;
     }
  
     //Now fill T[i][i+1], T[i][i+2], T[i][i+3]... in order
     //And F[i][i+1], F[i][i+2], F[i][i+3]... in order
     for ( int gap=1; gap<n; ++gap)
     {
         for ( int i=0, j=gap; j<n; ++i, ++j)
         {
             T[i][j] = F[i][j] = 0;
             for ( int g=0; g<gap; g++)
             {
                 //Find place of parenthesization using current value
                 //of gap
                 int k = i + g;
  
                 //Store Total[i][k] and Total[k+1][j]
                 int tik = T[i][k] + F[i][k];
                 int tkj = T[k+1][j] + F[k+1][j];
  
                 //Follow the recursive formulas according to the current
                 //operator
                 if (oper[k] == '&' )
                 {
                     T[i][j] += T[i][k]*T[k+1][j];
                     F[i][j] += (tik*tkj - T[i][k]*T[k+1][j]);
                 }
                 if (oper[k] == '|' )
                 {
                     F[i][j] += F[i][k]*F[k+1][j];
                     T[i][j] += (tik*tkj - F[i][k]*F[k+1][j]);
                 }
                 if (oper[k] == '^' )
                 {
                     T[i][j] += F[i][k]*T[k+1][j] + T[i][k]*F[k+1][j];
                     F[i][j] += T[i][k]*T[k+1][j] + F[i][k]*F[k+1][j];
                 }
             }
         }
     }
     return T[0][n-1];
}
  
//Driver program to test above function
int main()
{
     char symbols[] = "TTFT" ;
     char operators[] = "|&^" ;
     int n = strlen (symbols);
  
     //There are 4 ways
     //((T|T)&(F^T)), (T|(T&(F^T))), (((T|T)&F)^T) and (T|((T&F)^T))
     cout <<countParenth(symbols, operators, n);
     return 0;
}

Java

class GFG 
{
      
     //Returns count of all possible 
     //parenthesizations that lead to
     //result true for a boolean 
     //expression with symbols like true
     //and false and operators like &, | 
     //and ^ filled between symbols
     static int countParenth( char symb[], char oper[], int n)    
     {
         int F[][] = new int [n][n];
         int T[][] = new int [n][n];
  
         //Fill diaginal entries first
         //All diagonal entries in T[i][i] 
         //are 1 if symbol[i] is T (true). 
         //Similarly, all F[i][i] entries 
         //are 1 if symbol[i] is F (False)
         for ( int i = 0 ; i <n; i++) 
         {
             F[i][i] = (symb[i] == 'F' ) ? 1 : 0 ;
             T[i][i] = (symb[i] == 'T' ) ? 1 : 0 ;
         }
  
         //Now fill T[i][i+1], T[i][i+2], //T[i][i+3]... in order And F[i][i+1], //F[i][i+2], F[i][i+3]... in order
         for ( int gap = 1 ; gap <n; ++gap)
         {
             for ( int i = 0 , j = gap; j <n; ++i, ++j) 
             {
                 T[i][j] = F[i][j] = 0 ;
                 for ( int g = 0 ; g <gap; g++) 
                 {
                     //Find place of parenthesization 
                     //using current value of gap
                     int k = i + g;
  
                     //Store Total[i][k] and Total[k+1][j]
                     int tik = T[i][k] + F[i][k];
                     int tkj = T[k + 1 ][j] + F[k + 1 ][j];
  
                     //Follow the recursive formulas 
                     //according to the current operator
                     if (oper[k] == '&' ) 
                     {
                         T[i][j] += T[i][k] * T[k + 1 ][j];
                         F[i][j] += (tik * tkj - T[i][k] * T[k + 1 ][j]);
                     }
                     if (oper[k] == '|' ) 
                     {
                         F[i][j] += F[i][k] * F[k + 1 ][j];
                         T[i][j] += (tik * tkj - F[i][k] * F[k + 1 ][j]);
                     }
                     if (oper[k] == '^' )
                     {
                         T[i][j] += F[i][k] * T[k + 1 ][j] + 
                                     T[i][k] * F[k + 1 ][j];
                         F[i][j] += T[i][k] * T[k + 1 ][j] + 
                                     F[i][k] * F[k + 1 ][j];
                     }
                 }
             }
         }
         return T[ 0 ][n - 1 ];
     }
  
     //Driver code
     public static void main(String[] args) 
     {
         char symbols[] = "TTFT" .toCharArray();
         char operators[] = "|&^" .toCharArray();
         int n = symbols.length;
  
         //There are 4 ways
         //((T|T)&(F^T)), (T|(T&(F^T))), //(((T|T)&F)^T) and (T|((T&F)^T))
         System.out.println(countParenth(symbols, operators, n));
     }
}
  
//This code has been contributed 
//by 29AjayKumar

Python3

# Returns count of all possible 
# parenthesizations that lead to 
# result true for a boolean 
# expression with symbols like  
# true and false and operators 
# like &, | and ^ filled between symbols 
def countParenth(symb, oper, n):
     F = [[ 0 for i in range (n + 1 )] 
             for i in range (n + 1 )]
     T = [[ 0 for i in range (n + 1 )] 
             for i in range (n + 1 )]
              
     # Fill diaginal entries first 
     # All diagonal entries in 
     # T[i][i] are 1 if symbol[i] 
     # is T (true). Similarly, all
     # F[i][i] entries are 1 if 
     # symbol[i] is F (False) 
     for i in range (n):
         if symb[i] = = 'F' :
             F[i][i] = 1
         else :
             F[i][i] = 0
  
         if symb[i] = = 'T' :
             T[i][i] = 1
         else :
             T[i][i] = 0
              
     # Now fill T[i][i+1], T[i][i+2], # T[i][i+3]... in order And 
     # F[i][i+1], F[i][i+2], # F[i][i+3]... in order
     for gap in range ( 1 , n):
         i = 0
         for j in range (gap, n): 
             T[i][j] = F[i][j] = 0
             for g in range (gap):
                  
                 # Find place of parenthesization 
                 # using current value of gap
                 k = i + g
                  
                 # Store Total[i][k] and Total[k+1][j] 
                 tik = T[i][k] + F[i][k]; 
                 tkj = T[k + 1 ][j] + F[k + 1 ][j];
                  
                 # Follow the recursive formulas 
                 # according to the current operator
                 if oper[k] = = '&' :
                     T[i][j] + = T[i][k] * T[k + 1 ][j]
                     F[i][j] + = (tik * tkj - T[i][k] * 
                                             T[k + 1 ][j])
                 if oper[k] = = '|' :
                     F[i][j] + = F[i][k] * F[k + 1 ][j]
                     T[i][j] + = (tik * tkj - F[i][k] * 
                                             F[k + 1 ][j])
                 if oper[k] = = '^' :
                     T[i][j] + = (F[i][k] * T[k + 1 ][j] + 
                                 T[i][k] * F[k + 1 ][j]) 
                     F[i][j] + = (T[i][k] * T[k + 1 ][j] + 
                                 F[i][k] * F[k + 1 ][j])
             i + = 1
     return T[ 0 ][n - 1 ] 
      
# Driver Code
symbols = "TTFT"
operators = "|&^"
n = len (symbols)
  
# There are 4 ways 
# ((T|T)&(F^T)), (T|(T&(F^T))), # (((T|T)&F)^T) and (T|((T&F)^T)) 
print (countParenth(symbols, operators, n))
  
# This code is contributed by 
# sahil shelangia

C#

//C# program of above approach
using System;
  
class GFG 
{
      
     //Returns count of all possible 
     //parenthesizations that lead to
     //result true for a boolean 
     //expression with symbols like true
     //and false and operators like &, | 
     //and ^ filled between symbols
     static int countParenth( char []symb, char []oper, int n) 
     {
         int [, ]F = new int [n, n];
         int [, ]T = new int [n, n];
  
         //Fill diaginal entries first
         //All diagonal entries in T[i, i] 
         //are 1 if symbol[i] is T (true). 
         //Similarly, all F[i, i] entries 
         //are 1 if symbol[i] is F (False)
         for ( int i = 0; i <n; i++) 
         {
             F[i, i] = (symb[i] == 'F' ) ? 1 : 0;
             T[i, i] = (symb[i] == 'T' ) ? 1 : 0;
         }
  
         //Now fill T[i, i+1], T[i, i+2], //T[i, i+3]... in order And F[i, i+1], //F[i, i+2], F[i, i+3]... in order
         for ( int gap = 1; gap <n; ++gap)
         {
             for ( int i = 0, j = gap; j <n; ++i, ++j) 
             {
                 T[i, j] = F[i, j] = 0;
                 for ( int g = 0; g <gap; g++) 
                 {
                     //Find place of parenthesization 
                     //using current value of gap
                     int k = i + g;
  
                     //Store Total[i, k] and Total[k+1, j]
                     int tik = T[i, k] + F[i, k];
                     int tkj = T[k + 1, j] + F[k + 1, j];
  
                     //Follow the recursive formulas 
                     //according to the current operator
                     if (oper[k] == '&' ) 
                     {
                         T[i, j] += T[i, k] * T[k + 1, j];
                         F[i, j] += (tik * tkj - T[i, k] * T[k + 1, j]);
                     }
                     if (oper[k] == '|' ) 
                     {
                         F[i, j] += F[i, k] * F[k + 1, j];
                         T[i, j] += (tik * tkj - F[i, k] * F[k + 1, j]);
                     }
                     if (oper[k] == '^' )
                     {
                         T[i, j] += F[i, k] * T[k + 1, j] + 
                                     T[i, k] * F[k + 1, j];
                         F[i, j] += T[i, k] * T[k + 1, j] + 
                                     F[i, k] * F[k + 1, j];
                     }
                 }
             }
         }
         return T[0, n - 1];
     }
  
     //Driver code
     public static void Main() 
     {
         char []symbols = "TTFT" .ToCharArray();
         char []operators = "|&^" .ToCharArray();
         int n = symbols.Length;
  
         //There are 4 ways
         //((T|T)&(F^T)), (T|(T&(F^T))), //(((T|T)&F)^T) and (T|((T&F)^T))
         Console.WriteLine(countParenth(symbols, operators, n));
     }
}
  
/* This code contributed by PrinciRaj1992 */

输出如下：

4

时间复杂度：O(n^3)

辅助空间：O(n^2)

参考文献：

http://people.cs.clemson.edu/~bcdean/dp_practice/dp_9.swf

如果发现任何不正确的地方, 或者想分享有关上述主题的更多信息, 请发表评论。

木子山

发表评论

:?: :razz: :sad: :evil: :!: :smile: :oops: :grin: :eek: :shock: :???: :cool: :lol: :mad: :twisted: :roll: :wink: :idea: :arrow: :neutral: :cry: :mrgreen: