登山简介|人工智能

爬山是一种启发式搜索, 用于人工智能领域中的数学优化问题。

给定大量输入和良好的启发式功能, 它会尝试找到足够好的解决问题的方法。该解决方案可能不是全局最优最大值。

• 在以上定义中, 数学优化问题这意味着爬山解决了我们需要通过从给定输入中选择值来最大化或最小化给定实函数的问题。例-旅行商问题我们需要尽量减少推销员的旅行距离。
• "启发式搜索"表示该搜索算法可能找不到该问题的最佳解决方案。但是, 它将提供一个很好的解决方案合理的时间。
• 一种启发式功能是一项功能, 可根据可用信息在搜索算法的任何分支步骤中对所有可能的替代方案进行排名。它有助于算法从可能的路线中选择最佳路线。

爬山的特点

1. 生成和测试算法的变体：它是生成和测试算法的变体。生成和测试算法如下：

1.生成可能的解决方案。
2.测试以查看这是否是预期的解决方案。
3.如果找到解决方案, 请退出, 否则转到步骤1。

因此, 我们将爬山称为生成和测试算法的变体, 因为它从测试过程中获取反馈。然后, 生成器将利用此反馈来确定搜索空间中的下一个动作。

2. 使用贪婪方法: 在状态空间中的任何点, 搜索都只朝那个方向移动, 这会优化功能成本, 并希望最终找到最佳解决方案。

爬山的类型

简单爬山：它逐个检查相邻节点, 然后选择优化当前成本的第一个相邻节点作为下一个节点。

简单爬山算法:

步骤1：评估初始状态。如果是目标状态, 则停止并返回成功。否则, 将初始状态设为当前状态。
步骤2：循环直到找到解决方案状态, 或者不存在可以应用于当前状态的新运算符。
a)选择一个尚未应用到当前状态的状态, 并将其应用以产生新状态。
b)执行这些操作以评估新状态
i。如果当前状态是目标状态, 则停止并返回成功。
ii。如果它比当前状态更好, 则使其成为当前状态并继续进行。
iii。如果不是比当前状态更好, 则继续循环直到找到解决方案。步骤3：退出。

最陡坡登山：它首先检查所有相邻节点, 然后从下一个节点中选择最接近解决方案状态的节点。

步骤1：评估初始状态。如果是目标状态, 则退出, 否则将当前状态设为初始状态。步骤2：重复这些步骤, 直到找到解决方案或当前状态不变。假设"目标"为一种状态, 以使当前状态的任何后继者都比它更好。 ii。对于适用于当前状态的每个运算符应用新运算符并创建新状态b。评估新状态c。如果此状态为目标状态, 则退出, 否则与"目标"进行比较。如果此状态优于"目标", 则将此状态设置为"目标" e。如果目标优于当前状态, 则将当前状态设置为目标步骤3：退出

随机爬山：

在决定选择哪个节点之前, 它不会检查所有相邻节点。它只是随机选择一个相邻节点, 然后(基于该邻居的改进量)决定是移至该邻居还是要检查另一个。

爬山状态空间图

状态空间图是我们的搜索算法可以达到的状态集与目标函数(我们希望最大化的函数)的值的图形表示。

X轴：表示状态空间, 即我们的算法可能达到的状态或配置。

Y轴：表示对应于特定状态的目标函数的值。

最好的解决方案是目标函数具有最大值(全局最大值)的状态空间。

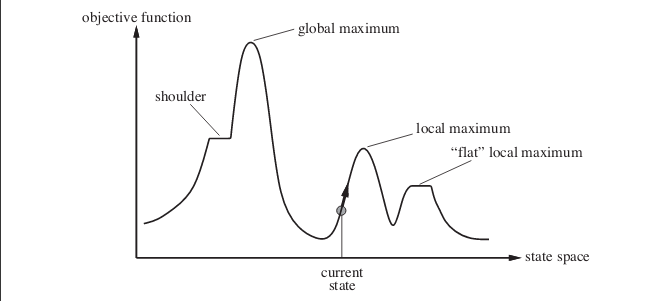
状态空间图中的不同区域

1. 局部最大值：它是一个比其相邻状态更好的状态, 但是存在一个比其相邻状态更好的状态(全局最大值)。此状态更好, 因为此处目标函数的值高于其邻居函数的值。
2. 全局最大值：这是状态空间图中最好的状态。这是因为在这种状态下, 目标函数具有最高的价值。
3. 高原/平坦局部最大值：它是状态空间的平坦区域, 其中相邻状态具有相同的值。
4. 山脊它是一个比邻国高但本身有坡度的区域。这是一种特殊的局部最大值。
5. 当前状态 ：搜索期间我们当前所在的状态空间图区域。
6. 肩宽：这是一个上坡的高原。

登山中不同地区的问题

如果爬山进入以下任何区域, 则无法达到最佳/最佳状态(全局最大值)：

局部最大值：在局部最大值处, 所有相邻状态的值都比当前状态差。由于爬山使用贪婪的方法, 因此爬山不会移动到更糟的状态并自行终止。即使可能存在更好的解决方案, 该过程也将结束。

要克服局部最大问题：利用回溯技术。维护访问状态列表。如果搜索达到不良状态, 则可以回溯到先前的配置并探索新路径。

高原：在高原上, 所有邻居都具有相同的价值。因此, 不可能选择最佳方向。

克服高原：大跃进。随机选择一个远离当前状态的状态。我们很可能会降落在非高原地区山脊

脊上的任何点都可能看起来像峰, 因为在所有可能的方向上的移动都是向下的。因此, 算法在达到此状态时停止。

克服岭：

在这种障碍下, 请在测试前使用两个或多个规则。它意味着一次向多个方向移动。

---