算法分析：构建堆的时间复杂度介绍

考虑以下用于构建输入数组A的堆的算法。

BUILD-HEAP(A) 
    heapsize := size(A); 
    for i := floor(heapsize/2) downto 1 
        do HEAPIFY(A, i); 
    end for 
END

快速浏览以上算法, 表明运行时间为

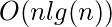
, 因为每Heapify代价为

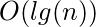
和构建堆使

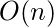
这样的调用。

这个上限虽然正确, 但不是渐近严格的。

我们可以通过观察Heapify的运行时间取决于树' h '的高度(它等于lg(n)，其中n是节点的数量)，而大多数子树的高度都很小，从而得出一个更紧密的界限。

高度h随着我们沿着树向上移动而增加。Build-Heap的第3行运行一个循环，从高度为1的最后一个内部节点(heapsize/2)的索引，到高度为lg(n)的根(1)的索引。因此，Heapify对每个节点花费的时间不同，即

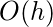
为了找到构建堆的时间复杂度，我们必须知道高度为h的节点的数量。

为此, 我们使用一个事实, 即大小为n的堆最多具有

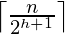
高度为h的节点。

现在, 为了推导时间复杂度, 我们表示构建堆如-

(1)

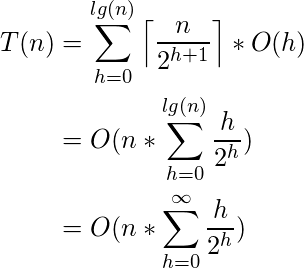
第2步使用Big-Oh表示法的属性来忽略上限函数和常数2(

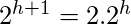
)。同样, 在第三步中, 由于我们使用的是Big-Oh表示法, 因此可以将求和的上限增加到无穷大。

无限G.P. (x <1)

(2)

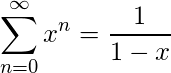
在微分两边并乘以x时, 我们得到

(3)

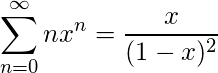
将(3)中获得的结果放回我们的推导(1)中, 我们得到

(4)

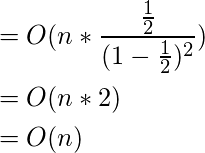
因此证明了构建二进制堆的时间复杂度为

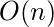
参考：

http://www.cs.sfu.ca/CourseCentral/307/petra/2009/SLN_2.pdf

如果发现任何不正确的地方, 或者想分享有关上述主题的更多信息, 请写评论。