概率统计|辛普森悖论（加州大学伯克利分校的诉讼）

辛普森悖论用外行的术语来说, 就是将那些子组数据合并后, 数据内部相对于子组的关系反转。

例如, 如果一所大学中有两个部门, 并且两个部门都有很高的女性被录取的可能性, 那么根据直觉组合其数据后, 女性的整体录取概率应该很高, 但这可能不是事实。

数学上

给定a1/b1 <c1/d1并且a2/b2 <c2/d2那么(a1 + a2)/(b1 + b2)<(c1 + c2)/(d1 + d2)？

辛普森悖论说, 这可能不是真的。

7/8 <2/2 and 1/2 <5/8 yet, (7+1)/(2+2)> (2+5)/(2+8)

在针对加州大学伯克利分校的招生数据诉讼中也看到了类似的案例, 该数据显示, 与女性申请相比, 男性获得申请被接受的可能性更高。但是, 在检查了各个部门之后, 考虑了一个相反的情况, 因为最多的部门都偏爱女性而不是男性。

	申请者	已录取
男	8442	44%
女	4321	35%

部门	男	女
申请者	已录取	申请者	已录取
A	825	62%	108	82%
B	560	63%	25	68%
C	325	37%	593	34%
D	417	33%	375	35%
E	191	28%	393	24%
F	272	6%	341	7%

为什么会这样?

原因：

之所以会出现这种现象，是因为更多的女性申请竞争激烈、录取率低的部门，而更多的男性申请竞争不那么激烈、录取率高的部门。

从表中可以看出, 在高录取率部门中, 有825名男性申请, 而108名女性申请了一种。而更多的女孩正在诸如F和F。最终导致大学录取的男性人数多于女性。

另一个例子：

假设我们有一个如下图所示的配置, 绿色和蓝色两种类型的豆。

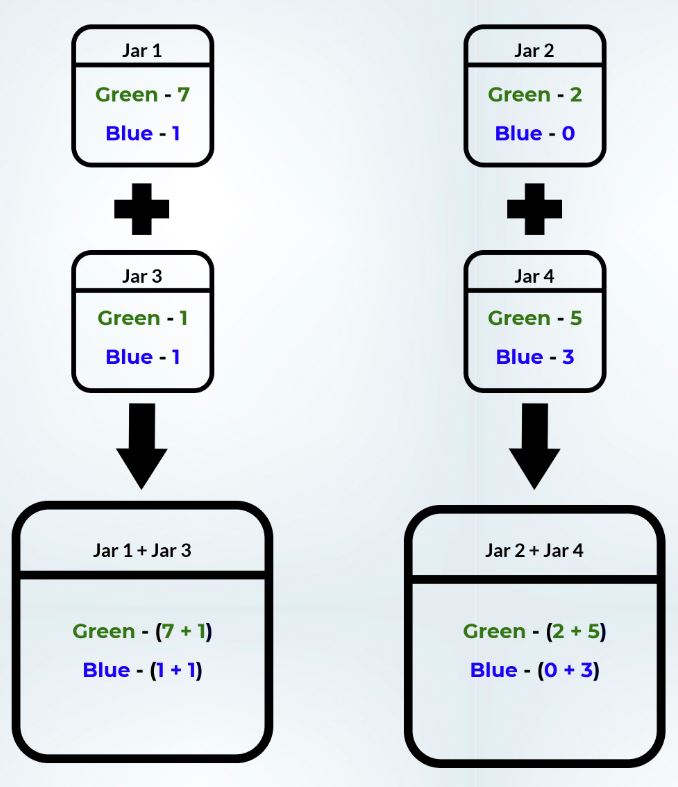
混合前：

从罐子里挑绿豆的可能性,

7/8      <   2/2
(Jar1)        (Jar2)

1/2      <   5/8
(Jar3)        (Jar4)

混合后：

从罐子里摘绿豆的可能性

8/10         >         7/10   Inequality
(Jar1 + Jar3)        (Jar2 + Jar4)

从这里我们还可以看到, 最初的罐子1和3分别比罐子2和罐子4采摘青豆的可能性更高, 但是在混合罐子的内容之后, 这种关系反过来了。混合后, Jar 2和Jar 4的合并含量有较高的机会采摘青豆。这是辛普森悖论的一个非常简单的例子。

---