算法题：雨水捕获问题介绍和解决

2021年4月16日19:06:07 发表评论 924 次浏览

本文概述

C++
Java
Python3
C++
Java
Python3
C#
的PHP
C++
Java
Python3
C#
的PHP
C++
Java
Python3
C++
Java

给定n个代表高程图的非负整数, 其中每个条的宽度为1, 计算下雨后它能捕集多少水。

例子:

Input: arr[]   = {2, 0, 2}
Output: 2
Explanation:
The structure is like below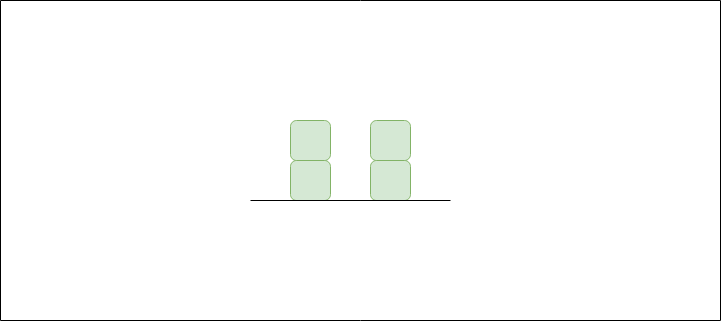

We can trap 2 units of water in the middle gap.

Input: arr[]   = {3, 0, 2, 0, 4}
Output: 7
Explanation:
Structure is like below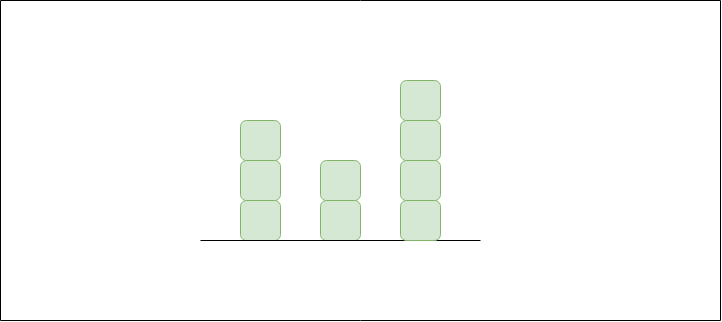

We can trap "3 units" of water between 3 and 2, "1 unit" on top of bar 2 and "3 units" between 2 
and 4.  See below diagram also.

Input: arr[] = [0, 1, 0, 2, 1, 0, 1, 3, 2, 1, 2, 1]
Output: 6

Explanation:
The structure is like below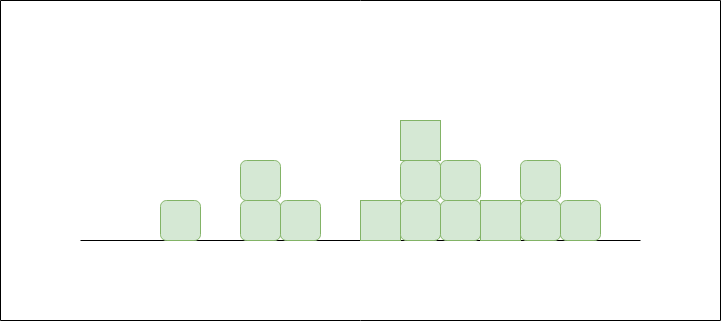

Trap "1 unit" between first 1 and 2, "4 units" between
first 2 and 3 and "1 unit" between second last 1 and last 2

基本思路：

如果左右两侧有较高的条形, 则数组的元素可以存储水。可以通过找到左侧和右侧条形的高度来找出要存储在每个元素中的水量。这个想法是计算可以存储在数组的每个元素中的水量。

例子

考虑数组{3, 0, 0, 2, 0, 4}, 可以存储三个单位的水三个索引1和2, 在索引3处存储一个水, 在索引4中存储三个水。

对于Array [] = {3, 0, 2, 0, 4}存储的水= 0 + 3 + 1 + 3 + 0 = 7

方法1：

这是解决上述问题的简单方法。

方法：这个想法是遍历每个数组元素, 并在左侧和右侧找到最高的条形。取两个高度中的较小者。当前元素的较小高度和高度之间的差是可以存储在此数组元素中的水量。
算法：
1. 从头到尾遍历数组。
2. 对于每个元素, 从开始到该索引遍历数组, 然后找到最大高度(一种)并从当前索引遍历数组到结尾并找到最大高度(b).
3. 将在此列中存储的水量为min(a, b)–数组[i], 将此值添加到存储的水总量中
4. 打印存储的水总量。
实现

C++

//C++ implementation of the approach
#include<bits/stdc++.h> 
using namespace std; 
  
//Function to return the maximum
//water that can be stored
int maxWater( int arr[], int n) 
{
      
     //To store the maximum water 
     //that can be stored
     int res = 0;
      
     //For every element of the array
     for ( int i = 1; i <n-1; i++) {
          
         //Find the maximum element on its left
         int left = arr[i];
         for ( int j=0; j<i; j++)
            left = max(left, arr[j]);
          
         //Find the maximum element on its right   
         int right = arr[i];
         for ( int j=i+1; j<n; j++)
            right = max(right, arr[j]); 
         
        //Update the maximum water    
        res = res + (min(left, right) - arr[i]);   
     }
  
     return res; 
} 
  
//Driver code
int main() 
{ 
     int arr[] = {0, 1, 0, 2, 1, 0, 1, 3, 2, 1, 2, 1}; 
     int n = sizeof (arr)/sizeof (arr[0]); 
      
     cout <<maxWater(arr, n); 
      
     return 0; 
}

Java

//Java implementation of the approach
class GFG{
  
//Function to return the maximum
//water that can be stored
public static int maxWater( int [] arr, int n) 
{
      
     //To store the maximum water
     //that can be stored
     int res = 0 ;
  
     //For every element of the array
     //except first and last element
     for ( int i = 1 ; i <n - 1 ; i++)
     {
          
         //Find maximum element on its left
         int left = arr[i];
         for ( int j = 0 ; j <i; j++)
         {
             left = Math.max(left, arr[j]);
         }
  
         //Find maximum element on its right
         int right = arr[i];
         for ( int j = i + 1 ; j <n; j++)
         {
             right = Math.max(right, arr[j]);
         }
  
         //Update maximum water value
         res += Math.min(left, right) - arr[i];
     }
     return res;
}
  
//Driver code
public static void main(String[] args)
{
     int [] arr = { 0 , 1 , 0 , 2 , 1 , 0 , 1 , 3 , 2 , 1 , 2 , 1 };
     int n = arr.length;
  
     System.out.print(maxWater(arr, n));
}
}
  
//This code is contributed by Debidutta Rath

Python3

# Python3 implementation of the approach 
  
# Function to return the maximum 
# water that can be stored 
def maxWater(arr, n) :
      
     # To store the maximum water 
     # that can be stored 
     res = 0 ; 
      
     # For every element of the array 
     for i in range ( 1 , n - 1 ) : 
          
         # Find the maximum element on its left 
         left = arr[i]; 
         for j in range (i) :
             left = max (left, arr[j]); 
          
         # Find the maximum element on its right 
         right = arr[i]; 
          
         for j in range (i + 1 , n) : 
             right = max (right, arr[j]);
              
         # Update the maximum water
         res = res + ( min (left, right) - arr[i]); 
  
     return res; 
  
# Driver code 
if __name__ = = "__main__" : 
  
     arr = [ 0 , 1 , 0 , 2 , 1 , 0 , 1 , 3 , 2 , 1 , 2 , 1 ]; 
     n = len (arr); 
      
     print (maxWater(arr, n)); 
      
# This code is contributed by AnkitRai01

输出如下：

复杂度分析：
- 时间复杂度：O(n^2)。
  有两个遍历数组的嵌套循环, 因此时间复杂度为O(n^2)。
- 空间复杂度：O(1)。
  不需要额外的空间。

方法2：

这是解决上述问题的有效方法。

方法：在先前的解决方案中, 要在左侧和右侧找到最高的条形, 需要遍历数组, 这会降低解决方案的效率。为了提高效率, 必须在线性时间内预先计算每个小节左右两边的最高小节。然后使用这些预先计算的值来查找每个数组元素中的水量。
算法：
1. 创建两个数组剩下和对大小为n。创建一个变量max_ = INT_MIN.
2. 从头到尾运行一个循环。在每次迭代中, 将max_更新为max_ = max(max_, arr [i])并分配左[i] = max_
3. 更新max_ = INT_MIN。
4. 从头到尾运行另一个循环。在每次迭代中, 将max_更新为max_ = max(max_, arr [i])并分配右[i] = max_
5. 从头到尾遍历数组。
6. 将在此列中存储的水量为min(a, b)–数组[i], (其中a =左[i], b =右[i])将此值加到存储的水总量中
7. 打印存储的水总量。
实现

C++

//C++ program to find maximum amount of water that can
//be trapped within given set of bars.
#include <bits/stdc++.h>
using namespace std;
  
int findWater( int arr[], int n)
{
     //left[i] contains height of tallest bar to the
     //left of i'th bar including itself
     int left[n];
  
     //Right [i] contains height of tallest bar to
     //the right of ith bar including itself
     int right[n];
  
     //Initialize result
     int water = 0;
  
     //Fill left array
     left[0] = arr[0];
     for ( int i = 1; i <n; i++)
         left[i] = max(left[i - 1], arr[i]);
  
     //Fill right array
     right[n - 1] = arr[n - 1];
     for ( int i = n - 2; i>= 0; i--)
         right[i] = max(right[i + 1], arr[i]);
  
     //Calculate the accumulated water element by element
     //consider the amount of water on i'th bar, the
     //amount of water accumulated on this particular
     //bar will be equal to min(left[i], right[i]) - arr[i] .
     for ( int i = 0; i <n; i++)
         water += min(left[i], right[i]) - arr[i];
  
     return water;
}
  
//Driver program
int main()
{
     int arr[] = { 0, 1, 0, 2, 1, 0, 1, 3, 2, 1, 2, 1 };
     int n = sizeof (arr) /sizeof (arr[0]);
     cout <<"Maximum water that can be accumulated is "
          <<findWater(arr, n);
     return 0;
}

Java

//Java program to find maximum amount of water that can
//be trapped within given set of bars.
  
class Test {
     static int arr[] = new int [] { 0 , 1 , 0 , 2 , 1 , 0 , 1 , 3 , 2 , 1 , 2 , 1 };
  
     //Method for maximum amount of water
     static int findWater( int n)
     {
         //left[i] contains height of tallest bar to the
         //left of i'th bar including itself
         int left[] = new int [n];
  
         //Right [i] contains height of tallest bar to
         //the right of ith bar including itself
         int right[] = new int [n];
  
         //Initialize result
         int water = 0 ;
  
         //Fill left array
         left[ 0 ] = arr[ 0 ];
         for ( int i = 1 ; i <n; i++)
             left[i] = Math.max(left[i - 1 ], arr[i]);
  
         //Fill right array
         right[n - 1 ] = arr[n - 1 ];
         for ( int i = n - 2 ; i>= 0 ; i--)
             right[i] = Math.max(right[i + 1 ], arr[i]);
  
         //Calculate the accumulated water element by element
         //consider the amount of water on i'th bar, the
         //amount of water accumulated on this particular
         //bar will be equal to min(left[i], right[i]) - arr[i] .
         for ( int i = 0 ; i <n; i++)
             water += Math.min(left[i], right[i]) - arr[i];
  
         return water;
     }
  
     //Driver method to test the above function
     public static void main(String[] args)
     {
  
         System.out.println( "Maximum water that can be accumulated is " + findWater(arr.length));
     }
}

Python3

# Python program to find maximum amount of water that can
# be trapped within given set of bars.
  
def findWater(arr, n):
  
     # left[i] contains height of tallest bar to the
     # left of i'th bar including itself
     left = [ 0 ] * n
  
     # Right [i] contains height of tallest bar to
     # the right of ith bar including itself
     right = [ 0 ] * n
  
     # Initialize result
     water = 0
  
     # Fill left array
     left[ 0 ] = arr[ 0 ]
     for i in range ( 1 , n):
         left[i] = max (left[i - 1 ], arr[i])
  
     # Fill right array
     right[n - 1 ] = arr[n - 1 ]
     for i in range (n - 2 , - 1 , - 1 ):
         right[i] = max (right[i + 1 ], arr[i]);
  
     # Calculate the accumulated water element by element
     # consider the amount of water on i'th bar, the
     # amount of water accumulated on this particular
     # bar will be equal to min(left[i], right[i]) - arr[i] .
     for i in range ( 0 , n):
         water + = min (left[i], right[i]) - arr[i]
  
     return water
  
  
# Driver program
  
arr = [ 0 , 1 , 0 , 2 , 1 , 0 , 1 , 3 , 2 , 1 , 2 , 1 ]
n = len (arr)
print ( "Maximum water that can be accumulated is" , findWater(arr, n))
  
# This code is contributed by
# Smitha Dinesh Semwal

C#

//C# program to find maximum amount of water that can
//be trapped within given set of bars.
using System;
  
class Test {
     static int [] arr = new int [] { 0, 1, 0, 2, 1, 0, 1, 3, 2, 1, 2, 1 };
  
     //Method for maximum amount of water
     static int findWater( int n)
     {
         //left[i] contains height of tallest bar to the
         //left of i'th bar including itself
         int [] left = new int [n];
  
         //Right [i] contains height of tallest bar to
         //the right of ith bar including itself
         int [] right = new int [n];
  
         //Initialize result
         int water = 0;
  
         //Fill left array
         left[0] = arr[0];
         for ( int i = 1; i <n; i++)
             left[i] = Math.Max(left[i - 1], arr[i]);
  
         //Fill right array
         right[n - 1] = arr[n - 1];
         for ( int i = n - 2; i>= 0; i--)
             right[i] = Math.Max(right[i + 1], arr[i]);
  
         //Calculate the accumulated water element by element
         //consider the amount of water on i'th bar, the
         //amount of water accumulated on this particular
         //bar will be equal to min(left[i], right[i]) - arr[i] .
         for ( int i = 0; i <n; i++)
             water += Math.Min(left[i], right[i]) - arr[i];
  
         return water;
     }
  
     //Driver method to test the above function
     public static void Main()
     {
  
         Console.WriteLine( "Maximum water that can be accumulated is " + findWater(arr.Length));
     }
}
  
//This code is contributed by vt_m.

的PHP

<?php
//PHP program to find maximum
//amount of water that can
//be trapped within given set of bars.
  
function findWater( $arr , $n )
{
      
     //left[i] contains height of
     //tallest bar to the
     //left of i'th bar including 
     //itself 
  
     //Right [i] contains height
     //of tallest bar to the right 
     //of ith bar including itself
     //$right[$n];
  
     //Initialize result
     $water = 0;
  
     //Fill left array
     $left [0] = $arr [0];
     for ( $i = 1; $i <$n ; $i ++)
     $left [ $i ] = max( $left [ $i - 1], $arr [ $i ]);
  
     //Fill right array
     $right [ $n - 1] = $arr [ $n - 1];
     for ( $i = $n - 2; $i>= 0; $i --)
     $right [ $i ] = max( $right [ $i + 1], $arr [ $i ]);
  
     //Calculate the accumulated
     //water element by element
     //consider the amount of 
     //water on i'th bar, the
     //amount of water accumulated
     //on this particular
     //bar will be equal to min(left[i], //right[i]) - arr[i] .
     for ( $i = 0; $i <$n ; $i ++)
     $water += min( $left [ $i ], $right [ $i ]) 
                              - $arr [ $i ];
  
     return $water ;
}
  
     //Driver program
     $arr = array (0, 1, 0, 2, 1, 0, 1, 3, 2, 1, 2, 1);
     $n = sizeof( $arr );
     echo "Maximum water that can be accumulated is " , findWater( $arr , $n );
      
//This code is contributed by ajit
?>

输出如下：

Maximum water that can be accumulated is 6

复杂度分析：
- 时间复杂度：上)。
  只需要遍历数组一次, 因此时间复杂度为O(n)。
- 空间复杂度：上)。
  需要两个额外的数组, 每个数组的大小为n。
以上解决方案的空间优化：代替维护两个大小为n的数组来存储每个元素的左右最大值, 而是维护两个变量以存储最大值直到该点。由于水被困在任何元素上=min(max_left, max_right)– arr [i]。首先计算从Alo和Ahi中捕获在较小元素上的水, 然后将指针移动到lo不交叉hi.
实现

C++

//C++ program to find maximum amount of water that can
//be trapped within given set of bars.
//Space Complexity : O(1)
  
#include <iostream>
using namespace std;
  
int findWater( int arr[], int n)
{
     //initialize output
     int result = 0;
  
     //maximum element on left and right
     int left_max = 0, right_max = 0;
  
     //indices to traverse the array
     int lo = 0, hi = n - 1;
  
     while (lo <= hi) {
         if (arr[lo] <arr[hi]) {
             if (arr[lo]> left_max)
                 //update max in left
                 left_max = arr[lo];
             else
                 //water on curr element = max - curr
                 result += left_max - arr[lo];
             lo++;
         }
         else {
             if (arr[hi]> right_max)
                 //update right maximum
                 right_max = arr[hi];
             else
                 result += right_max - arr[hi];
             hi--;
         }
     }
  
     return result;
}
  
int main()
{
     int arr[] = { 0, 1, 0, 2, 1, 0, 1, 3, 2, 1, 2, 1 };
     int n = sizeof (arr) /sizeof (arr[0]);
     cout <<"Maximum water that can be accumulated is "
          <<findWater(arr, n);
}
  
//This code is contributed by Aditi Sharma

Java

//JAVA Code For Trapping Rain Water
import java.util.*;
  
class GFG {
  
     static int findWater( int arr[], int n)
     {
         //initialize output
         int result = 0 ;
  
         //maximum element on left and right
         int left_max = 0 , right_max = 0 ;
  
         //indices to traverse the array
         int lo = 0 , hi = n - 1 ;
  
         while (lo <= hi) {
             if (arr[lo] <arr[hi]) {
                 if (arr[lo]> left_max)
  
                     //update max in left
                     left_max = arr[lo];
                 else
  
                     //water on curr element =
                     //max - curr
                     result += left_max - arr[lo];
                 lo++;
             }
             else {
                 if (arr[hi]> right_max)
  
                     //update right maximum
                     right_max = arr[hi];
  
                 else
                     result += right_max - arr[hi];
                 hi--;
             }
         }
  
         return result;
     }
  
     /* Driver program to test above function */
     public static void main(String[] args)
     {
         int arr[] = { 0 , 1 , 0 , 2 , 1 , 0 , 1 , 3 , 2 , 1 , 2 , 1 };
         int n = arr.length;
  
         System.out.println( "Maximum water that "
                            + "can be accumulated is "
                            + findWater(arr, n));
     }
}
//This code is contributed by Arnav Kr. Mandal.

Python3

# Python program to find
# maximum amount of water that can
# be trapped within given set of bars.
# Space Complexity : O(1)
  
def findWater(arr, n):
  
     # initialize output
     result = 0
       
     # maximum element on left and right
     left_max = 0
     right_max = 0
       
     # indices to traverse the array
     lo = 0
     hi = n - 1
       
     while (lo <= hi): 
      
         if (arr[lo] <arr[hi]):
          
             if (arr[lo]> left_max):
  
                 # update max in left
                 left_max = arr[lo]
             else :
  
                 # water on curr element = max - curr
                 result + = left_max - arr[lo]
             lo + = 1
          
         else :
          
             if (arr[hi]> right_max):
                 # update right maximum
                 right_max = arr[hi]
             else :
                 result + = right_max - arr[hi]
             hi - = 1
          
     return result
   
# Driver program
  
arr = [ 0 , 1 , 0 , 2 , 1 , 0 , 1 , 3 , 2 , 1 , 2 , 1 ]
n = len (arr)
  
print ( "Maximum water that can be accumulated is " , findWater(arr, n))
  
# This code is contributed
# by Anant Agarwal.

C#

//C# Code For Trapping Rain Water
using System;
  
class GFG {
  
     static int findWater( int [] arr, int n)
     {
         //initialize output
         int result = 0;
  
         //maximum element on left and right
         int left_max = 0, right_max = 0;
  
         //indices to traverse the array
         int lo = 0, hi = n - 1;
  
         while (lo <= hi) {
             if (arr[lo] <arr[hi]) {
                 if (arr[lo]> left_max)
  
                     //update max in left
                     left_max = arr[lo];
                 else
  
                     //water on curr element =
                     //max - curr
                     result += left_max - arr[lo];
                 lo++;
             }
             else {
                 if (arr[hi]> right_max)
  
                     //update right maximum
                     right_max = arr[hi];
  
                 else
                     result += right_max - arr[hi];
                 hi--;
             }
         }
  
         return result;
     }
  
     //Driver program
     public static void Main()
     {
         int [] arr = { 0, 1, 0, 2, 1, 0, 1, 3, 2, 1, 2, 1 };
         int result = Trap.findWater(arr, arr.length);
         System. out .print( " Total trapping water: " + result);
     }
}
  
//This code is contributed by vt_m.

的PHP

<?php
//PHP program to find maximum amount
//of water that can be trapped within 
//given set of bars.
  
//Method to find maximum amount
//of water that can be trapped within 
//given set of bars.
function findWater( $arr , $n )
{
      
     //initialize output
     $result = 0;
      
     //maximum element on 
     //left and right
     $left_max = 0; 
     $right_max = 0;
      
     //indices to traverse 
     //the array
     $lo = 0; $hi = $n - 1;
      
     while ( $lo <= $hi ) 
     {
         if ( $arr [ $lo ] <$arr [ $hi ])
         {
             if ( $arr [ $lo ]> $left_max )
              
                 //update max in left
                 $left_max = $arr [ $lo ];
              
             else
              
                 //water on curr 
                 //element = max - curr
                 $result += $left_max - $arr [ $lo ];
                 $lo ++;
         }
         else
         {
             if ( $arr [ $hi ]> $right_max )
              
                 //update right maximum
                 $right_max = $arr [ $hi ];
             else
                 $result += $right_max - $arr [ $hi ];
                 $hi --;
         }
     }
      
     return $result ;
}
  
     //Driver Code
     $arr = array (0, 1, 0, 2, 1, 0, 1, 3, 2, 1, 2, 1);
     $n = count ( $arr );
     echo "Maximum water that can be accumulated is " , findWater( $arr , $n ); 
  
//This code is contributed by anuj_67.
?>

输出如下:

Maximum water that can be accumulated is 6

复杂度分析：
- 时间复杂度：O(n)。
  只需遍历数组。
- 辅助空间：O(1)。
  由于不需要额外的空间。
感谢Gaurav Ahirwar和Aditi Sharma提供上述解决方案。

方法3：

这里显示了另一个有效的解决方案。

方法：这里的概念是, 如果右侧有较大的墙, 则可以保留与左侧较小的墙相同高度的水。如果右侧没有较大的墙, 则从左侧开始。现在左侧必须有一堵更大的墙。让我们举个例子, 如果高度为{…。, 3, 2, 1, 4, ....}, 那么这里3和4是边界, 高度2和1被淹没并且不能充当边界。因此, 在数组的其余部分中存在更高或相等长度的边界时, 在任何点或索引处都知道前一个边界就足够了。如果不是, 则向后遍历数组, 现在必须在左侧留一堵更大的墙。
算法：
- 从索引0循环到给定数组的末尾。
- 如果遇到大于或等于前一个墙的墙, 请在称为prev_index的变量中记录该墙的索引。
- 继续添加前一堵墙的高度减去当前高度(ith)墙壁上的可变水。
- 有一个临时变量, 该变量存储与水相同的值。
- 如果没有发现大于或等于前一个墙的墙, 则退出。
- 如果prev_index <输入数组的大小, 则从水中减去temp变量, 然后从输入数组的末尾循环到prev_index, 并找到大于或等于前一堵墙的墙(在这种情况下, 从后向查找最后一堵墙)。
实现

C++

//C++ implementation of the approach
#include<iostream>
using namespace std;
  
//Function to return the maximum
//water that can be stored
int maxWater( int arr[], int n)
{
     int size = n - 1;
  
     //Let the first element be stored as
     //previous, we shall loop from index 1
     int prev = arr[0];
  
     //To store previous wall's index
     int prev_index = 0;
     int water = 0;
  
     //To store the water until a larger wall
     //is found, if there are no larger walls
     //then delete temp value from water
     int temp = 0;
     for ( int i = 1; i <= size; i++)
     {
  
         //If the current wall is taller than
         //the previous wall then make current
         //wall as the previous wall and its
         //index as previous wall's index
         //for the subsequent loops
         if (arr[i]>= prev) 
         {
             prev = arr[i];
             prev_index = i;
  
             //Because larger or same 
             //height wall is found
             temp = 0;
         } 
         else
         {
              
             //Since current wall is shorter than
             //the previous, we subtract previous
             //wall's height from the current wall's
             //height and add it to the water
             water += prev - arr[i];
  
             //Store the same value in temp as well
             //If we dont find any larger wall then
             //we will subtract temp from water
             temp += prev - arr[i];
         }
     }
  
     //If the last wall was larger than or equal
     //to the previous wall then prev_index would
     //be equal to size of the array (last element)
     //If we didn't find a wall greater than or equal
     //to the previous wall from the left then
     //prev_index must be less than the index
     //of the last element
     if (prev_index <size) 
     {
  
         //Temp would've stored the water collected
         //from previous largest wall till the end
         //of array if no larger wall was found then
         //it has excess water and remove that
         //from water variable
         water -= temp;
  
         //We start from the end of the array, //so previous should be assigned to
         //the last element
         prev = arr[size];
  
         //Loop from the end of array up to the 
         //previous index which would contain
         //the largest wall from the left
         for ( int i = size; i>= prev_index; i--) 
         {
  
             //Right end wall will be definitely 
             //smaller than the 'previous index' wall
             if (arr[i]>= prev)
             {
                 prev = arr[i];
             } 
             else
             {
                 water += prev - arr[i];
             }
         }
     }
  
     //Return the maximum water
     return water;
}
  
//Driver Code
int main()
{
     int arr[] = { 0, 1, 0, 2, 1, 0, 1, 3, 2, 1, 2, 1 }; 
     int n = sizeof (arr) /sizeof (arr[0]);
  
     cout <<maxWater(arr, n);
     return 0;
}
  
//This code is contributed by Debidutta Rath

Java

//Java implementation of the approach
class GFG {
  
     //Function to return the maximum
     //water that can be stored
     public static int maxWater( int arr[], int n)
     {
         int size = n - 1 ;
  
         //Let the first element be stored as
         //previous, we shall loop from index 1
         int prev = arr[ 0 ];
  
         //To store previous wall's index
         int prev_index = 0 ;
         int water = 0 ;
  
         //To store the water until a larger wall
         //is found, if there are no larger walls
         //then delete temp value from water
         int temp = 0 ;
         for ( int i = 1 ; i <= size; i++) {
  
             //If the current wall is taller than
             //the previous wall then make current
             //wall as the previous wall and its
             //index as previous wall's index
             //for the subsequent loops
             if (arr[i]>= prev) {
                 prev = arr[i];
                 prev_index = i;
  
                 //Because larger or same height wall is found
                 temp = 0 ;
             }
             else {
  
                 //Since current wall is shorter than
                 //the previous, we subtract previous
                 //wall's height from the current wall's
                 //height and add it to the water
                 water += prev - arr[i];
  
                 //Store the same value in temp as well
                 //If we dont find any larger wall then
                 //we will subtract temp from water
                 temp += prev - arr[i];
             }
         }
  
         //If the last wall was larger than or equal
         //to the previous wall then prev_index would
         //be equal to size of the array (last element)
         //If we didn't find a wall greater than or equal
         //to the previous wall from the left then
         //prev_index must be less than the index
         //of the last element
         if (prev_index <size) {
  
             //Temp would've stored the water collected
             //from previous largest wall till the end
             //of array if no larger wall was found then
             //it has excess water and remove that
             //from 'water' var
             water -= temp;
  
             //We start from the end of the array, so previous
             //should be assigned to the last element
             prev = arr[size];
  
             //Loop from the end of array up to the 'previous index'
             //which would contain the "largest wall from the left"
             for ( int i = size; i>= prev_index; i--) {
  
                 //Right end wall will be definitely smaller
                 //than the 'previous index' wall
                 if (arr[i]>= prev) {
                     prev = arr[i];
                 }
                 else {
                     water += prev - arr[i];
                 }
             }
         }
  
         //Return the maximum water
         return water;
     }
  
     //Driver code
     public static void main(String[] args)
     {
         int arr[] = { 0 , 1 , 0 , 2 , 1 , 0 , 1 , 3 , 2 , 1 , 2 , 1 };
         int n = arr.length;
         System.out.print(maxWater(arr, n));
     }
}

Python3

# Pythpn3 implementation of the approach
  
# Function to return the maximum
# water that can be stored
def maxWater(arr, n):
     size = n - 1
  
     # Let the first element be stored as
     # previous, we shall loop from index 1
     prev = arr[ 0 ]
  
     # To store previous wall's index
     prev_index = 0
     water = 0
  
     # To store the water until a larger wall
     # is found, if there are no larger walls
     # then delete temp value from water
     temp = 0
     for i in range ( 1 , size + 1 ):
  
         # If the current wall is taller than
         # the previous wall then make current
         # wall as the previous wall and its
         # index as previous wall's index
         # for the subsequent loops
         if (arr[i]> = prev):
             prev = arr[i]
             prev_index = i
  
             # Because larger or same height wall is found
             temp = 0
         else :
  
             # Since current wall is shorter than
             # the previous, we subtract previous
             # wall's height from the current wall's
             # height and add it to the water
             water + = prev - arr[i]
  
             # Store the same value in temp as well
             # If we dont find any larger wall then
             # we will subtract temp from water
             temp + = prev - arr[i]
  
     # If the last wall was larger than or equal
     # to the previous wall then prev_index would
     # be equal to size of the array (last element)
     # If we didn't find a wall greater than or equal
     # to the previous wall from the left then
     # prev_index must be less than the index
     # of the last element
     if (prev_index <size):
  
         # Temp would've stored the water collected
         # from previous largest wall till the end
         # of array if no larger wall was found then
         # it has excess water and remove that
         # from 'water' var
         water - = temp
  
         # We start from the end of the array, so previous
         # should be assigned to the last element
         prev = arr[size]
  
         # Loop from the end of array up to the 'previous index'
         # which would contain the "largest wall from the left"
         for i in range (size, prev_index - 1 , - 1 ):
  
             # Right end wall will be definitely smaller
             # than the 'previous index' wall
             if (arr[i]> = prev):
                 prev = arr[i]
             else :
                 water + = prev - arr[i]
  
     # Return the maximum water
     return water
  
# Driver code
arr = [ 0 , 1 , 0 , 2 , 1 , 0 , 1 , 3 , 2 , 1 , 2 , 1 ]
n = len (arr)
print (maxWater(arr, n))
  
# This code is contributed by Mohit Kumar

输出如下：

复杂度分析：
- 时间复杂度：O(n)。
  由于只需要遍历该数组。
- 辅助空间：O(1)。
  由于不需要额外的空间。

方法4(使用栈)：

我们可以使用Stack来跟踪由较长的左右栏所限制的栏。只能使用Stacks进行一次迭代来完成此操作。

方法：

1.循环遍历bars数组的索引。

2.对于每个栏, 我们可以执行以下操作：

当栈不为空并且当前栏的高度大于栈的顶部栏时,
将顶栏索引存储在pop_height并从栈中弹出。
查找弹出的条的左条(当前顶部)与当前条之间的距离。
找到顶部栏和当前栏之间的最小高度。
可以捕获的最大水量是距离* min_height.
包括弹出条在内的被困水是(距离* min_height)–高度[pop_height].
将其添加到ans

3.最终答案将是ans.

C++

//C++ implementation of the approach
#include <bits/stdc++.h> 
using namespace std;
  
//Function to return the maximum
//water that can be stored
int maxWater( int height[], int n)
{
      
     //Stores the indices of the bars
     stack <int> st;
  
     //Stores the final result
     int ans = 0;
  
     //Loop through the each bar
     for ( int i = 0; i <n; i++)
     {
          
         //Remove bars from the stack
         //until the condition holds
         while ((!st.empty()) && 
                (height[st.top()] <height[i]))
         {
              
             //Store the height of the top
             //and pop it.
             int pop_height = height[st.top()];
             st.pop();
  
             //If the stack does not have any
             //bars or the the popped bar
             //has no left boundary
             if (st.empty())
                 break ;
  
             //Get the distance between the
             //left and right boundary of
             //popped bar
             int distance = i - st.top() - 1;
  
             //Calculate the min. height
             int min_height = min(height[st.top()], height[i]) -
                              pop_height;
  
             ans += distance * min_height;
         }
  
         //If the stack is either empty or
         //height of the current bar is less than
         //or equal to the top bar of stack
         st.push(i);
     }
     return ans;
}
  
//Driver code
int main() 
{
      
     int arr[] = { 0, 1, 0, 2, 1, 0, 1, 3, 2, 1, 2, 1 };
     int n = sizeof (arr) /sizeof (arr[0]);
      
     cout <<maxWater(arr, n);
  
     return 0;
}
  
//The code is contributed by Soumitri Chattopadhyay

Java

import java.util.*;
import java.io.*;
  
//Java implementation of the approach
class GFG {
  
     //Function to return the maximum
     //water that can be stored
     public static int maxWater( int [] height)
     {
         //Stores the indices of the bars
         Stack<Integer> stack = new Stack<>();
  
         //size of the array
         int n = height.length;
  
         //Stores the final result
         int ans = 0 ;
  
         //Loop through the each bar
         for ( int i = 0 ; i <n; i++) {
  
             //Remove bars from the stack
             //until the condition holds
             while ((!stack.isEmpty())
                    && (height[stack.peek()] <height[i])) {
  
                 //store the height of the top
                 //and pop it.
                 int pop_height = height[stack.peek()];
                 stack.pop();
  
                 //If the stack does not have any
                 //bars or the the popped bar
                 //has no left boundary
                 if (stack.isEmpty())
                     break ;
  
                 //Get the distance between the
                 //left and right boundary of
                 //popped bar
                 int distance = i - stack.peek() - 1 ;
  
                 //Calculate the min. height
                 int min_height
                     = Math.min(height[stack.peek()], height[i])
                       - pop_height;
  
                 ans += distance * min_height;
             }
  
             //If the stack is either empty or
             //height of the current bar is less than
             //or equal to the top bar of stack
             stack.push(i);
         }
  
         return ans;
     }
     //Driver code
     public static void main(String[] args)
     {
         int arr[] = { 0 , 1 , 0 , 2 , 1 , 0 , 1 , 3 , 2 , 1 , 2 , 1 };
         System.out.print(maxWater(arr));
     }
}

输出如下：

时间复杂度：O(n)

辅助空间：O(n)

如果发现任何不正确的地方, 或者想分享有关上述主题的更多信息, 请写评论。

本文概述

C++

Java

Python3

C++

Java

Python3

C#

的PHP

C++

Java

Python3

C#

的PHP

C++

Java

Python3

C++

Java

发表评论取消回复

登录 注册 找回密码

登录注册找回密码