Python探索相关性详细指南

本文旨在更好地了解一种非常重要的多元探索技术。

相关矩阵基本上是一个协方差矩阵。也被称为自协方差矩阵，分散矩阵，方差矩阵，或方差-协方差矩阵。它是一个矩阵，其中i-j位置定义了给定数据集的第i和第j个参数之间的相关性。

当数据点大致呈直线趋势时，这些变量就称为近似线性关系。在某些情况下，数据点接近于一条直线，但更多情况下，在直线趋势周围的点有相当大的可变性。一种称为相关性的概括性度量方法描述了线性关联的强度。相关性概括了两个定量变量之间线性(直线)关联的强度和方向。用r表示，它的值在-1到+1之间。r为正表示正关联，r为负表示负关联。

r越接近1，数据点越接近直线，线性关联越强。r越接近0，线性关联就越弱。

要获取到House_price数据的链接, 请单击这里：https://drive.google.com/open?id=1ac0_iyVeT4QlsHcMII9cIGzAQDtKClp3

加载库

import numpy as np
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
from scipy.stats import norm

加载数据中

data = pd.read_csv( "House Price.csv" )
data.shape

输出如下：

(1460, 81)

"销售价格"说明

data[ 'SalePrice' ].describe()

输出如下：

count      1460.000000
mean     180921.195890
std       79442.502883
min       34900.000000
25%      129975.000000
50%      163000.000000
75%      214000.000000
max      755000.000000
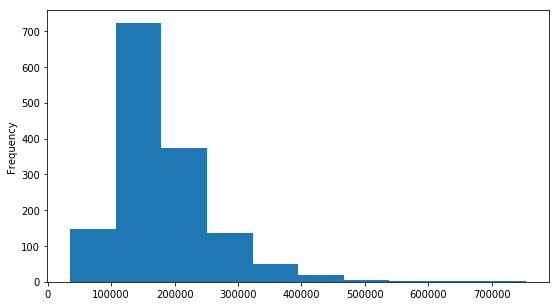
Name: SalePrice, dtype: float64

直方图

plt.figure(figsize = ( 9 , 5 ))
data[ 'SalePrice' ].plot(kind = "hist" )

输出如下：

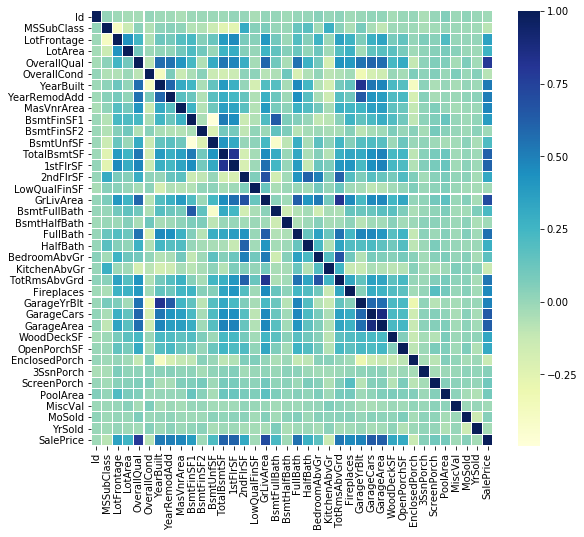
代码1：相关矩阵

corrmat = data.corr()
  
f, ax = plt.subplots(figsize = ( 9 , 8 ))
sns.heatmap(corrmat, ax = ax, cmap = "YlGnBu" , linewidths = 0.1 )

输出如下：

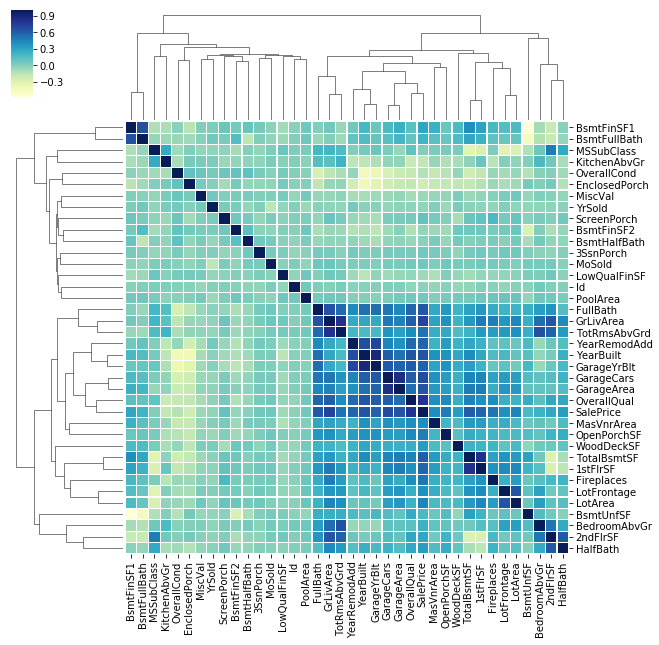
代码2：网格相关矩阵

corrmat = data.corr()
  
cg = sns.clustermap(corrmat, cmap = "YlGnBu" , linewidths = 0.1 );
plt.setp(cg.ax_heatmap.yaxis.get_majorticklabels(), rotation = 0 )
  
cg

输出如下：

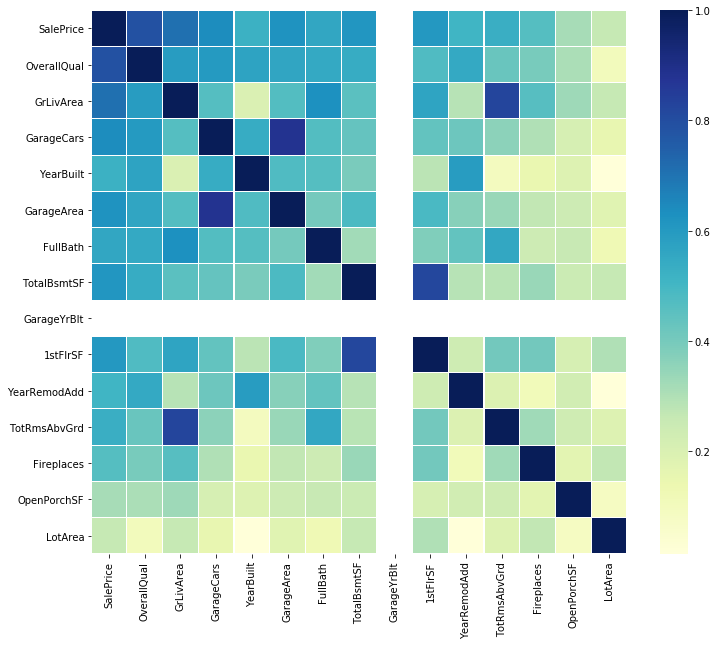
代码3：销售价格的相关性

# saleprice correlation matrix
# k : number of variables for heatmap
k = 15 
  
cols = corrmat.nlargest(k, 'SalePrice' )[ 'SalePrice' ].index
  
cm = np.corrcoef(data[cols].values.T)
f, ax = plt.subplots(figsize = ( 12 , 10 ))
  
sns.heatmap(cm, ax = ax, cmap = "YlGnBu" , linewidths = 0.1 , yticklabels = cols.values, xticklabels = cols.values)

输出如下：

首先, 你的面试准备可通过以下方式增强你的数据结构概念：Python DS课程。

---