什么是相关性测试?
两个变量之间的关联强度称为相关性测试。
例如, 如果我们想知道父亲和儿子的身高之间是否存在关系, 可以计算相关系数来回答这个问题。
有关关联的更多信息, 请参阅这个。
相关分析方法:
- 参数相关:它测量两个变量(x和y)之间的线性相关性, 这被称为参数相关性测试, 因为它取决于数据的分布。
- 非参数相关:肯德尔(tau)和矛兵(Rho)是基于等级的相关系数, 称为非参数相关。
注意:最常用的方法是参数相关方法。
皮尔逊相关公式:
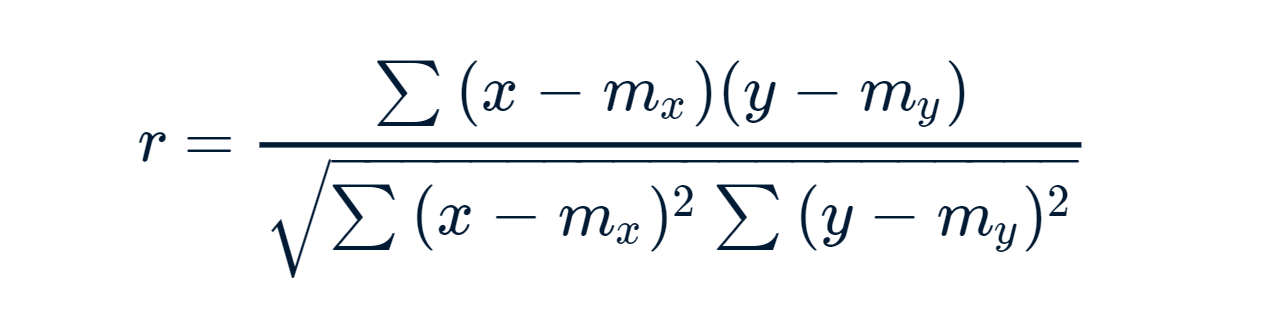
x和y是长度为n m的两个向量, x和m, y分别对应于x和y的均值。
注意:
- r取值介于-1(负相关)和1(正相关)之间。
- r = 0表示没有相关性。
- 不能应用于序数变量。
- 样本大小应适中(20-30), 以进行良好的估算。
- 离群值可能导致误导值, 这意味着对离群值的鲁棒性不足。
在Python中计算Pearson相关性–
pearsonr()
功能可以使用。
Python函数
语法:pearsonr(x, y)参数:x, y:相同长度的数值向量
数据:下载csv文件这里。
代码:找到梨子相关性的Python代码
# Import those libraries
import pandas as pd
from scipy.stats import pearsonr
# Import your data into Python
df = pd.read_csv( "Auto.csv" )
# Convert dataframe into series
list1 = df[ 'weight' ]
list2 = df[ 'mpg' ]
# Apply the pearsonr()
corr, _ = pearsonr(list1, list2)
print ( 'Pearsons correlation: %.3f' % corr)
# This code is contributed by Amiya Rout输出如下:
Pearson correlation is: -0.878用于Anscombe数据的Pearson相关:
Anscombe的数据(也称为Anscombe的四重奏)由四个数据集组成, 这些数据集具有几乎相同的简单统计属性, 但在绘制时却显得非常不同。每个数据集由十一个(x, y)点组成。它们由统计学家Francis Anscombe于1973年建造, 旨在证明在分析数据之前对数据进行图形绘制的重要性以及离群值对统计属性的影响。
这里给出了这4组11个数据点。请下载csv文件
这里。
当我们绘制这些点时, 它看起来像这样。我在这里考虑3组11个数据点。
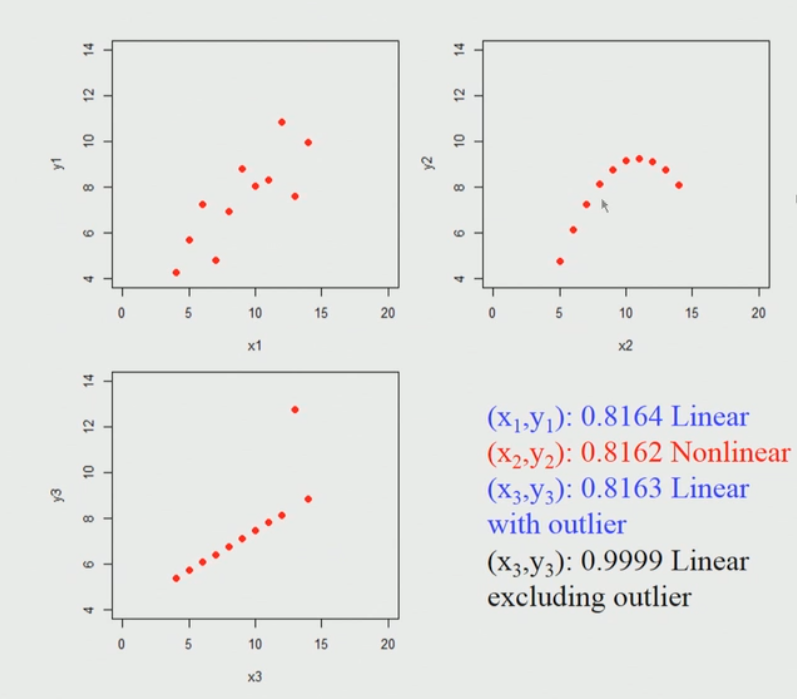
上图的简要说明:
因此, 如果我们对这些数据集的每个应用皮尔逊相关系数, 我们发现它几乎相同, 那么实际上是应用到第一个数据集(左上)还是第二个数据集(右上)还是第三个数据集都没关系数据集(左下)。
因此, 似乎表明, 如果我们应用Pearson的相关性, 并且在第一个数据集(左上)中发现高相关系数接近一个。关键是在这里我们不能立即得出结论, 如果Pearson相关系数将很高, 则它们之间存在线性关系, 例如在第二个数据集(右上)中, 这是非线性关系, 并且仍然带来很高的价值。
首先, 你的面试准备可通过以下方式增强你的数据结构概念:Python DS课程。

