聚类分析或简单地说, 聚类基本上是一种无监督的学习方法, 可以将数据点分为多个特定的批次或组, 这样, 同一组中的数据点具有相似的属性, 而不同组中的数据点在某种意义上具有不同的属性。它包括基于不同演变的许多不同方法。
例如。 K均值(点之间的距离), 亲和力传播(图形距离), 均值偏移(点之间的距离), DBSCAN(最近点之间的距离), 高斯混合(马哈拉诺比斯到中心的距离), 谱聚类(图形距离)等。
从根本上讲, 所有聚类方法都使用相同的方法, 即首先我们计算相似度, 然后使用它将数据点聚类为组或批次。在这里, 我们将专注于基于密度的含噪声应用程序空间聚类(DBSCAN)群集方法。
簇是数据空间中的密集区域, 由点密度较低的区域分隔。的
DBSCAN算法
基于"集群"和"噪声"的直观概念。关键思想是, 对于群集的每个点, 给定半径的邻域必须至少包含最少数量的点。
为什么选择DBSCAN?
分区方法(K均值, PAM聚类)和层次聚类用于查找球形聚类或凸形聚类。换句话说, 它们仅适用于紧凑且间隔良好的群集。此外, 它们还受到数据中存在噪声和异常值的严重影响。
现实生活中的数据可能包含违规行为, 例如–
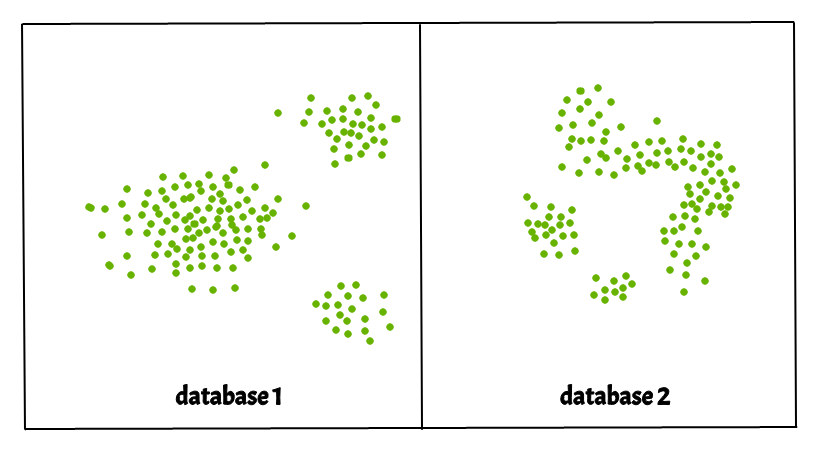
i)簇可以是任意形状, 如下图所示。
ii)数据可能包含噪音。

下图显示了一个包含非凸簇和离群值/噪声的数据集。给定这样的数据, k-均值算法很难识别具有任意形状的这些聚类。
DBSCAN算法需要两个参数–
eps:它定义了数据点周围的邻域, 即, 如果两个点之间的距离小于或等于" eps", 则将它们视为邻居。如果eps值选择得太小, 则大部分数据将被视为离群值。如果选择非常大, 则群集将合并, 并且大多数数据点将位于同一群集中。查找eps值的一种方法是基于k距离图。
最小点数
:eps半径内的最小邻居(数据点)数。数据集越大, 必须选择更大的MinPts值。通常, 最小MinPts可以从数据集中的维数D得出, 如MinPts> = D + 1。 MinPts的最小值必须至少选择3。
在此算法中, 我们有3种类型的数据点。核心点:如果点在eps内的点数超过MinPts, 则该点就是核心点。边界点:在eps内少于MinPts的点, 但它在核心点附近。噪点或异常值:不是核心点或边界点的点。
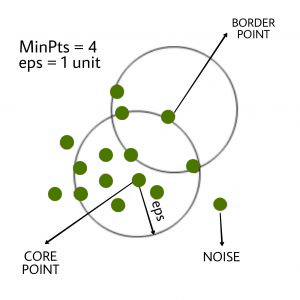
DBSCAN算法可以在以下步骤中抽象化–
- 找到eps内的所有相邻点, 并确定核心点或与MinPts相邻的点进行访问。
- 对于尚未分配给集群的每个核心点, 请创建一个新集群。
- 递归查找其所有密度连接点, 并将其分配给与核心点相同的群集。
一个点一种和b如果存在一点, 就说是密度连接C在它的邻居和两个点中都有足够数量的点一种和b在eps距离。这是一个链接过程。因此, 如果b是的邻居C, C是的邻居d, d是的邻居Ë, 而后者又是一种暗示b是的邻居一种. - 遍历数据集中剩余的未访问点。不属于任何群集的那些点是噪声。
下面是伪代码中的DBSCAN聚类算法:
DBSCAN(dataset, eps, MinPts){
# cluster index
C = 1
for each unvisited point p in dataset {
mark p as visited
# find neighbors
Neighbors N = find the neighboring points of p
if |N|>=MinPts:
N = N U N'
if p' is not a member of any cluster:
add p' to cluster C
}以上算法在Python中的实现:
在这里, 我们将使用Python库斯克莱恩计算DBSCAN。我们还将使用matplotlib.pyplot用于可视化集群的库。
可以找到使用的数据集这里.
import numpy as np
from sklearn.cluster import DBSCAN
from sklearn import metrics
from sklearn.datasets.samples_generator import make_blobs
from sklearn.preprocessing import StandardScaler
from sklearn import datasets
# Load data in X
db = DBSCAN(eps = 0.3 , min_samples = 10 ).fit(X)
core_samples_mask = np.zeros_like(db.labels_, dtype = bool )
core_samples_mask[db.core_sample_indices_] = True
labels = db.labels_
# Number of clusters in labels, ignoring noise if present.
n_clusters_ = len ( set (labels)) - ( 1 if - 1 in labels else 0 )
print (labels)
# Plot result
import matplotlib.pyplot as plt
# Black removed and is used for noise instead.
unique_labels = set (labels)
colors = [ 'y' , 'b' , 'g' , 'r' ]
print (colors)
for k, col in zip (unique_labels, colors):
if k = = - 1 :
# Black used for noise.
col = 'k'
class_member_mask = (labels = = k)
xy = X[class_member_mask & core_samples_mask]
plt.plot(xy[:, 0 ], xy[:, 1 ], 'o' , markerfacecolor = col, markeredgecolor = 'k' , markersize = 6 )
xy = X[class_member_mask & ~core_samples_mask]
plt.plot(xy[:, 0 ], xy[:, 1 ], 'o' , markerfacecolor = col, markeredgecolor = 'k' , markersize = 6 )
plt.title( 'number of clusters: %d' % n_clusters_)
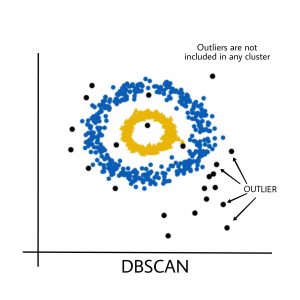
plt.show()输出如下:
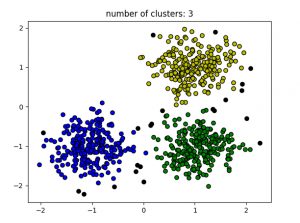
黑点代表异常值。通过更改eps和MinPts,我们可以更改集群配置。
现在应该提出的问题是,为什么我们要使用DBSCAN,而K-Means是聚类分析中广泛使用的方法?
K-MEANS的缺点:
K均值仅形成球形簇。当数据不是球形时(即在所有方向上都具有相同的方差), 该算法将失败。
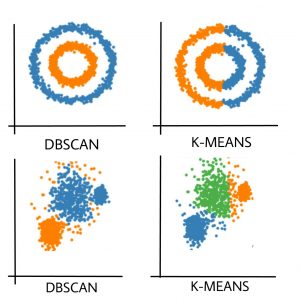
K-Means算法对异常敏感。离群值可以在很大程度上扭曲K均值中的聚类。
K-Means算法需要先指定优先级等的簇数。
DBSCAN算法基本上克服了K-Means算法的上述缺点。DBSCAN算法通过基于距离测量将彼此接近的数据点分组来识别密集区域。
参考文献:
https://en.wikipedia.org/wiki/DBSCAN
https://scikit-learn.org/stable/auto_examples/cluster/plot_dbscan.html
首先, 你的面试准备可通过以下方式增强你的数据结构概念:Python DS课程。

