本文概述
我们建议阅读以下两篇文章, 作为这篇文章Dijkstra算法的先决条件。
1. 贪婪算法|S7(Dijkstra的最短路径算法)
2. 图及其表示
我们已经讨论过Dijkstra算法及其图形邻接矩阵表示的实现。矩阵表示的时间复杂度为O(V ^ 2)。在这篇文章中, 讨论了用于邻接表表示的O(ELogV)算法。
在之前的文章中讨论过,在Dijkstra算法中,维护了两个集合,一个集合包含已经包含在SPT(最短路径树)中的顶点列表,另一个集合包含还没有包含的顶点。利用邻接表表示,使用BFS可以在O(V+E)时间内遍历图的所有顶点。其思想是使用BFS遍历graph的所有顶点,并使用最小堆存储SPT中未包含的顶点(或最短距离尚未最终确定的顶点)。最小堆被用作优先队列,以从尚未包含的顶点集获得最小距离顶点。提取- Min和减小-key值等操作的时间复杂度为O(LogV)。
以下是详细步骤。
1)创建大小为V的最小堆, 其中V是给定图中的顶点数。最小堆的每个节点都包含顶点数和顶点的距离值。
2)以源顶点为根初始化Min Heap(分配给源顶点的距离值为0)。分配给所有其他顶点的距离值为INF(无限)。
3)当Min Heap不为空时, 请执行以下操作
…..a)从最小堆中提取具有最小距离值节点的顶点。令提取的顶点为u。
…..b)对于u的每个相邻顶点v, 检查v是否在Min Heap中。如果v在"最小堆"中, 并且距离值大于u-v的权重加上u的距离值, 则更新v的距离值。
让我们用下面的例子来理解。让给定的源顶点为0
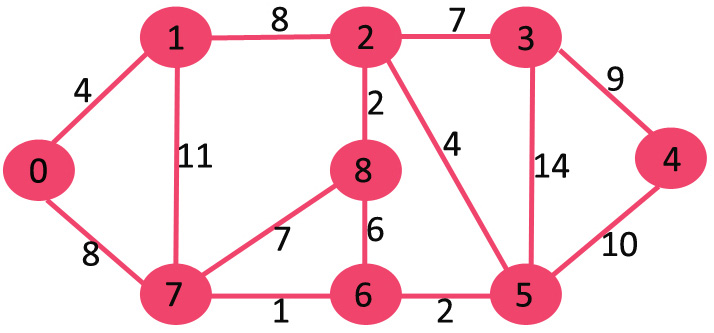
最初, 对于所有其他顶点, 源顶点的距离值为0, INF为无穷大。因此, 从"最小堆"中提取源顶点, 并更新与0(1和7)相邻的顶点的距离值。最小堆包含除顶点0以外的所有顶点。
绿色的顶点是已确定最小距离且不在最小堆中的顶点
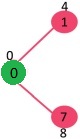
由于顶点1的距离值在最小堆中的所有节点中最小, 因此从最小堆中提取顶点, 并更新与1相邻的顶点的距离值(如果顶点在最小堆中并且到1的距离小于以前的距离)。最小堆包含除顶点0和1之外的所有顶点。
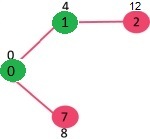
从最小堆中选取最小距离值的顶点。选择了顶点7。因此, 最小堆现在包含除0、1和7以外的所有顶点。更新相邻顶点7的距离值。顶点6和8的距离值变得有限(分别为15和9)。
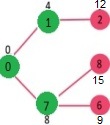
选择与最小堆的距离最小的顶点。选择了顶点6。因此, 最小堆现在包含除0、1、7和6以外的所有顶点。更新相邻顶点6的距离值。更新顶点5和8的距离值。
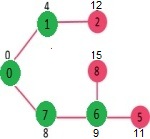
重复上述步骤, 直到最小堆不为空为止。最后, 我们得到以下最短路径树。
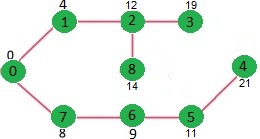
Dijkstra的最短路径算法,使用邻接表表示的贪婪算法实现代码如下:
C ++
//C /C++ program for Dijkstra's
//shortest path algorithm for adjacency
//list representation of graph
#include <stdio.h>
#include <stdlib.h>
#include <limits.h>
//A structure to represent a
//node in adjacency list
struct AdjListNode
{
int dest;
int weight;
struct AdjListNode* next;
};
//A structure to represent
//an adjacency list
struct AdjList
{
//Pointer to head node of list
struct AdjListNode *head;
};
//A structure to represent a graph.
//A graph is an array of adjacency lists.
//Size of array will be V (number of
//vertices in graph)
struct Graph
{
int V;
struct AdjList* array;
};
//A utility function to create
//a new adjacency list node
struct AdjListNode* newAdjListNode(
int dest, int weight)
{
struct AdjListNode* newNode =
( struct AdjListNode*)
malloc ( sizeof ( struct AdjListNode));
newNode->dest = dest;
newNode->weight = weight;
newNode->next = NULL;
return newNode;
}
//A utility function that creates
//a graph of V vertices
struct Graph* createGraph( int V)
{
struct Graph* graph = ( struct Graph*)
malloc ( sizeof ( struct Graph));
graph->V = V;
//Create an array of adjacency lists.
//Size of array will be V
graph->array = ( struct AdjList*)
malloc (V * sizeof ( struct AdjList));
//Initialize each adjacency list
//as empty by making head as NULL
for ( int i = 0; i <V; ++i)
graph->array[i].head = NULL;
return graph;
}
//Adds an edge to an undirected graph
void addEdge( struct Graph* graph, int src, int dest, int weight)
{
//Add an edge from src to dest.
//A new node is added to the adjacency
//list of src. The node is
//added at the beginning
struct AdjListNode* newNode =
newAdjListNode(dest, weight);
newNode->next = graph->array[src].head;
graph->array[src].head = newNode;
//Since graph is undirected, //add an edge from dest to src also
newNode = newAdjListNode(src, weight);
newNode->next = graph->array[dest].head;
graph->array[dest].head = newNode;
}
//Structure to represent a min heap node
struct MinHeapNode
{
int v;
int dist;
};
//Structure to represent a min heap
struct MinHeap
{
//Number of heap nodes present currently
int size;
//Capacity of min heap
int capacity;
//This is needed for decreaseKey()
int *pos;
struct MinHeapNode **array;
};
//A utility function to create a
//new Min Heap Node
struct MinHeapNode* newMinHeapNode( int v, int dist)
{
struct MinHeapNode* minHeapNode =
( struct MinHeapNode*)
malloc ( sizeof ( struct MinHeapNode));
minHeapNode->v = v;
minHeapNode->dist = dist;
return minHeapNode;
}
//A utility function to create a Min Heap
struct MinHeap* createMinHeap( int capacity)
{
struct MinHeap* minHeap =
( struct MinHeap*)
malloc ( sizeof ( struct MinHeap));
minHeap->pos = ( int *) malloc (
capacity * sizeof ( int ));
minHeap->size = 0;
minHeap->capacity = capacity;
minHeap->array =
( struct MinHeapNode**)
malloc (capacity *
sizeof ( struct MinHeapNode*));
return minHeap;
}
//A utility function to swap two
//nodes of min heap.
//Needed for min heapify
void swapMinHeapNode( struct MinHeapNode** a, struct MinHeapNode** b)
{
struct MinHeapNode* t = *a;
*a = *b;
*b = t;
}
//A standard function to
//heapify at given idx
//This function also updates
//position of nodes when they are swapped.
//Position is needed for decreaseKey()
void minHeapify( struct MinHeap* minHeap, int idx)
{
int smallest, left, right;
smallest = idx;
left = 2 * idx + 1;
right = 2 * idx + 2;
if (left <minHeap->size &&
minHeap->array[left]->dist <
minHeap->array[smallest]->dist )
smallest = left;
if (right <minHeap->size &&
minHeap->array[right]->dist <
minHeap->array[smallest]->dist )
smallest = right;
if (smallest != idx)
{
//The nodes to be swapped in min heap
MinHeapNode *smallestNode =
minHeap->array[smallest];
MinHeapNode *idxNode =
minHeap->array[idx];
//Swap positions
minHeap->pos[smallestNode->v] = idx;
minHeap->pos[idxNode->v] = smallest;
//Swap nodes
swapMinHeapNode(&minHeap->array[smallest], &minHeap->array[idx]);
minHeapify(minHeap, smallest);
}
}
//A utility function to check if
//the given minHeap is ampty or not
int isEmpty( struct MinHeap* minHeap)
{
return minHeap->size == 0;
}
//Standard function to extract
//minimum node from heap
struct MinHeapNode* extractMin( struct MinHeap*
minHeap)
{
if (isEmpty(minHeap))
return NULL;
//Store the root node
struct MinHeapNode* root =
minHeap->array[0];
//Replace root node with last node
struct MinHeapNode* lastNode =
minHeap->array[minHeap->size - 1];
minHeap->array[0] = lastNode;
//Update position of last node
minHeap->pos[root->v] = minHeap->size-1;
minHeap->pos[lastNode->v] = 0;
//Reduce heap size and heapify root
--minHeap->size;
minHeapify(minHeap, 0);
return root;
}
//Function to decreasy dist value
//of a given vertex v. This function
//uses pos[] of min heap to get the
//current index of node in min heap
void decreaseKey( struct MinHeap* minHeap, int v, int dist)
{
//Get the index of v in heap array
int i = minHeap->pos[v];
//Get the node and update its dist value
minHeap->array[i]->dist = dist;
//Travel up while the complete
//tree is not hepified.
//This is a O(Logn) loop
while (i && minHeap->array[i]->dist <
minHeap->array[(i - 1) /2]->dist)
{
//Swap this node with its parent
minHeap->pos[minHeap->array[i]->v] =
(i-1)/2;
minHeap->pos[minHeap->array[
(i-1)/2]->v] = i;
swapMinHeapNode(&minHeap->array[i], &minHeap->array[(i - 1) /2]);
//move to parent index
i = (i - 1) /2;
}
}
//A utility function to check if a given vertex
//'v' is in min heap or not
bool isInMinHeap( struct MinHeap *minHeap, int v)
{
if (minHeap->pos[v] <minHeap->size)
return true ;
return false ;
}
//A utility function used to print the solution
void printArr( int dist[], int n)
{
printf ( "Vertex Distance from Source\n" );
for ( int i = 0; i <n; ++i)
printf ( "%d \t\t %d\n" , i, dist[i]);
}
//The main function that calulates
//distances of shortest paths from src to all
//vertices. It is a O(ELogV) function
void dijkstra( struct Graph* graph, int src)
{
//Get the number of vertices in graph
int V = graph->V;
//dist values used to pick
//minimum weight edge in cut
int dist[V];
//minHeap represents set E
struct MinHeap* minHeap = createMinHeap(V);
//Initialize min heap with all
//vertices. dist value of all vertices
for ( int v = 0; v <V; ++v)
{
dist[v] = INT_MAX;
minHeap->array[v] = newMinHeapNode(v, dist[v]);
minHeap->pos[v] = v;
}
//Make dist value of src vertex
//as 0 so that it is extracted first
minHeap->array[src] =
newMinHeapNode(src, dist[src]);
minHeap->pos[src] = src;
dist[src] = 0;
decreaseKey(minHeap, src, dist[src]);
//Initially size of min heap is equal to V
minHeap->size = V;
//In the followin loop, //min heap contains all nodes
//whose shortest distance
//is not yet finalized.
while (!isEmpty(minHeap))
{
//Extract the vertex with
//minimum distance value
struct MinHeapNode* minHeapNode =
extractMin(minHeap);
//Store the extracted vertex number
int u = minHeapNode->v;
//Traverse through all adjacent
//vertices of u (the extracted
//vertex) and update
//their distance values
struct AdjListNode* pCrawl =
graph->array[u].head;
while (pCrawl != NULL)
{
int v = pCrawl->dest;
//If shortest distance to v is
//not finalized yet, and distance to v
//through u is less than its
//previously calculated distance
if (isInMinHeap(minHeap, v) &&
dist[u] != INT_MAX &&
pCrawl->weight + dist[u] <dist[v])
{
dist[v] = dist[u] + pCrawl->weight;
//update distance
//value in min heap also
decreaseKey(minHeap, v, dist[v]);
}
pCrawl = pCrawl->next;
}
}
//print the calculated shortest distances
printArr(dist, V);
}
//Driver program to test above functions
int main()
{
//create the graph given in above fugure
int V = 9;
struct Graph* graph = createGraph(V);
addEdge(graph, 0, 1, 4);
addEdge(graph, 0, 7, 8);
addEdge(graph, 1, 2, 8);
addEdge(graph, 1, 7, 11);
addEdge(graph, 2, 3, 7);
addEdge(graph, 2, 8, 2);
addEdge(graph, 2, 5, 4);
addEdge(graph, 3, 4, 9);
addEdge(graph, 3, 5, 14);
addEdge(graph, 4, 5, 10);
addEdge(graph, 5, 6, 2);
addEdge(graph, 6, 7, 1);
addEdge(graph, 6, 8, 6);
addEdge(graph, 7, 8, 7);
dijkstra(graph, 0);
return 0;
}python
# A Python program for Dijkstra's shortest
# path algorithm for adjacency
# list representation of graph
from collections import defaultdict
import sys
class Heap():
def __init__( self ):
self .array = []
self .size = 0
self .pos = []
def newMinHeapNode( self , v, dist):
minHeapNode = [v, dist]
return minHeapNode
# A utility function to swap two nodes
# of min heap. Needed for min heapify
def swapMinHeapNode( self , a, b):
t = self .array[a]
self .array[a] = self .array[b]
self .array[b] = t
# A standard function to heapify at given idx
# This function also updates position of nodes
# when they are swapped.Position is needed
# for decreaseKey()
def minHeapify( self , idx):
smallest = idx
left = 2 * idx + 1
right = 2 * idx + 2
if left <self .size and
self .array[left][ 1 ] \
<self .array[smallest][ 1 ]:
smallest = left
if right <self .size and
self .array[right][ 1 ]\
<self .array[smallest][ 1 ]:
smallest = right
# The nodes to be swapped in min
# heap if idx is not smallest
if smallest ! = idx:
# Swap positions
self .pos[ self .array[smallest][ 0 ]]
= idx
self .pos[ self .array[idx][ 0 ]] =
smallest
# Swap nodes
self .swapMinHeapNode(smallest, idx)
self .minHeapify(smallest)
# Standard function to extract minimum
# node from heap
def extractMin( self ):
# Return NULL wif heap is empty
if self .isEmpty() = = True :
return
# Store the root node
root = self .array[ 0 ]
# Replace root node with last node
lastNode = self .array[ self .size - 1 ]
self .array[ 0 ] = lastNode
# Update position of last node
self .pos[lastNode[ 0 ]] = 0
self .pos[root[ 0 ]] = self .size - 1
# Reduce heap size and heapify root
self .size - = 1
self .minHeapify( 0 )
return root
def isEmpty( self ):
return True if self .size = = 0 else False
def decreaseKey( self , v, dist):
# Get the index of v in heap array
i = self .pos[v]
# Get the node and update its dist value
self .array[i][ 1 ] = dist
# Travel up while the complete tree is
# not hepified. This is a O(Logn) loop
while i> 0 and self .array[i][ 1 ] <
self .array[(i - 1 ) /2 ][ 1 ]:
# Swap this node with its parent
self .pos[ self .array[i][ 0 ] ] = (i - 1 ) /2
self .pos[ self .array[(i - 1 ) /2 ][ 0 ] ] = i
self .swapMinHeapNode(i, (i - 1 ) /2 )
# move to parent index
i = (i - 1 ) /2 ;
# A utility function to check if a given
# vertex 'v' is in min heap or not
def isInMinHeap( self , v):
if self .pos[v] <self .size:
return True
return False
def printArr(dist, n):
print "Vertex\tDistance from source"
for i in range (n):
print "%d\t\t%d" % (i, dist[i])
class Graph():
def __init__( self , V):
self .V = V
self .graph = defaultdict( list )
# Adds an edge to an undirected graph
def addEdge( self , src, dest, weight):
# Add an edge from src to dest. A new node
# is added to the adjacency list of src. The
# node is added at the beginning. The first
# element of the node has the destination
# and the second elements has the weight
newNode = [dest, weight]
self .graph[src].insert( 0 , newNode)
# Since graph is undirected, add an edge
# from dest to src also
newNode = [src, weight]
self .graph[dest].insert( 0 , newNode)
# The main function that calulates distances
# of shortest paths from src to all vertices.
# It is a O(ELogV) function
def dijkstra( self , src):
V = self .V # Get the number of vertices in graph
dist = [] # dist values used to pick minimum
# weight edge in cut
# minHeap represents set E
minHeap = Heap()
# Initialize min heap with all vertices.
# dist value of all vertices
for v in range (V):
dist.append(sys.maxint)
minHeap.array.append( minHeap.
newMinHeapNode(v, dist[v]))
minHeap.pos.append(v)
# Make dist value of src vertex as 0 so
# that it is extracted first
minHeap.pos[src] = src
dist[src] = 0
minHeap.decreaseKey(src, dist[src])
# Initially size of min heap is equal to V
minHeap.size = V;
# In the following loop, # min heap contains all nodes
# whose shortest distance is not yet finalized.
while minHeap.isEmpty() = = False :
# Extract the vertex
# with minimum distance value
newHeapNode = minHeap.extractMin()
u = newHeapNode[ 0 ]
# Traverse through all adjacent vertices of
# u (the extracted vertex) and update their
# distance values
for pCrawl in self .graph[u]:
v = pCrawl[ 0 ]
# If shortest distance to v is not finalized
# yet, and distance to v through u is less
# than its previously calculated distance
if minHeap.isInMinHeap(v) and
dist[u] ! = sys.maxint and \
pCrawl[ 1 ] + dist[u] <dist[v]:
dist[v] = pCrawl[ 1 ] + dist[u]
# update distance value
# in min heap also
minHeap.decreaseKey(v, dist[v])
printArr(dist, V)
# Driver program to test the above functions
graph = Graph( 9 )
graph.addEdge( 0 , 1 , 4 )
graph.addEdge( 0 , 7 , 8 )
graph.addEdge( 1 , 2 , 8 )
graph.addEdge( 1 , 7 , 11 )
graph.addEdge( 2 , 3 , 7 )
graph.addEdge( 2 , 8 , 2 )
graph.addEdge( 2 , 5 , 4 )
graph.addEdge( 3 , 4 , 9 )
graph.addEdge( 3 , 5 , 14 )
graph.addEdge( 4 , 5 , 10 )
graph.addEdge( 5 , 6 , 2 )
graph.addEdge( 6 , 7 , 1 )
graph.addEdge( 6 , 8 , 6 )
graph.addEdge( 7 , 8 , 7 )
graph.dijkstra( 0 )
# This code is contributed by Divyanshu Mehta输出如下:
Vertex Distance from Source
0 0
1 4
2 12
3 19
4 21
5 11
6 9
7 8
8 14Dijkstra算法时间复杂度:上面的代码/算法的时间复杂度看起来是O(V ^ 2), 因为有两个嵌套的while循环。如果仔细观察, 可以观察到内部循环中的语句执行了O(V + E)次(类似于BFS)。内部循环具有reduceKey()操作, 该操作需要O(LogV)时间。因此, 总体时间复杂度为O(E + V)* O(LogV), 即O((E + V)* LogV)= O(ELogV)
请注意, 以上代码将Binary Heap用于Priority Queue实现。使用斐波那契堆可以将时间复杂度降低到O(E + VLogV)。原因是, 斐波那契堆需要O(1)时间来进行减键操作, 而二进制堆需要O(Logn)时间。该算法是一个贪婪算法,使用优先队列是该类型算法的典型形式。
Dijkstra的最短路径算法笔记:
- 该代码计算最短距离, 但不计算路径信息。我们可以创建一个父数组, 在距离更新时更新父数组(例如总理的实施), 并使用它显示从源到不同顶点的最短路径。
- 该代码用于无向图, 相同的dijekstra函数也可用于有向图。
- 该代码查找从源到所有顶点的最短距离。如果我们在最短的距离只关心从源到单个目标, 我们可以break for循环时所拾取最小距离顶点等于目标(算法的步骤3.A)。
- Dijkstra算法不适用于负边缘为负的图表。对于负负边的图形, Bellman–Ford算法可以使用, 我们将在单独的文章中进行讨论。
Dijkstra最短路径算法中的打印路径
Dijkstra使用STL中的集合的最短路径算法
参考文献:
Clifford Stein, Thomas H.Cormen, Charles E.Leiserson, Ronald L.
Sanjoy Dasgupta, Christos Papadimitriou, Umesh Vazirani的算法
如果发现任何不正确的地方, 或者想分享有关上述主题的更多信息, 请写评论。

![从字法上最小长度N的排列,使得对于正好为K个索引,a[i] a[i]+1](https://www.lsbin.com/wp-content/themes/begin%20lts/img/loading.png)