填充矩阵以使所有行和所有列的乘积等于1的方式

2021年4月4日18:26:49 发表评论 941 次浏览

本文概述

给我们三个值

ñ

,

米

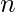
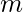
和

ķ

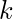
其中

ñ

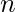
是矩阵中的行数,

米

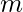
是矩阵中的列数, 并且

ķ

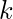
是只能具有两个值-1和1的数字。我们的目的是找到填充矩阵的方式的数目。

n \次m

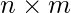
这样每一行每一列中所有元素的乘积等于

ķ

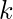
。由于方法的数量可能很大, 我们将输出

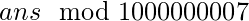
ans \ mod {1000000007}

例子：

Input : n = 2, m = 4, k = -1
Output : 8
Following configurations satisfy the conditions:-



Input  : n = 2, m = 1, k = -1
Output : The number of filling the matrix
         are 0

从以上条件可以看出, 矩阵中唯一可以输入的元素是1和-1。现在我们可以轻松推断出一些极端情况

如果k = -1, 则行和列数的总和不能为奇数, 因为-1将出现为奇数

因此, 如果每一行和每一列的次数为总和为奇数, 则答案为

0

.

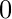
如果n = 1或m = 1, 则只有一种填充矩阵的方式, 因此答案为1。

如果以上情况均不适用, 则我们填写第一个

n-1

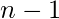
行和第一个

m-1

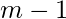
1和-1的列。然后, 由于已经知道每一行每一列的乘积, 因此可以唯一地标识其余数字, 因此答案是

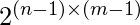
2 ^ {（n-1）\ times（m-1）}

C ++

// CPP program to find number of ways to fill
// a matrix under given constraints
#include <bits/stdc++.h>
using namespace std;
  
#define mod 100000007
  
/* Returns a raised power t under modulo mod */
long long modPower( long long a, long long t)
{
     long long now = a, ret = 1;
  
     // Counting number of ways of filling the matrix
     while (t) {
         if (t & 1)
             ret = now * (ret % mod);
         now = now * (now % mod);
         t >>= 1;
     }
     return ret;
}
  
// Function calculating the answer
long countWays( int n, int m, int k)
{
     // if sum of numbers of rows and columns is odd
     // i.e (n + m) % 2 == 1 and k = -1 then there
     // are 0 ways of filiing the matrix.
     if (k == -1 && (n + m) % 2 == 1)
         return 0;
  
     // If there is one row or one column then there
     // is only one way of filling the matrix
     if (n == 1 || m == 1)
         return 1;
  
     // If the above cases are not followed then we
     // find ways to fill the n - 1 rows and m - 1
     // columns which is 2 ^ ((m-1)*(n-1)).
     return (modPower(modPower(( long long )2, n - 1), m - 1) % mod);
}
  
// Driver function for the program
int main()
{
     int n = 2, m = 7, k = 1;
     cout << countWays(n, m, k);
     return 0;
}

输出如下：

64

Java

// Java program to find number of ways to fill
// a matrix under given constraints
import java.io.*;
  
class Example {
  
     final static long mod = 100000007 ;
  
     /* Returns a raised power t under modulo mod */
     static long modPower( long a, long t, long mod)
     {
         long now = a, ret = 1 ;
  
         // Counting number of ways of filling the
         // matrix
         while (t > 0 ) {
             if (t % 2 == 1 )
                 ret = now * (ret % mod);
             now = now * (now % mod);
             t >>= 1 ;
         }
         return ret;
     }
  
     // Function calculating the answer
     static long countWays( int n, int m, int k)
     {
         // if sum of numbers of rows and columns is
         // odd i.e (n + m) % 2 == 1 and k = -1, // then there are 0 ways of filiing the matrix.
         if (n == 1 || m == 1 )
             return 1 ;
  
         // If there is one row or one column then
         // there is only one way of filling the matrix
         else if ((n + m) % 2 == 1 && k == - 1 )
             return 0 ;
  
        // If the above cases are not followed then we
        // find ways to fill the n - 1 rows and m - 1
        // columns which is 2 ^ ((m-1)*(n-1)).
         return (modPower(modPower(( long ) 2 , n - 1 , mod), m - 1 , mod) % mod);
     }
  
     // Driver function for the program
     public static void main(String args[]) throws IOException
     {
         int n = 2 , m = 7 , k = 1 ;
         System.out.println(countWays(n, m, k));
     }
}

Python 3

# Python program to find number of ways to 
# fill a matrix under given constraints
  
# Returns a raised power t under modulo mod 
def modPower(a, t):
      
     now = a;
     ret = 1 ;
     mod = 100000007 ;
  
     # Counting number of ways of filling
     # the matrix
     while (t): 
         if (t & 1 ):
             ret = now * (ret % mod);
         now = now * (now % mod);
         t >> = 1 ;
      
     return ret;
  
# Function calculating the answer
def countWays(n, m, k):
  
     mod = 100000007 ;
      
     # if sum of numbers of rows and columns 
     # is odd i.e (n + m) % 2 == 1 and k = -1 
     # then there are 0 ways of filiing the matrix.
     if (k = = - 1 and ((n + m) % 2 = = 1 )):
         return 0 ;
  
     # If there is one row or one column then 
     # there is only one way of filling the matrix
     if (n = = 1 or m = = 1 ):
         return 1 ;
  
     # If the above cases are not followed then we
     # find ways to fill the n - 1 rows and m - 1
     # columns which is 2 ^ ((m-1)*(n-1)).
     return (modPower(modPower( 2 , n - 1 ), m - 1 ) % mod);
  
# Driver Code
n = 2 ;
m = 7 ;
k = 1 ;
print (countWays(n, m, k));
  
# This code is contributed 
# by Shivi_Aggarwal

C#

// C# program to find number of ways to fill
// a matrix under given constraints
using System;
  
class Example
{
  
     static long mod = 100000007;
  
     // Returns a raised power t 
     // under modulo mod 
     static long modPower( long a, long t, long mod)
     {
         long now = a, ret = 1;
  
         // Counting number of ways 
         // of filling the
         // matrix
         while (t > 0)
         {
             if (t % 2 == 1)
                 ret = now * (ret % mod);
             now = now * (now % mod);
             t >>= 1;
         }
         return ret;
     }
  
     // Function calculating the answer
     static long countWays( int n, int m, int k)
     {
         // if sum of numbers of rows 
         // and columns is odd i.e
         // (n + m) % 2 == 1 and 
         // k = -1, then there are 0 
         // ways of filiing the matrix.
         if (n == 1 || m == 1)
             return 1;
  
         // If there is one row or one
         // column then there is only 
         // one way of filling the matrix
         else if ((n + m) % 2 == 1 && k == -1)
             return 0;
  
         // If the above cases are not 
         // followed then we find ways
         // to fill the n - 1 rows and
         // m - 1 columns which is
         // 2 ^ ((m-1)*(n-1)).
         return (modPower(modPower(( long )2, n - 1, mod), m - 1, mod) % mod);
                                      
     }
  
     // Driver Code
     public static void Main() 
     {
         int n = 2, m = 7, k = 1;
         Console.WriteLine(countWays(n, m, k));
     }
}
  
// This code is contributed by vt_m.

的PHP

<?php
// PHP program to find number
// of ways to fill a matrix under
// given constraints
  
$mod = 100000007;
  
// Returns a raised power t 
// under modulo mod
function modPower( $a , $t )
{
     global $mod ;
     $now = $a ; $ret = 1;
  
     // Counting number of ways 
     // of filling the matrix
     while ( $t ) 
     {
         if ( $t & 1)
             $ret = $now * ( $ret % $mod );
         $now = $now * ( $now % $mod );
         $t >>= 1;
     }
     return $ret ;
}
  
// Function calculating the answer
function countWays( $n , $m , $k )
{
     global $mod ;
      
     // if sum of numbers of rows
     // and columns is odd i.e 
     // (n + m) % 2 == 1 and k = -1 
     // then there are 0 ways of 
     // filiing the matrix.
     if ( $k == -1 and ( $n + $m ) % 2 == 1)
         return 0;
  
     // If there is one row or
     // one column then there
     // is only one way of 
     // filling the matrix
     if ( $n == 1 or $m == 1)
         return 1;
  
     // If the above cases are
     // not followed then we
     // find ways to fill the 
     // n - 1 rows and m - 1
     // columns which is 
     // 2 ^ ((m-1)*(n-1)).
     return (modPower(modPower(2, $n - 1), $m - 1) % $mod );
}
  
     // Driver Code
     $n = 2; 
     $m = 7; 
     $k = 1;
     echo countWays( $n , $m , $k );
      
// This code is contributed by anuj_67.
?>

输出如下：

64

上述解决方案的时间复杂度为

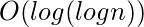
O（log（log n））
木子山

发表评论

:?: :razz: :sad: :evil: :!: :smile: :oops: :grin: :eek: :shock: :???: :cool: :lol: :mad: :twisted: :roll: :wink: :idea: :arrow: :neutral: :cry: :mrgreen: