算法题：全部为1的最大尺寸正方形子矩阵

2021年4月3日19:24:49 发表评论 888 次浏览

本文概述

给定一个二进制矩阵, 找出全为1的最大尺寸平方子矩阵。

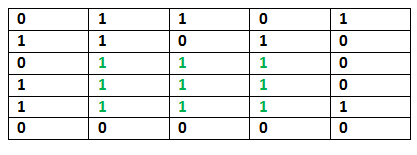
例如, 考虑下面的二进制矩阵。

最大尺寸的正方形子矩阵全1

算法：

令给定的二进制矩阵为M [R] [C]。该算法的思想是构造一个辅助大小矩阵S [] [], 其中每个条目S [i] [j]表示正方形子矩阵的大小, 其中所有1包括M [i] [j], 其中M [ i] [j]是子矩阵中最右边和最下面的条目。

1) Construct a sum matrix S[R][C] for the given M[R][C].
     a)    Copy first row and first columns as it is from M[][] to S[][]
     b)    For other entries, use following expressions to construct S[][]
         If M[i][j] is 1 then
            S[i][j] = min(S[i][j-1], S[i-1][j], S[i-1][j-1]) + 1
         Else /*If M[i][j] is 0*/
            S[i][j] = 0
2) Find the maximum entry in S[R][C]
3) Using the value and coordinates of maximum entry in S[i], print 
   sub-matrix of M[][]

对于上述示例中给定的M [R] [C], 构造的S [R] [C]将为：

0  1  1  0  1
   1  1  0  1  0
   0  1  1  1  0
   1  1  2  2  0
   1  2  2  3  1
   0  0  0  0  0

上述矩阵中最大条目的值为3, 条目的坐标为(4, 3)。使用最大值及其坐标, 我们可以找到所需的子矩阵。

C++

// C++ code for Maximum size square 
// sub-matrix with all 1s 
#include <bits/stdc++.h>
#define bool int 
#define R 6 
#define C 5 
using namespace std;
  
  
void printMaxSubSquare( bool M[R][C]) 
{ 
     int i, j; 
     int S[R][C]; 
     int max_of_s, max_i, max_j; 
      
     /* Set first column of S[][]*/
     for (i = 0; i < R; i++) 
         S[i][0] = M[i][0]; 
      
     /* Set first row of S[][]*/
     for (j = 0; j < C; j++) 
         S[0][j] = M[0][j]; 
          
     /* Construct other entries of S[][]*/
     for (i = 1; i < R; i++) 
     { 
         for (j = 1; j < C; j++) 
         { 
             if (M[i][j] == 1) 
                 S[i][j] = min(S[i][j-1], min( S[i-1][j], S[i-1][j-1])) + 1; 
             else
                 S[i][j] = 0; 
         } 
     } 
      
     /* Find the maximum entry, and indexes of maximum entry 
         in S[][] */
     max_of_s = S[0][0]; max_i = 0; max_j = 0; 
     for (i = 0; i < R; i++) 
     { 
         for (j = 0; j < C; j++) 
         { 
             if (max_of_s < S[i][j]) 
             { 
                 max_of_s = S[i][j]; 
                 max_i = i; 
                 max_j = j; 
             } 
         }             
     } 
  
     cout<< "Maximum size sub-matrix is: \n" ; 
     for (i = max_i; i > max_i - max_of_s; i--) 
     { 
         for (j = max_j; j > max_j - max_of_s; j--) 
         { 
             cout << M[i][j] << " " ; 
         } 
         cout << "\n" ; 
     } 
} 
  
  
/* Driver code */
int main() 
{ 
     bool M[R][C] = {{0, 1, 1, 0, 1}, {1, 1, 0, 1, 0}, {0, 1, 1, 1, 0}, {1, 1, 1, 1, 0}, {1, 1, 1, 1, 1}, {0, 0, 0, 0, 0}}; 
                      
     printMaxSubSquare(M); 
} 
  
// This is code is contributed by rathbhupendra

C

// C code for Maximum size square 
// sub-matrix with all 1s
#include<stdio.h>
#define bool int
#define R 6
#define C 5
  
void printMaxSubSquare( bool M[R][C])
{
int i, j;
int S[R][C];
int max_of_s, max_i, max_j; 
  
/* Set first column of S[][]*/
for (i = 0; i < R; i++)
     S[i][0] = M[i][0];
  
/* Set first row of S[][]*/    
for (j = 0; j < C; j++)
     S[0][j] = M[0][j];
      
/* Construct other entries of S[][]*/
for (i = 1; i < R; i++)
{
     for (j = 1; j < C; j++)
     {
     if (M[i][j] == 1) 
         S[i][j] = min(S[i][j-1], S[i-1][j], S[i-1][j-1]) + 1;
     else
         S[i][j] = 0;
     } 
} 
  
/* Find the maximum entry, and indexes of maximum entry 
     in S[][] */
max_of_s = S[0][0]; max_i = 0; max_j = 0;
for (i = 0; i < R; i++)
{
     for (j = 0; j < C; j++)
     {
     if (max_of_s < S[i][j])
     {
         max_of_s = S[i][j];
         max_i = i; 
         max_j = j;
     }     
     }                 
}     
  
printf ( "Maximum size sub-matrix is: \n" );
for (i = max_i; i > max_i - max_of_s; i--)
{
     for (j = max_j; j > max_j - max_of_s; j--)
     {
     printf ( "%d " , M[i][j]);
     } 
     printf ( "\n" );
} 
}     
  
/* UTILITY FUNCTIONS */
/* Function to get minimum of three values */
int min( int a, int b, int c)
{
int m = a;
if (m > b) 
     m = b;
if (m > c) 
     m = c;
return m;
}
  
/* Driver function to test above functions */
int main()
{
bool M[R][C] = {{0, 1, 1, 0, 1}, {1, 1, 0, 1, 0}, {0, 1, 1, 1, 0}, {1, 1, 1, 1, 0}, {1, 1, 1, 1, 1}, {0, 0, 0, 0, 0}};
                  
printMaxSubSquare(M);
getchar (); 
}

Java

// JAVA Code for Maximum size square 
// sub-matrix with all 1s
public class GFG
{
     // method for Maximum size square sub-matrix with all 1s
     static void printMaxSubSquare( int M[][])
     {
         int i, j;
         int R = M.length;         //no of rows in M[][]
         int C = M[ 0 ].length;     //no of columns in M[][]
         int S[][] = new int [R][C];     
          
         int max_of_s, max_i, max_j; 
      
         /* Set first column of S[][]*/
         for (i = 0 ; i < R; i++)
             S[i][ 0 ] = M[i][ 0 ];
      
         /* Set first row of S[][]*/
         for (j = 0 ; j < C; j++)
             S[ 0 ][j] = M[ 0 ][j];
          
         /* Construct other entries of S[][]*/
         for (i = 1 ; i < R; i++)
         {
             for (j = 1 ; j < C; j++)
             {
                 if (M[i][j] == 1 ) 
                     S[i][j] = Math.min(S[i][j- 1 ], Math.min(S[i- 1 ][j], S[i- 1 ][j- 1 ])) + 1 ;
                 else
                     S[i][j] = 0 ;
             } 
         }     
          
         /* Find the maximum entry, and indexes of maximum entry 
             in S[][] */
         max_of_s = S[ 0 ][ 0 ]; max_i = 0 ; max_j = 0 ;
         for (i = 0 ; i < R; i++)
         {
             for (j = 0 ; j < C; j++)
             {
                 if (max_of_s < S[i][j])
                 {
                     max_of_s = S[i][j];
                     max_i = i; 
                     max_j = j;
                 }     
             }                 
         }     
          
         System.out.println( "Maximum size sub-matrix is: " );
         for (i = max_i; i > max_i - max_of_s; i--)
         {
             for (j = max_j; j > max_j - max_of_s; j--)
             {
                 System.out.print(M[i][j] + " " );
             } 
             System.out.println();
         } 
     } 
      
     // Driver program 
     public static void main(String[] args) 
     {
         int M[][] = {{ 0 , 1 , 1 , 0 , 1 }, { 1 , 1 , 0 , 1 , 0 }, { 0 , 1 , 1 , 1 , 0 }, { 1 , 1 , 1 , 1 , 0 }, { 1 , 1 , 1 , 1 , 1 }, { 0 , 0 , 0 , 0 , 0 }};
              
         printMaxSubSquare(M);
     }
  
}

Python3

# Python3 code for Maximum size
# square sub-matrix with all 1s
  
def printMaxSubSquare(M):
     R = len (M) # no. of rows in M[][]
     C = len (M[ 0 ]) # no. of columns in M[][]
  
     S = [[ 0 for k in range (C)] for l in range (R)]
     # here we have set the first row and column of S[][]
  
     # Construct other entries
     for i in range ( 1 , R):
         for j in range ( 1 , C):
             if (M[i][j] = = 1 ):
                 S[i][j] = min (S[i][j - 1 ], S[i - 1 ][j], S[i - 1 ][j - 1 ]) + 1
             else :
                 S[i][j] = 0
      
     # Find the maximum entry and
     # indices of maximum entry in S[][]
     max_of_s = S[ 0 ][ 0 ]
     max_i = 0
     max_j = 0
     for i in range (R):
         for j in range (C):
             if (max_of_s < S[i][j]):
                 max_of_s = S[i][j]
                 max_i = i
                 max_j = j
  
     print ( "Maximum size sub-matrix is: " )
     for i in range (max_i, max_i - max_of_s, - 1 ):
         for j in range (max_j, max_j - max_of_s, - 1 ):
             print (M[i][j], end = " " )
         print ("")
  
# Driver Program
M = [[ 0 , 1 , 1 , 0 , 1 ], [ 1 , 1 , 0 , 1 , 0 ], [ 0 , 1 , 1 , 1 , 0 ], [ 1 , 1 , 1 , 1 , 0 ], [ 1 , 1 , 1 , 1 , 1 ], [ 0 , 0 , 0 , 0 , 0 ]]
  
printMaxSubSquare(M)
  
# This code is contributed by Soumen Ghosh

C#

// C# Code for Maximum size square 
// sub-matrix with all 1s
  
using System;
  
  
public class GFG
{
     // method for Maximum size square sub-matrix with all 1s
     static void printMaxSubSquare( int [, ]M)
     {
         int i, j;
         //no of rows in M[, ]
         int R = M.GetLength(0);    
          //no of columns in M[, ]
         int C = M.GetLength(1);    
         int [, ]S = new int [R, C];     
          
         int max_of_s, max_i, max_j; 
          
         /* Set first column of S[, ]*/
         for (i = 0; i < R; i++)
             S[i, 0] = M[i, 0];
          
         /* Set first row of S[][]*/
         for (j = 0; j < C; j++)
             S[0, j] = M[0, j];
              
         /* Construct other entries of S[, ]*/
         for (i = 1; i < R; i++)
         {
             for (j = 1; j < C; j++)
             {
                 if (M[i, j] == 1) 
                     S[i, j] = Math.Min(S[i, j-1], Math.Min(S[i-1, j], S[i-1, j-1])) + 1;
                 else
                     S[i, j] = 0;
             } 
         }     
          
         /* Find the maximum entry, and indexes of 
             maximum entry in S[, ] */
         max_of_s = S[0, 0]; max_i = 0; max_j = 0;
         for (i = 0; i < R; i++)
         {
             for (j = 0; j < C; j++)
             {
                 if (max_of_s < S[i, j])
                 {
                     max_of_s = S[i, j];
                     max_i = i; 
                     max_j = j;
                 }     
             }                 
         }     
          
         Console.WriteLine( "Maximum size sub-matrix is: " );
         for (i = max_i; i > max_i - max_of_s; i--)
         {
             for (j = max_j; j > max_j - max_of_s; j--)
             {
                 Console.Write(M[i, j] + " " );
             } 
             Console.WriteLine();
         } 
     } 
      
     // Driver program 
     public static void Main() 
     {
         int [, ]M = new int [6, 5]{{0, 1, 1, 0, 1}, {1, 1, 0, 1, 0}, {0, 1, 1, 1, 0}, {1, 1, 1, 1, 0}, {1, 1, 1, 1, 1}, {0, 0, 0, 0, 0}};
              
         printMaxSubSquare(M);
     }
  
}

的PHP

<?php
// PHP code for Maximum size square 
// sub-matrix with all 1s 
  
function printMaxSubSquare( $M , $R , $C ) 
{ 
     $S = array ( array ()) ;
  
     /* Set first column of S[][]*/
     for ( $i = 0; $i < $R ; $i ++) 
         $S [ $i ][0] = $M [ $i ][0]; 
      
     /* Set first row of S[][]*/
     for ( $j = 0; $j < $C ; $j ++) 
         $S [0][ $j ] = $M [0][ $j ]; 
          
     /* Construct other entries of S[][]*/
     for ( $i = 1; $i < $R ; $i ++) 
     { 
         for ( $j = 1; $j < $C ; $j ++) 
         { 
             if ( $M [ $i ][ $j ] == 1) 
                 $S [ $i ][ $j ] = min( $S [ $i ][ $j - 1], $S [ $i - 1][ $j ], $S [ $i - 1][ $j - 1]) + 1; 
             else
                 $S [ $i ][ $j ] = 0; 
         } 
     } 
      
     /* Find the maximum entry, and indexes 
     of maximum entry in S[][] */
     $max_of_s = $S [0][0];
     $max_i = 0; 
     $max_j = 0; 
     for ( $i = 0; $i < $R ; $i ++) 
     { 
         for ( $j = 0; $j < $C ; $j ++) 
         { 
         if ( $max_of_s < $S [ $i ][ $j ]) 
         { 
             $max_of_s = $S [ $i ][ $j ]; 
             $max_i = $i ; 
             $max_j = $j ; 
         } 
         }             
     } 
      
     printf( "Maximum size sub-matrix is: \n" ); 
     for ( $i = $max_i ; 
         $i > $max_i - $max_of_s ; $i --) 
     { 
         for ( $j = $max_j ; 
             $j > $max_j - $max_of_s ; $j --) 
         { 
             echo $M [ $i ][ $j ], " " ; 
         } 
         echo "\n" ;
     } 
} 
  
# Driver code
$M = array ( array (0, 1, 1, 0, 1), array (1, 1, 0, 1, 0), array (0, 1, 1, 1, 0), array (1, 1, 1, 1, 0), array (1, 1, 1, 1, 1), array (0, 0, 0, 0, 0)); 
      
$R = 6 ;
$C = 5 ;         
printMaxSubSquare( $M , $R , $C ); 
  
// This code is contributed by Ryuga
?>

输出如下：

Maximum size sub-matrix is: 
1 1 1 
1 1 1 
1 1 1

时间复杂度：O(m * n)其中m是给定矩阵中的行数, n是列数。

辅助空间：O(m * n)其中m是给定矩阵中的行数, n是列数。

算法范例：动态规划

如果你发现上述代码/算法中的任何错误, 或找到其他解决相同问题的方法, 请发表评论

木子山

发表评论

:?: :razz: :sad: :evil: :!: :smile: :oops: :grin: :eek: :shock: :???: :cool: :lol: :mad: :twisted: :roll: :wink: :idea: :arrow: :neutral: :cry: :mrgreen: