合并排序解析和实现详细指南

2021年4月2日12:03:20 发表评论 626 次浏览

本文概述

像快速排序, 合并排序是一个分治算法。它将输入数组分为两个半部分, 将自身称为两个半部分, 然后合并两个已排序的半个部分。merge()函数用于合并两半。 merge(arr, l, m, r)是一个关键过程, 假定对arr [l..m]和arr [m + 1..r]进行排序并将两个排序后的子数组合并为一个。有关详细信息, 请参见以下C实现。

MergeSort(arr[], l, r)
If r > l
     1. Find the middle point to divide the array into two halves:  
             middle m = (l+r)/2
     2. Call mergeSort for first half:   
             Call mergeSort(arr, l, m)
     3. Call mergeSort for second half:
             Call mergeSort(arr, m+1, r)
     4. Merge the two halves sorted in step 2 and 3:
             Call merge(arr, l, m, r)

下图来自

维基百科

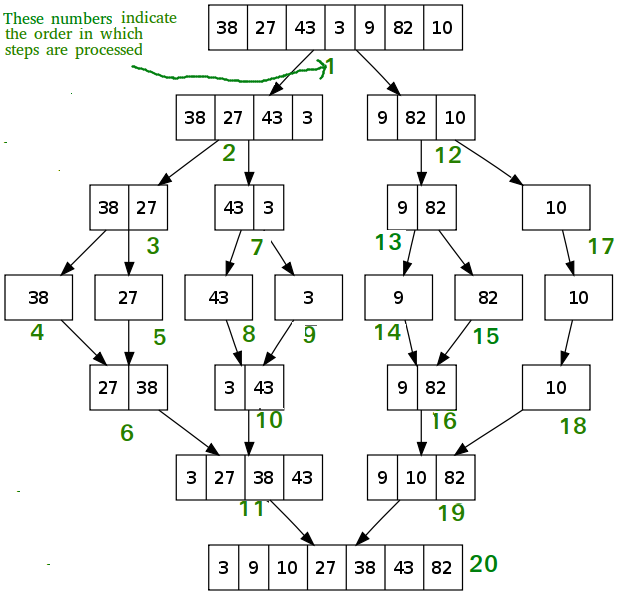
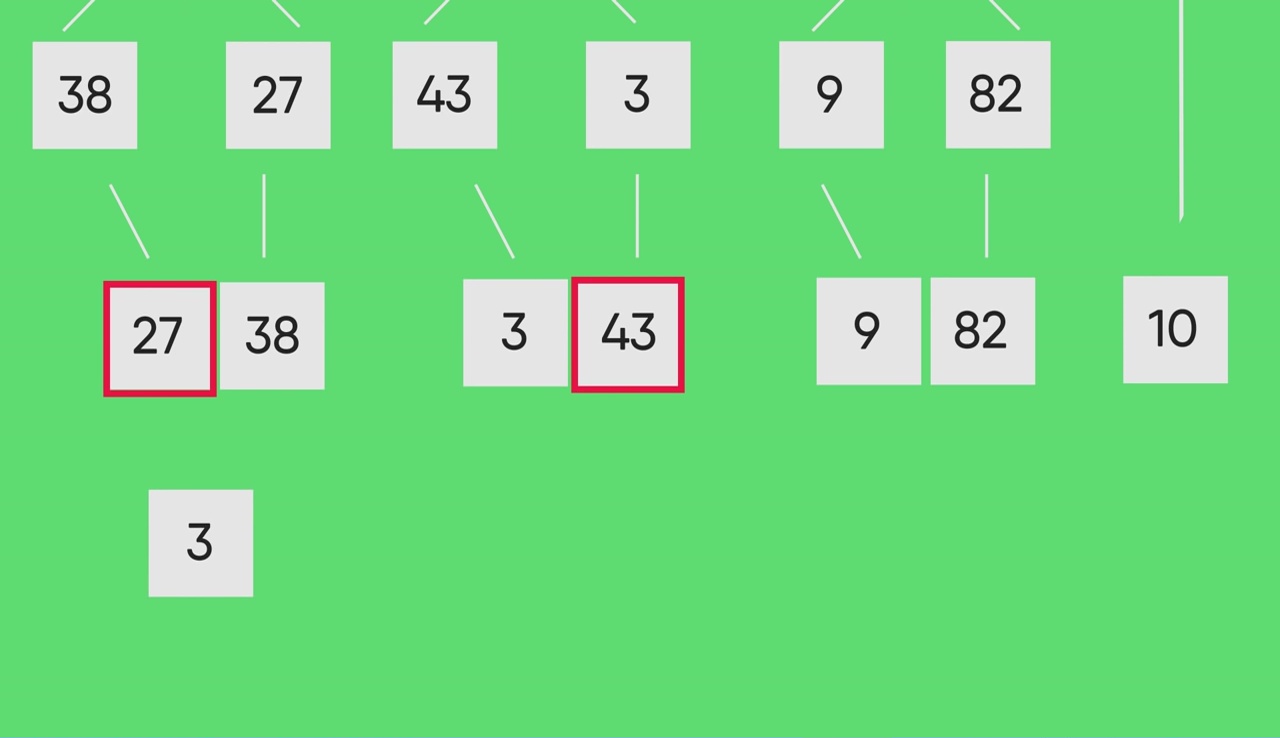
显示了示例数组{38、27、43、3、9、82、10}的完整合并排序过程。如果仔细看一下图, 我们可以看到将数组递归地分成两半, 直到大小变为1。一旦大小变为1, 合并过程便开始起作用, 并开始合并数组直到完整的数组成为合并。

合并排序教程

C ++

// C++ program for Merge Sort
#include<iostream>
using namespace std;
 
// Merges two subarrays of arr[].
// First subarray is arr[l..m]
// Second subarray is arr[m+1..r]
void merge( int arr[], int l, int m, int r)
{
     int n1 = m - l + 1;
     int n2 = r - m;
 
     // Create temp arrays
     int L[n1], R[n2];
 
     // Copy data to temp arrays L[] and R[]
     for ( int i = 0; i < n1; i++)
         L[i] = arr[l + i];
     for ( int j = 0; j < n2; j++)
         R[j] = arr[m + 1 + j];
 
     // Merge the temp arrays back into arr[l..r]
     
     // Initial index of first subarray
     int i = 0;
     
     // Initial index of second subarray
     int j = 0;
     
     // Initial index of merged subarray
     int k = l;
     
     while (i < n1 && j < n2)
     {
         if (L[i] <= R[j])
         {
             arr[k] = L[i];
             i++;
         }
         else
         {
             arr[k] = R[j];
             j++;
         }
         k++;
     }
 
     // Copy the remaining elements of
     // L[], if there are any
     while (i < n1)
     {
         arr[k] = L[i];
         i++;
         k++;
     }
 
     // Copy the remaining elements of
     // R[], if there are any
     while (j < n2)
     {
         arr[k] = R[j];
         j++;
         k++;
     }
}
 
// l is for left index and r is
// right index of the sub-array
// of arr to be sorted */
void mergeSort( int arr[], int l, int r)
{
     if (l < r)
     {
         
         // Same as (l+r)/2, but avoids
         // overflow for large l and h
         int m = l + (r - l) / 2;
 
         // Sort first and second halves
         mergeSort(arr, l, m);
         mergeSort(arr, m + 1, r);
 
         merge(arr, l, m, r);
     }
}
 
// UTILITY FUNCTIONS
// Function to print an array
void printArray( int A[], int size)
{
     for ( int i = 0; i < size; i++)
         cout << A[i] << " " ;
}
 
// Driver code
int main()
{
     int arr[] = { 12, 11, 13, 5, 6, 7 };
     int arr_size = sizeof (arr) / sizeof (arr[0]);
 
     cout << "Given array is \n" ;
     printArray(arr, arr_size);
 
     mergeSort(arr, 0, arr_size - 1);
 
     cout << "\nSorted array is \n" ;
     printArray(arr, arr_size);
     return 0;
}
 
// This code is contributed by Mayank Tyagi

C

/* C program for Merge Sort */
#include <stdio.h>
#include <stdlib.h>
 
// Merges two subarrays of arr[].
// First subarray is arr[l..m]
// Second subarray is arr[m+1..r]
void merge( int arr[], int l, int m, int r)
{
     int i, j, k;
     int n1 = m - l + 1;
     int n2 = r - m;
 
     /* create temp arrays */
     int L[n1], R[n2];
 
     /* Copy data to temp arrays L[] and R[] */
     for (i = 0; i < n1; i++)
         L[i] = arr[l + i];
     for (j = 0; j < n2; j++)
         R[j] = arr[m + 1 + j];
 
     /* Merge the temp arrays back into arr[l..r]*/
     i = 0; // Initial index of first subarray
     j = 0; // Initial index of second subarray
     k = l; // Initial index of merged subarray
     while (i < n1 && j < n2) {
         if (L[i] <= R[j]) {
             arr[k] = L[i];
             i++;
         }
         else {
             arr[k] = R[j];
             j++;
         }
         k++;
     }
 
     /* Copy the remaining elements of L[], if there
     are any */
     while (i < n1) {
         arr[k] = L[i];
         i++;
         k++;
     }
 
     /* Copy the remaining elements of R[], if there
     are any */
     while (j < n2) {
         arr[k] = R[j];
         j++;
         k++;
     }
}
 
/* l is for left index and r is right index of the
sub-array of arr to be sorted */
void mergeSort( int arr[], int l, int r)
{
     if (l < r) {
         // Same as (l+r)/2, but avoids overflow for
         // large l and h
         int m = l + (r - l) / 2;
 
         // Sort first and second halves
         mergeSort(arr, l, m);
         mergeSort(arr, m + 1, r);
 
         merge(arr, l, m, r);
     }
}
 
/* UTILITY FUNCTIONS */
/* Function to print an array */
void printArray( int A[], int size)
{
     int i;
     for (i = 0; i < size; i++)
         printf ( "%d " , A[i]);
     printf ( "\n" );
}
 
/* Driver program to test above functions */
int main()
{
     int arr[] = { 12, 11, 13, 5, 6, 7 };
     int arr_size = sizeof (arr) / sizeof (arr[0]);
 
     printf ( "Given array is \n" );
     printArray(arr, arr_size);
 
     mergeSort(arr, 0, arr_size - 1);
 
     printf ( "\nSorted array is \n" );
     printArray(arr, arr_size);
     return 0;
}

Java

/* Java program for Merge Sort */
class MergeSort {
     // Merges two subarrays of arr[].
     // First subarray is arr[l..m]
     // Second subarray is arr[m+1..r]
     void merge( int arr[], int l, int m, int r)
     {
         // Find sizes of two subarrays to be merged
         int n1 = m - l + 1 ;
         int n2 = r - m;
 
         /* Create temp arrays */
         int L[] = new int [n1];
         int R[] = new int [n2];
 
         /*Copy data to temp arrays*/
         for ( int i = 0 ; i < n1; ++i)
             L[i] = arr[l + i];
         for ( int j = 0 ; j < n2; ++j)
             R[j] = arr[m + 1 + j];
 
         /* Merge the temp arrays */
 
         // Initial indexes of first and second subarrays
         int i = 0 , j = 0 ;
 
         // Initial index of merged subarry array
         int k = l;
         while (i < n1 && j < n2) {
             if (L[i] <= R[j]) {
                 arr[k] = L[i];
                 i++;
             }
             else {
                 arr[k] = R[j];
                 j++;
             }
             k++;
         }
 
         /* Copy remaining elements of L[] if any */
         while (i < n1) {
             arr[k] = L[i];
             i++;
             k++;
         }
 
         /* Copy remaining elements of R[] if any */
         while (j < n2) {
             arr[k] = R[j];
             j++;
             k++;
         }
     }
 
     // Main function that sorts arr[l..r] using
     // merge()
     void sort( int arr[], int l, int r)
     {
         if (l < r) {
             // Find the middle point
             int m = (l + r) / 2 ;
 
             // Sort first and second halves
             sort(arr, l, m);
             sort(arr, m + 1 , r);
 
             // Merge the sorted halves
             merge(arr, l, m, r);
         }
     }
 
     /* A utility function to print array of size n */
     static void printArray( int arr[])
     {
         int n = arr.length;
         for ( int i = 0 ; i < n; ++i)
             System.out.print(arr[i] + " " );
         System.out.println();
     }
 
     // Driver method
     public static void main(String args[])
     {
         int arr[] = { 12 , 11 , 13 , 5 , 6 , 7 };
 
         System.out.println( "Given Array" );
         printArray(arr);
 
         MergeSort ob = new MergeSort();
         ob.sort(arr, 0 , arr.length - 1 );
 
         System.out.println( "\nSorted array" );
         printArray(arr);
     }
}
/* This code is contributed by Rajat Mishra */

Python3

# Python program for implementation of MergeSort
def mergeSort(arr):
     if len (arr) > 1 :
         mid = len (arr) / / 2 # Finding the mid of the array
         L = arr[:mid] # Dividing the array elements
         R = arr[mid:] # into 2 halves
 
         mergeSort(L) # Sorting the first half
         mergeSort(R) # Sorting the second half
 
         i = j = k = 0
         
         # Copy data to temp arrays L[] and R[]
         while i < len (L) and j < len (R):
             if L[i] < R[j]:
                 arr[k] = L[i]
                 i + = 1
             else :
                 arr[k] = R[j]
                 j + = 1
             k + = 1
         
         # Checking if any element was left
         while i < len (L):
             arr[k] = L[i]
             i + = 1
             k + = 1
         
         while j < len (R):
             arr[k] = R[j]
             j + = 1
             k + = 1
 
# Code to print the list
def printList(arr):
     for i in range ( len (arr)):       
         print (arr[i], end = " " )
     print ()
 
# driver code to test the above code
if __name__ = = '__main__' :
     arr = [ 12 , 11 , 13 , 5 , 6 , 7 ]
     print ( "Given array is" , end = "\n" )
     printList(arr)
     mergeSort(arr)
     print ( "Sorted array is: " , end = "\n" )
     printList(arr)
 
# This code is contributed by Mayank Khanna

Python3(替代)

# Python program for implementation of 
# MergeSort (Alternative)

def merge_sort(values):

    if len(values)>1:
        m = len(values)//2
        left = values[:m]
        right = values[m:]
        left = merge_sort(left)
        right = merge_sort(right)

        values =[]

        while len(left)>0 and len(right)>0:
            if left[0]<right[0]:
                values.append(left[0])
                left.pop(0)
            else:
                values.append(right[0])
                right.pop(0)

        for i in left:
            values.append(i)
        for i in right:
            values.append(i)
                
    return values

# Input list
a = [12, 11, 13, 5, 6, 7]
print("Given array is")
print(*a)

a = merge_sort(a)

# Print output
print("Sorted array is : ")
print(*a)

# This code is contributed by Marco Lam

C#

// C# program for Merge Sort
using System;
class MergeSort{
     
// Merges two subarrays of []arr.
// First subarray is arr[l..m]
// Second subarray is arr[m+1..r]
void merge( int []arr, int l, int m, int r)
{
   // Find sizes of two
   // subarrays to be merged
   int n1 = m - l + 1;
   int n2 = r - m;
 
   // Create temp arrays
   int []L = new int [n1];
   int []R = new int [n2];
   int i, j;
   
   // Copy data to temp arrays
   for (i = 0; i < n1; ++i)
     L[i] = arr[l + i];
   for (j = 0; j < n2; ++j)
     R[j] = arr[m + 1 + j];
 
   // Merge the temp arrays
 
   // Initial indexes of first
   // and second subarrays
   i = 0;
   j = 0;
 
   // Initial index of merged
   // subarry array
   int k = l;
   while (i < n1 && j < n2)
   {
     if (L[i] <= R[j])
     {
       arr[k] = L[i];
       i++;
     }
     else
     {
       arr[k] = R[j];
       j++;
     }
     k++;
   }
 
   // Copy remaining elements
   // of L[] if any
   while (i < n1)
   {
     arr[k] = L[i];
     i++;
     k++;
   }
 
   // Copy remaining elements
   // of R[] if any
   while (j < n2)
   {
     arr[k] = R[j];
     j++;
     k++;
   }
}
 
// Main function that
// sorts arr[l..r] using
// merge()
void sort( int []arr, int l, int r)
{
   if (l < r)
   {
     // Find the middle
     // point
     int m = (l + r) / 2;
 
     // Sort first and
     // second halves
     sort(arr, l, m);
     sort(arr, m + 1, r);
 
     // Merge the sorted halves
     merge(arr, l, m, r);
   }
}
 
// A utility function to
// print array of size n */
static void printArray( int []arr)
{
   int n = arr.Length;
   for ( int i = 0; i < n; ++i)
     Console.Write(arr[i] + " " );
   Console.WriteLine();
}
 
// Driver method
public static void Main(String []args)
{
   int []arr = {12, 11, 13, 5, 6, 7};
   Console.WriteLine( "Given Array" );
   printArray(arr);
   MergeSort ob = new MergeSort();
   ob.sort(arr, 0, arr.Length - 1);
   Console.WriteLine( "\nSorted array" );
   printArray(arr);
}
}
 
// This code is contributed by Princi Singh

输出如下：

Given array is
12 11 13 5 6 7

Sorted array is
5 6 7 11 12 13

时间复杂度：

在不同机器上对数组进行排序。合并排序是一种递归算法, 时间复杂度可以表示为以下递归关系。

T(n)= 2T(n / 2)+θ(n)

可以使用"递归树"方法或"主"方法解决以上重复问题。它属于主方法的情况II, 递归的解为θ(nLogn)。在所有3种情况下(最差, 平均和最佳), 合并排序的时间复杂度均为θ(nLogn), 因为合并排序始终将数组分为两半, 并花费线性时间来合并两半。

辅助空间：O(n)

算法范式：分治算法

就地排序：在典型的实现中没有

稳定：是

合并排序的应用 

  1. 合并排序对于以O(nLogn)时间排序链接列表很有用对于链表, 情况有所不同, 主要是由于数组和链表的内存分配不同。与数组不同, 链接列表节点在内存中可能不相邻。与数组不同, 在链表中, 我们可以在O(1)额外空间和O(1)时间的中间插入项目。因此, 可以实现合并排序的合并操作而不必为链接列表增加空间。
    在数组中, 由于元素在内存中是连续的, 因此我们可以进行随机访问。假设我们有一个整数(4字节)数组A, 并且将A [0]的地址设为x, 然后访问A [i], 我们可以直接访问(x + i * 4)处的内存。与数组不同, 我们不能在链表中进行随机访问。快速排序需要很多此类访问权限。在访问第i个索引的链表中, 我们没有从头到第i个节点的每个节点, 因为我们没有连续的内存块。因此, 快速排序的开销增加了。合并排序顺序访问数据, 并且对随机访问的需求低。
  2. 倒数计数问题
  3. 用于外部分类

合并排序图解：

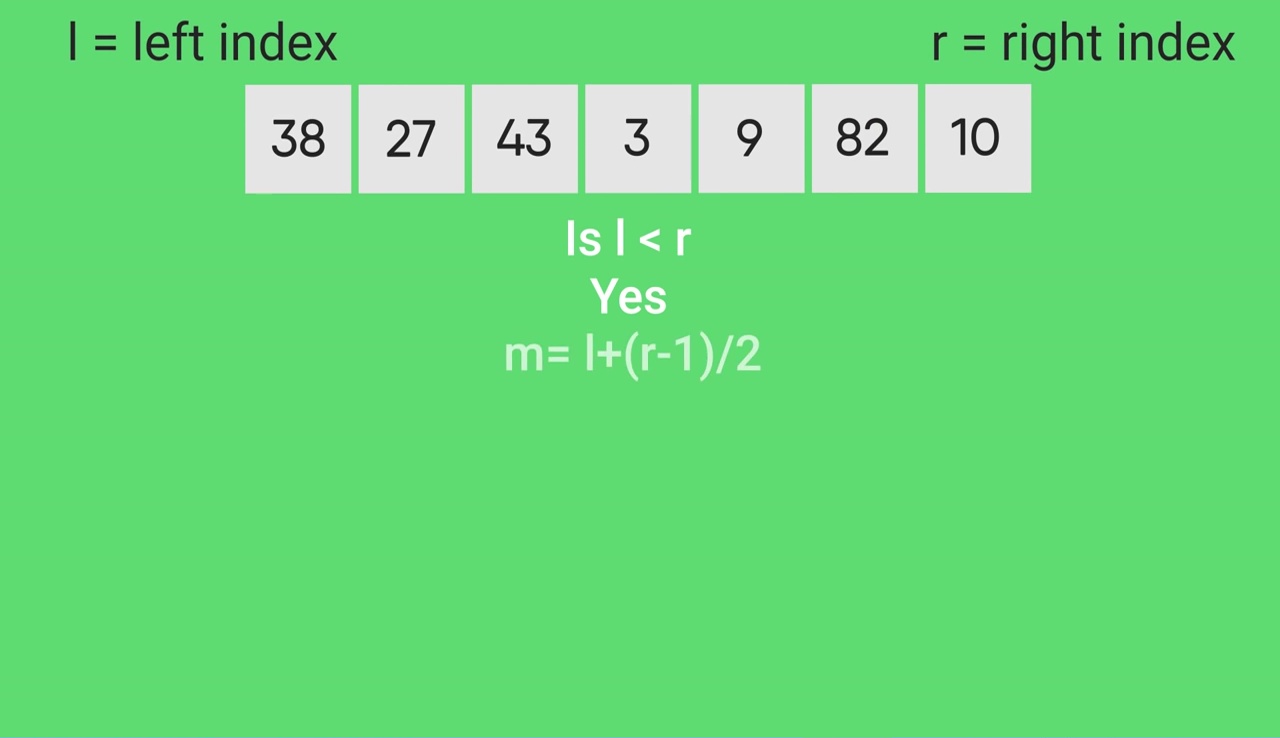
合并排序1
合并排序2
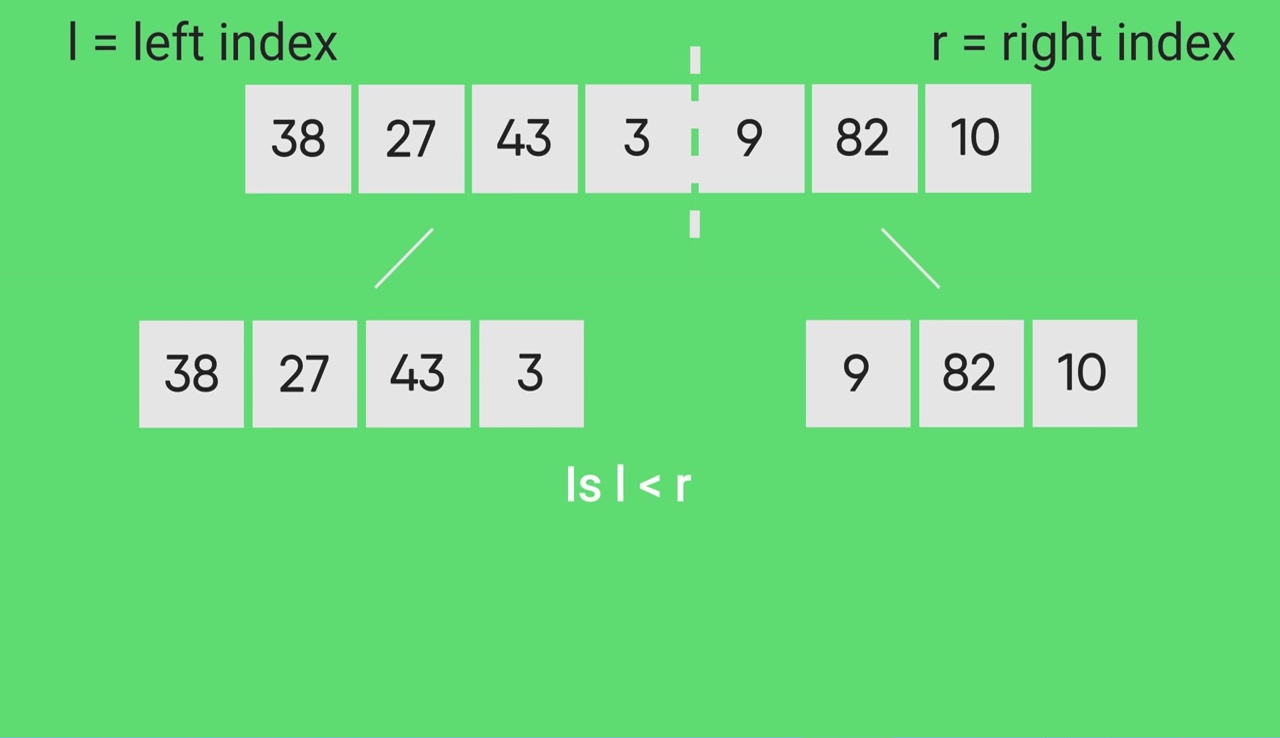
合并排序3
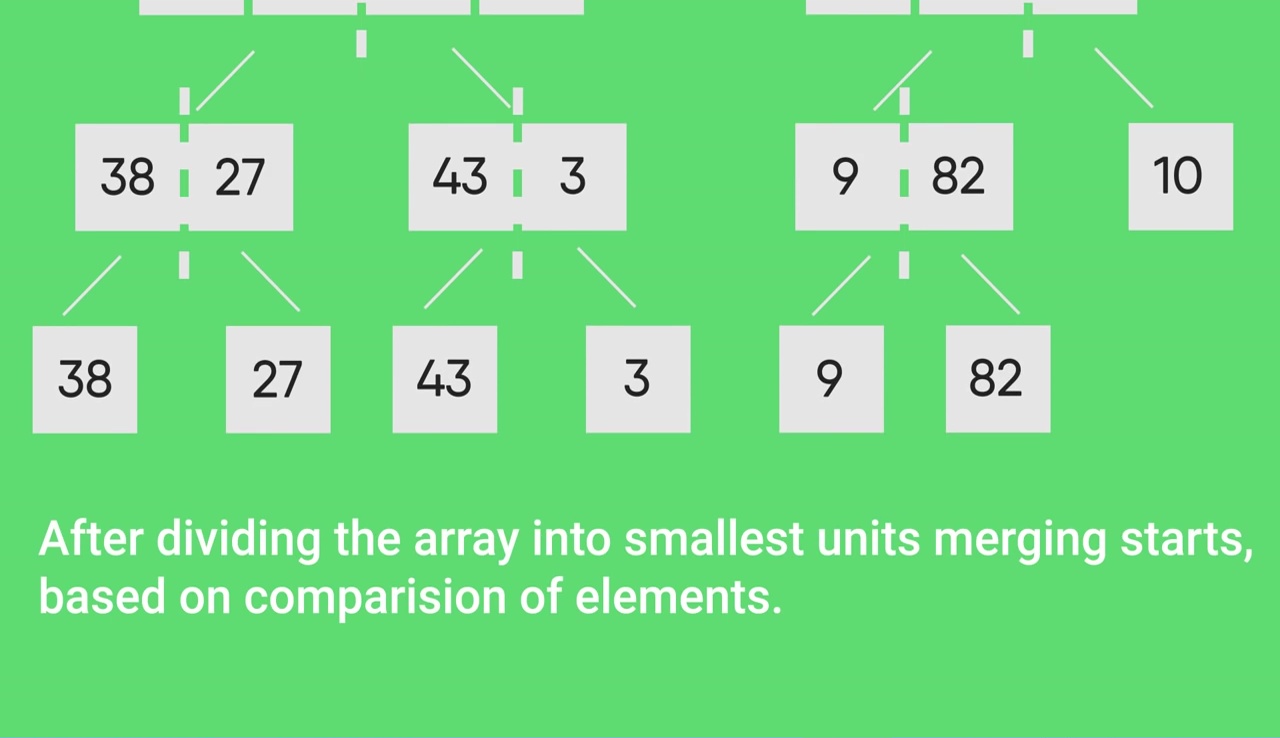
合并排序4
合并排序5
合并排序6
  • 关于合并排序的最新文章
  • 排序的编码实践。
  • 合并排序测验

如果发现任何不正确的地方, 或者想分享有关上述主题的更多信息, 请写评论。

木子山

发表评论

:?: :razz: :sad: :evil: :!: :smile: :oops: :grin: :eek: :shock: :???: :cool: :lol: :mad: :twisted: :roll: :wink: :idea: :arrow: :neutral: :cry: :mrgreen: