的方框图组合逻辑电路:

组合逻辑电路要记住的要点:
- 输出取决于输入的组合。
- 输出仅是当前输入的纯函数, 即, 先前状态输入不会对输出产生任何影响。另外, 它不占用内存。
- 换一种说法,
OUTPUT=f(INPUT)
- 输入被称为来自电路的激励, 输出被称为组合逻辑电路的响应。
组合逻辑电路的分类:
1.算术:
2.数据处理:
- 多路复用器
- 解复用器
- 编码器和解码器
3.代码转换器:
- BCD到Excess-3代码, 反之亦然
- BCD转换为格雷码, 反之亦然
- 七段
半加法器和全加法器的设计:
- 将两个位相加的组合逻辑电路称为Half Adder。
- 执行三个单位加法的组合逻辑电路称为全加器。
1.半加法器:
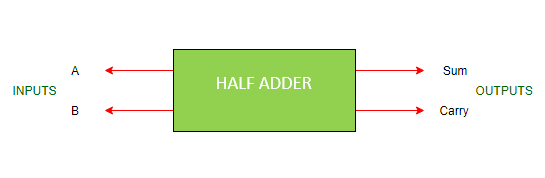
- 它是一种算术组合逻辑电路, 旨在执行两个单位的加法运算。
- 它包含两个输入并产生两个输出。
- 输入称为" Augend"和" Added"位, 而输出称为" Sum and Carry"。
让我们观察一下一位加法,
0+0=0
0+1=1
1+0=1
1+1=10由于1 + 1 = 10, 结果必须是两位输出。所以, 上面可以改写成
0+0=00
0+1=01
1+0=01
1+1=101 + 1的结果是10, 其中" 1"是进位输出(C出), " 0"是总和输出(常规输出)。
半加器真值表:
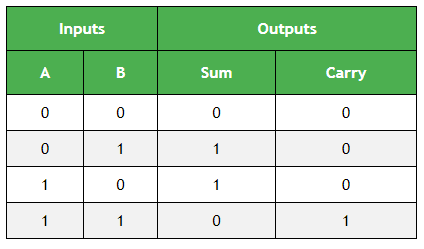
下一步是绘制逻辑图。要绘制逻辑图, 我们需要布尔表达式, 可以使用K地图(卡诺地图)。由于有两个输出变量" S"和" C", 因此我们需要为每个输出变量定义K-map。
输出变量总和" S"的K映射:
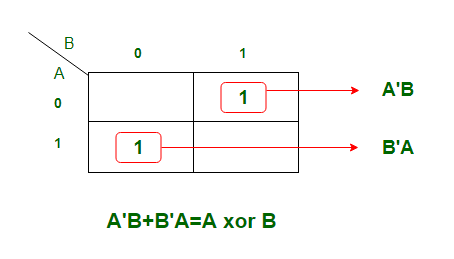
K图是产品总和形成。得到的方程是
S = AB' + A'B在逻辑上可以写成
S = A xor B输出变量的K映射携带" C":
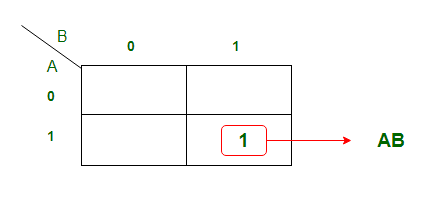
从K-map得到的方程是
C = AB使用布尔表达式, 我们可以绘制如下逻辑图。
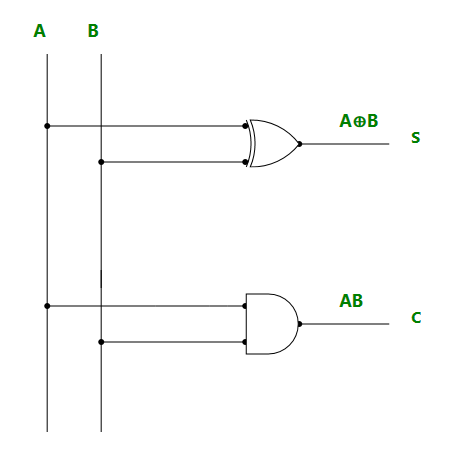
局限性:
Half加法器中无法进行进位加法。
2.完全加法器:

- 为了克服半加器面临的上述限制, 实现了全加器。
- 它是一种算术组合逻辑电路, 执行三个位的加法运算。
- 它包含三个输入(A, B, Cin)并产生两个输出(Sum和C出)。
- 哪里, Cin->随身携带和C出->执行
Full Adder真值表:
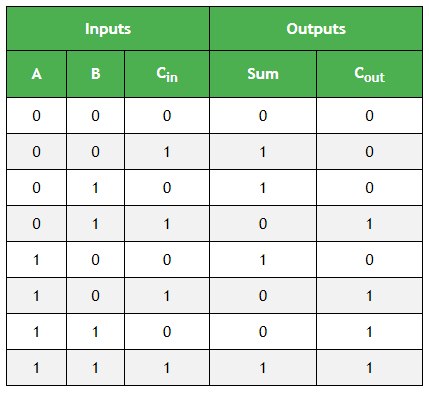
输出变量总和" S"的K-map简化:
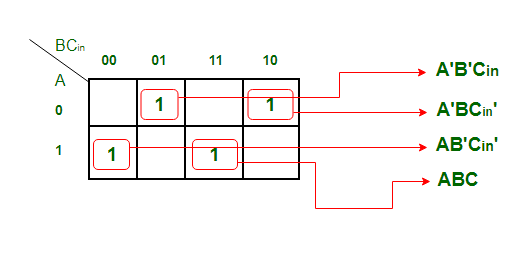
得到的方程是
S = A'B'Cin + AB'Cin' + ABC + A'BCin'该方程可以简化为
S = B'(A'Cin+ACin') + B(AC + A'Cin')
S = B'(A xor Cin) + B (A xor Cin)'
S = A xor B xor Cin输出变量" C"的K-map简化出‘
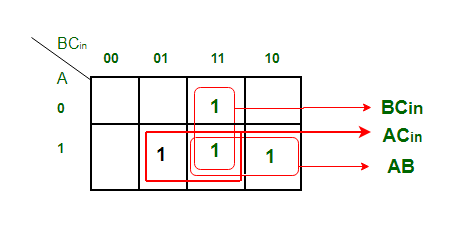
得到的方程是
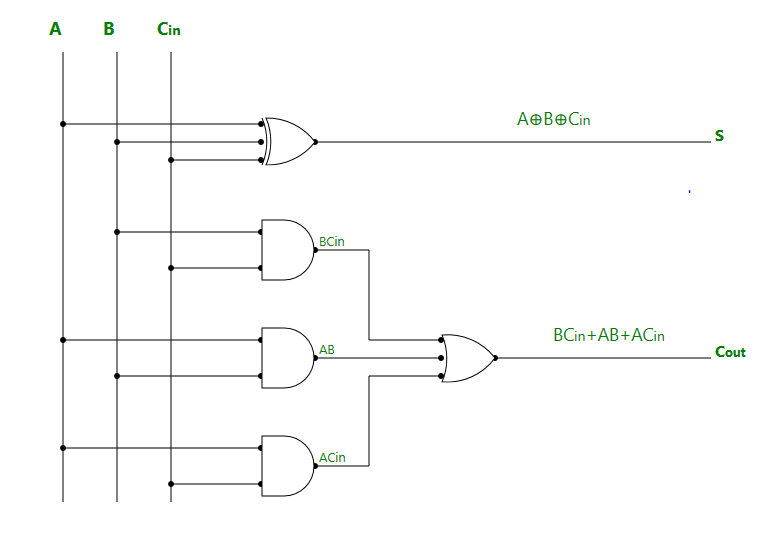
Cout = BCin + AB + ACin全加器逻辑图:
3.半减法器:
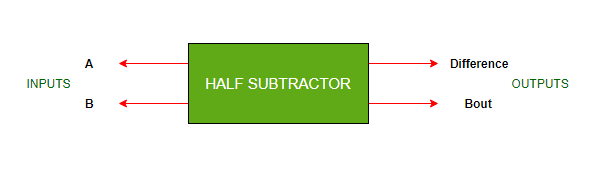
- 它是一种组合逻辑电路, 设计用于对两个单个位进行减法运算。
- 它包含两个输入(A和B), 并产生两个输出(差和借位输出)。
半减法器真值表:
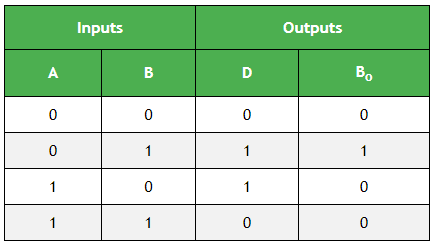
输出变量" D"的K-map简化:
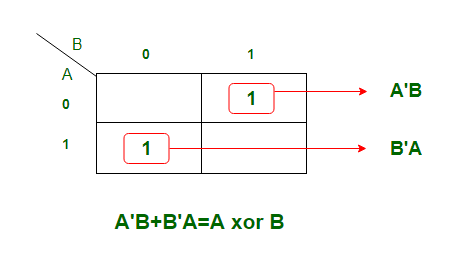
得到的方程是
D = A'B + AB'在逻辑上可以写成
D = A xor B输出变量" B"的K-map简化出‘:
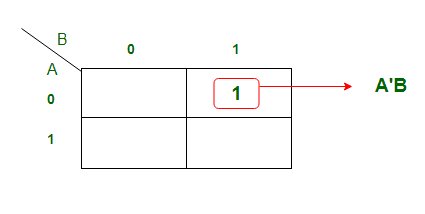
从上面的K-map得到的方程是
Bout = A'B半减法器的逻辑图:
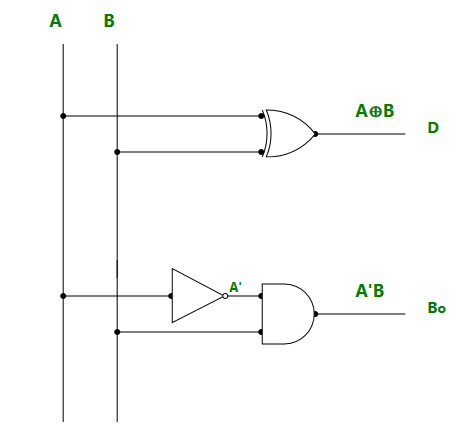
4.全减法器:
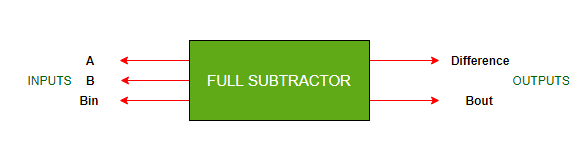
- 它是一种组合逻辑电路, 旨在执行三个单位的减法。
- 它包含三个输入(A, B, Bin)并产生两个输出(D, B出)。
- 其中, A和B称为u和换位位。
- 而且, Bin->借入和B出->借用
完全减法器的真值表:
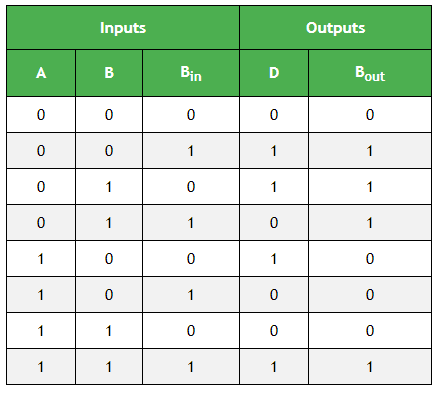
输出变量" D"的K-map简化:
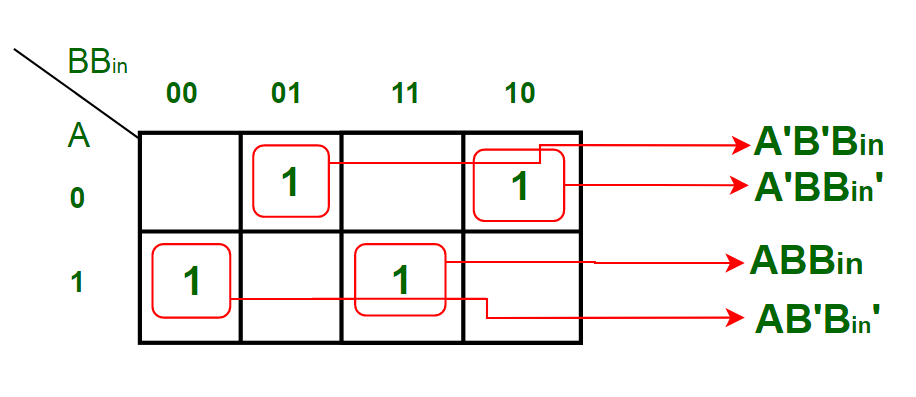
从上面的K-map得到的方程是
D = A'B'Bin + AB'Bin' + ABBin + A'BBin'可以简化为
D = B'(A'Bin + ABin') + B(ABin + A'Bin')
D = B'(A xor Bin) + B(A xor Bin)'
D = A xor B xor Bin输出变量" B"的K-map简化出‘:
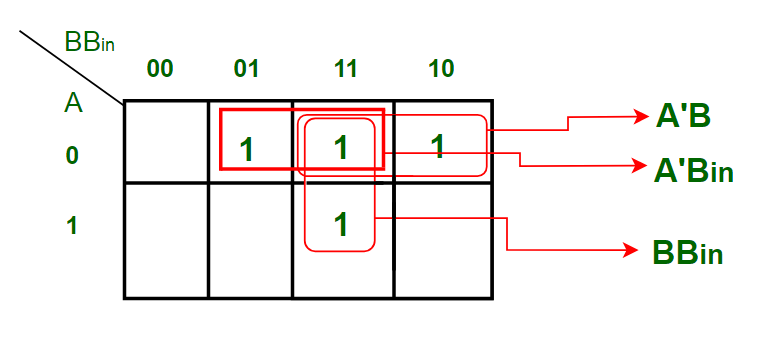
得到的方程是
Bout = BBin + A'B + A'Bin完全减法器的逻辑图:
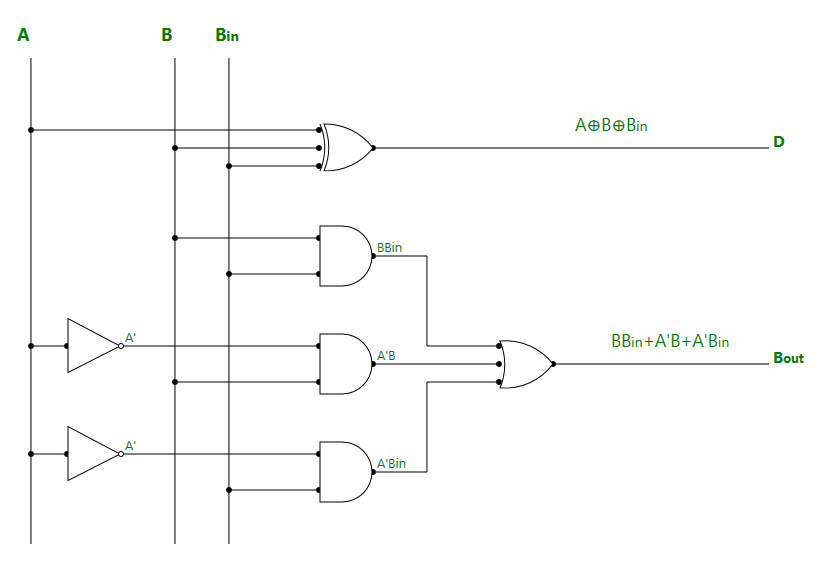
应用范围:
- 用于在电子计算器和其他数字设备中执行算术计算。
- 在计时器和程序计数器中。
- 在数字信号处理中很有用。

