LCM和HCF详细介绍

因子和倍数：所有将一个数字完全除, 即不留下任何余数的数字, 称为该因子。例如, 24可以被1、2、3、4、6、8、12、24完全整除。这些数字中的每一个被称为因子24, 而24被称为这些数字中的每一个的倍数。

LCM：每个给定数字可精确整除的最小数字称为这些数字的最小公倍数。例如, 考虑数字3、31和62(2 x 31)。这些数字的LCM为2 x 3 x 31 = 186。

为了找到给定数字的LCM, 我们将每个数字表示为质数的乘积。出现在任何数字的素数分解中的素数的乘积最高幂为我们提供了LCM。

例如, 考虑数字2、3、4(2 x 2), 5、6(2 x 3)。这些数字的LCM为2 x 2 x 3 x 5 =60。2的最高幂来自4的素因数分解, 3的最高幂来自3的素因数分解和6的素数分解, 以及5的最高幂来自5的素因数分解。

HCF：将两个或多个数字相除的最大数字是这些数字的最高公因子(HCF)。例如, 考虑数字30(2 x 3 x 5), 36(2 x 2 x 3 x 3), 42(2 x 3 x 7), 45(3 x 3 x 5)。 3是将这些数字除以最大的数字, 因此是这些数字的HCF。

HCF也称为最大公约数(GCD)。

要查找两个或多个数字的HCF, 请将每个数字表示为质数的乘积。普通素数的最小幂乘积使我们得到了HCF。这是我们在上面的步骤中说明的方法。

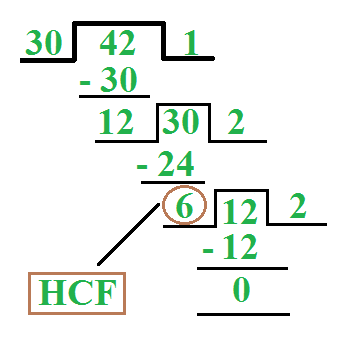
同样, 为了找到两个数的HCF, 我们也可以采用长除法进行。我们将较大的数字除以较小的数字(除数)。现在, 我们将除数除以上一阶段获得的余数。我们重复相同的过程, 直到剩下的零。在那个阶段, 最后的除数将是所需的HCF。

例如, 我们发现HCF为30和42。

对于两个数字" a"和" b", LCM x HCF = a x b

互素的HCF = 1

对于两个分数,

HCF = HCF(分子)/ LCM(分母)

LCM = LCM(分子)/ HCF(分母)

大于1的自然数总是可以写成两个自然数的最大公除数(gcd)和最小公倍数(lcm)之和。

x = gcd(a, b)+ lcm(a, b)。

让我们证明一下。令x为任何大于1的自然数, 并且a和b也是两个自然数(大于或等于1)。

让我们来

a = x-1和b = 1

现在我们找到a和b的lcm,

lcm(a, b)= a —-1

这仅仅是因为任何1的自然数的lcm就是数字本身。

现在我们找到a和b的gcd

gcd(a, b)= 1 --2

因为任何自然数为1的gcd都是1, 因为1是两个数的最高公因数。

将等式1和2相加得到

lcm(a, b)+ gcd(a, b)= a + 1

放置a和b的值

lcm(a, b)+ gcd(a, b)= x-1 + 1

lcm(a, b)+ gcd(a, b)= x

样本问题

问题1：两个数字的比例为5:11。如果他们的HCF为7, 则找到数字。

解决方案：设数字为5m和11m。由于5:11已经是降低的比例, 因此" m"必须是HCF。因此, 数字为5 x 7 = 35和11 x 7 = 77。

问题2 ：找到木板的长度, 该木板可用于在最短时间内准确测量4 m 50 cm, 9 m 90 cm和16 m 20 cm的长度。

解决方案：让我们首先将每个长度转换为厘米。因此, 长度分别为450厘米, 990厘米和1620厘米。现在, 我们需要找到可用于测量这些长度的最大木板的长度, 因为最大木板将花费最少的时间。为此, 我们需要采用450、990和1620的HCF。

450 = 2 x 3 x 3 x 5 x 5 = 2 x 3^2 x 5^2

990 = 2 x 3 x 3 x 5 x 11 = 2 x 3^2 x 5 x 11

1620 = 2 x 2 x 3 x 3 x 3 x 3 x 5 = 2^2 x 3^4 x 5

因此, HCF(450、990、1620)= 2 x 3 x 3 x 5 = 90

因此, 我们需要一块90厘米长的木板来在最短的时间内测量给定的长度。

问题3：求出最大数, 该数除以70和50分别剩下余数1和4。

解决方案：所需数目分别将余数1和4分别除以70和50。这意味着数字正好除以69和46。

因此, 我们需要找到69(3 x 23)和46(2 x 23)的HCF。

HCF(69, 46)= 23

因此, 23是必需的数字。

问题4：在每种情况下, 找出将64、136和238相除的最大数, 以保留相同的余数。

解决方案：为了找到所需的数字, 我们需要找到(136-64), (238-136)和(238-64)的HCF, 即HCF(72、102、174)。

72 = 2^3 x 3^2

102 = 2 x 3 x 17

174 = 2 x 3 x 29

因此, HCF(72, 102, 174)= 2 x 3 = 6

因此, 6是必需的数字。

问题5：求出分别除以5, 7, 9和12的最小数, 在每种情况下剩下相同的余数3

解决方案：在这些类型的问题中, 我们需要找到除数的LCM并在其中添加公共余数(3)。

因此, LCM(5, 7, 9, 12)= 1260

因此, 所需数字= 1260 + 3 = 1263

问题6：找到最大的四位数可以被15、21和28整除的数字。

解决方案：最大的四位数是9999。

现在, LCM(15, 21, 28)= 420

将9999除以420, 得到339。

因此, 所需的数字是9999-339 = 9660

问题7：在地面上三个不同地方的警察分别每42秒, 60秒和78秒吹一次哨子。如果他们在9:30:00时同时吹口哨, 那么他们什么时候又一起吹口哨？

解决方案：在等于其各自吹哨周期的LCM的间隔之后, 他们都会同时再次吹哨。

因此, LCM(42、60、78)= 2 x 3 x 7 x 10 x 13 = 5460

因此, 他们将在5460秒后(即1小时31分钟后, 即11:01:00小时)再次同时吹哨。

问题8：找出最小的数, 该数在除以6, 7, 8时将剩下余数3, 但在除以9时不留下余数。

解决方案：LCM(6, 7, 8)= 168

因此, 数字的形式为168m + 3。

现在, 168m + 3应该可以被9整除。

我们知道, 如果数字的总和是9的倍数, 那么它可以被9整除。

对于m = 1, 数字是168 + 3 = 171, 其数字之和是9。

因此, 所需的数字是171。

问题9：两个数字的比例为2：3。如果它们的LCM和HCF的乘积为294, 请找到数字。

解决方案：假设共同比率为" m"。因此, 数字为2m和3m。

现在, 我们知道数字乘积= LCM和HCF的乘积。

=> 2m x 3m = 294

=>m^2= 49

=>m= 7

因此, 数字是14和21。

问题10：尺寸为180m x 105m的矩形区域应由相同的正方形瓷砖铺成。查找每个图块的大小和所需的图块数。

解决方案：我们需要找到正方形瓷砖的大小, 以使许多瓷砖精确地覆盖该区域, 而不会留下未铺砌的区域。

为此, 我们找到了字段长度和宽度的HCF。

HCF(180, 105)= 15

因此, 每个图块的大小= 15m x 15m

此外, 图块数=区域面积/每个图块的面积

=>瓦片数=(180 x 105)/(15 x 15)

=>瓦片数= 84

因此, 我们需要84个瓦片, 每个瓦片的大小为15m x 15m。

问题11：将3块面积为60m^2、84 m^2、108 m^2的长方形场地划分为相同的长方形花坛，每个花坛长6 m。找出每个花坛的宽度。

解决方案：

我们需要将每个大字段分成较小的花床, 以使每个花床的面积相同。

因此, 我们找到了较大字段的HCF, 这给了我们较小字段的面积。

HCF(60、84、108)= 12

现在, 这个HCF是面积(以m^2为单位)每个花坛。

另外, 矩形区域的面积=长度x宽度

=> 12 = 6 x宽度

=>宽度= 2 m

因此, 每个花床将为2 m宽。

问题12：找到最大的学生人数, 其中可以分配182个巧克力和247个糖果, 以使每个学生获得的人数相同。另外, 找到每个学生将获得的巧克力和糖果的数量。

解决方案: 我们需要找到可用的巧克力和糖果数量的HCF, 这将使我们的学生人数增加。

HCF(182, 247)= 13

因此, 可以有13个学生。

此外, 每位学生的巧克力数量= 182/13 = 14

每个学生的太妃糖数量= 247/13 = 19

HCF和LCM问题S2

LCM程序

• 查找两个数字的LCM的程序
• 给定数组元素的LCM
• 在不使用GCD的情况下查找两个以上(或数组)数字的LCM
• 无需使用GCD即可查找2个数字的LCM的程序
• 检查数组元素的LCM是否可被质数整除
• 查找有理数的LCM
• 给定数字的数字的LCM
• 数组元素的LCM的主要因素
• LCM为N的最大非重复数之和

HCF计划

• 程序以迭代方式查找HCF
• 查找2个数字的HCF(最高公因子)的程序
• 查找两个数字的GCD或HCF的程序
• 给定LCM和HCF时查找其他数字
• 分数(或有理数)数组的HCF

LCM测验

如果你对以上讨论的主题有任何疑问, 或者在任何问题上都遇到困难, 或者你想讨论除上述问题之外的其他问题, 请写评论。

如果发现任何不正确的地方, 或者想分享有关上述主题的更多信息, 请写评论。