本文概述
问题陈述:考虑一行n个硬币, 值v1。 。 。 vn, 其中n为偶数。我们交替轮流与对手进行比赛。在每个回合中, 玩家从该行中选择第一个或最后一个硬币, 将其从行中永久删除, 然后接收硬币的价值。确定如果我们先走, 我们绝对可以赢得的最大金额。
注意:对手和用户一样聪明。
让我们用几个例子来了解问题:
1. 5、3、7、10:用户收集的最大值为15(10 + 5)
2. 8、15、3、7:用户收集的最大值为22(7 + 15)
在每一步中选择最佳方案是否能提供最佳解决方案?
否。在第二个示例中, 这是游戏的完成方式:
1.
......用户选择8。
......对手选择15。
......用户选择7。
......对手选择3。
用户收集的总价值为15(8 + 7)
2.
......用户选择7。
......对手选择8。
......用户选择15。
......对手选择3。
用户收集的总价值为22(7 + 15)
我们已经讨论了一种进行4次递归调用的方法。在这篇文章中,我们讨论了一种新的方法,它进行了两次递归调用。
有两种选择:
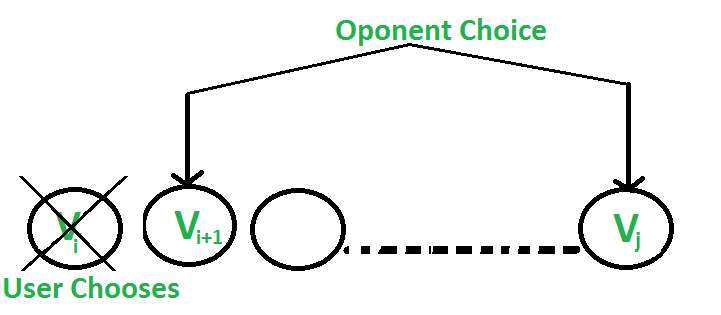
1. 用户选择值为Vi的第i个硬币:对手选择第(i + 1)个硬币或第j个硬币。对手打算选择硬币给用户留下最小的价值。
即, 用户可以收集值Vi +(Sum – Vi)– F(i + 1, j, Sum – Vi), 其中Sum是从索引i到j的硬币总和。表达式可以简化为Sum – F(i + 1, j, Sum – Vi)
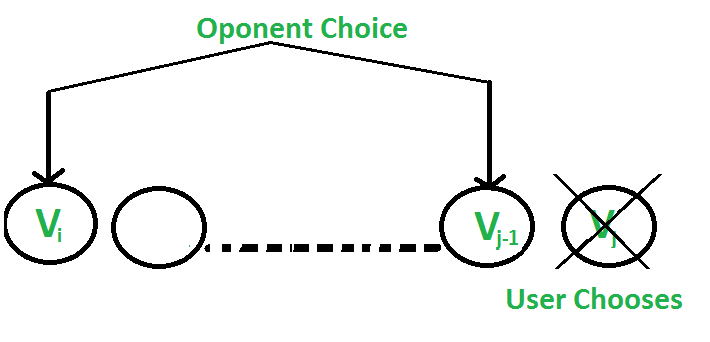
2. 用户选择值Vj的第j个硬币:对手选择第i个硬币或第(j-1)个硬币。对手打算选择硬币给用户留下最小的价值。
即, 用户可以收集值Vj +(Sum – Vj)– F(i, j-1, Sum – Vj), 其中Sum是从索引i到j的硬币之和。该表达式可以简化为Sum – F(i, j-1, Sum – Vj)
以下是基于以上两个选择的递归解决方案。我们最多选择两个。
F(i, j) represents the maximum value the user can collect from
i'th coin to j'th coin.
arr[] represents the list of coins
F(i, j) = Max(Sum - F(i+1, j, Sum-arr[i]), Sum - F(i, j-1, Sum-arr[j]))
Base Case
F(i, j) = max(arr[i], arr[j]) If j == i+1简单的递归解决方案
CPP
// C++ program to find out maximum value from a
// given sequence of coins
#include <bits/stdc++.h>
using namespace std;
int oSRec( int arr[], int i, int j, int sum)
{
if (j == i + 1)
return max(arr[i], arr[j]);
// For both of your choices, the opponent
// gives you total sum minus maximum of
// his value
return max((sum - oSRec(arr, i + 1, j, sum - arr[i])), (sum - oSRec(arr, i, j - 1, sum - arr[j])));
}
// Returns optimal value possible that a player can
// collect from an array of coins of size n. Note
// than n must be even
int optimalStrategyOfGame( int * arr, int n)
{
int sum = 0;
sum = accumulate(arr, arr + n, sum);
return oSRec(arr, 0, n - 1, sum);
}
// Driver program to test above function
int main()
{
int arr1[] = { 8, 15, 3, 7 };
int n = sizeof (arr1) / sizeof (arr1[0]);
printf ( "%d\n" , optimalStrategyOfGame(arr1, n));
int arr2[] = { 2, 2, 2, 2 };
n = sizeof (arr2) / sizeof (arr2[0]);
printf ( "%d\n" , optimalStrategyOfGame(arr2, n));
int arr3[] = { 20, 30, 2, 2, 2, 10 };
n = sizeof (arr3) / sizeof (arr3[0]);
printf ( "%d\n" , optimalStrategyOfGame(arr3, n));
return 0;
}Java
// Java program to find out maximum value from a
// given sequence of coins
import java .io.*;
class GFG
{
static int oSRec( int []arr, int i, int j, int sum)
{
if (j == i + 1 )
return Math.max(arr[i], arr[j]);
// For both of your choices, the opponent
// gives you total sum minus maximum of
// his value
return Math.max((sum - oSRec(arr, i + 1 , j, sum - arr[i])), (sum - oSRec(arr, i, j - 1 , sum - arr[j])));
}
// Returns optimal value possible that a player can
// collect from an array of coins of size n. Note
// than n must be even
static int optimalStrategyOfGame( int [] arr, int n)
{
int sum = 0 ;
for ( int i = 0 ; i < n; i++)
{
sum += arr[i];
}
return oSRec(arr, 0 , n - 1 , sum);
}
// Driver code
static public void main (String[] args)
{
int []arr1 = { 8 , 15 , 3 , 7 };
int n = arr1.length;
System.out.println(optimalStrategyOfGame(arr1, n));
int []arr2 = { 2 , 2 , 2 , 2 };
n = arr2.length;
System.out.println(optimalStrategyOfGame(arr2, n));
int []arr3 = { 20 , 30 , 2 , 2 , 2 , 10 };
n = arr3.length ;
System.out.println(optimalStrategyOfGame(arr3, n));
}
}
// This code is contributed by anuj_67..python
# python program to find out maximum value from a
# given sequence of coins
def oSRec (arr, i, j, Sum ):
if (j = = i + 1 ):
return max (arr[i], arr[j])
# For both of your choices, the opponent
# gives you total Sum minus maximum of
# his value
return max (( Sum - oSRec(arr, i + 1 , j, Sum - arr[i])), ( Sum - oSRec(arr, i, j - 1 , Sum - arr[j])))
# Returns optimal value possible that a player can
# collect from an array of coins of size n. Note
# than n must be even
def optimalStrategyOfGame(arr, n):
Sum = 0
Sum = sum (arr)
return oSRec(arr, 0 , n - 1 , Sum )
# Driver code
arr1 = [ 8 , 15 , 3 , 7 ]
n = len (arr1)
print (optimalStrategyOfGame(arr1, n))
arr2 = [ 2 , 2 , 2 , 2 ]
n = len (arr2)
print (optimalStrategyOfGame(arr2, n))
arr3 = [ 20 , 30 , 2 , 2 , 2 , 10 ]
n = len (arr3)
print (optimalStrategyOfGame(arr3, n))
# This code is contributed by Mohit kumar 29C#
// C# program to find out maximum value from a
// given sequence of coins
using System;
class GFG
{
static int oSRec( int []arr, int i, int j, int sum)
{
if (j == i + 1)
return Math.Max(arr[i], arr[j]);
// For both of your choices, the opponent
// gives you total sum minus maximum of
// his value
return Math.Max((sum - oSRec(arr, i + 1, j, sum - arr[i])), (sum - oSRec(arr, i, j - 1, sum - arr[j])));
}
// Returns optimal value possible that a player can
// collect from an array of coins of size n. Note
// than n must be even
static int optimalStrategyOfGame( int [] arr, int n)
{
int sum = 0;
for ( int i = 0; i < n; i++)
{
sum += arr[i];
}
return oSRec(arr, 0, n - 1, sum);
}
// Driver code
static public void Main ()
{
int []arr1 = { 8, 15, 3, 7 };
int n = arr1.Length;
Console.WriteLine(optimalStrategyOfGame(arr1, n));
int []arr2 = { 2, 2, 2, 2 };
n = arr2.Length;
Console.WriteLine(optimalStrategyOfGame(arr2, n));
int []arr3 = { 20, 30, 2, 2, 2, 10 };
n = arr3.Length;
Console.WriteLine(optimalStrategyOfGame(arr3, n));
}
}
// This code is contributed by AnkitRai01输出如下:
22
4
42基于内存的解决方案
CPP
// C++ program to find out maximum value from a
// given sequence of coins
#include <bits/stdc++.h>
using namespace std;
const int MAX = 100;
int memo[MAX][MAX];
int oSRec( int arr[], int i, int j, int sum)
{
if (j == i + 1)
return max(arr[i], arr[j]);
if (memo[i][j] != -1)
return memo[i][j];
// For both of your choices, the opponent
// gives you total sum minus maximum of
// his value
memo[i][j] = max((sum - oSRec(arr, i + 1, j, sum - arr[i])), (sum - oSRec(arr, i, j - 1, sum - arr[j])));
return memo[i][j];
}
// Returns optimal value possible that a player can
// collect from an array of coins of size n. Note
// than n must be even
int optimalStrategyOfGame( int * arr, int n)
{
// Compute sum of elements
int sum = 0;
sum = accumulate(arr, arr + n, sum);
// Initialize memoization table
memset (memo, -1, sizeof (memo));
return oSRec(arr, 0, n - 1, sum);
}
// Driver program to test above function
int main()
{
int arr1[] = { 8, 15, 3, 7 };
int n = sizeof (arr1) / sizeof (arr1[0]);
printf ( "%d\n" , optimalStrategyOfGame(arr1, n));
int arr2[] = { 2, 2, 2, 2 };
n = sizeof (arr2) / sizeof (arr2[0]);
printf ( "%d\n" , optimalStrategyOfGame(arr2, n));
int arr3[] = { 20, 30, 2, 2, 2, 10 };
n = sizeof (arr3) / sizeof (arr3[0]);
printf ( "%d\n" , optimalStrategyOfGame(arr3, n));
return 0;
}Java
// Java program to find out maximum value from a
// given sequence of coins
import java.util.*;
class GFG{
static int MAX = 100 ;
static int [][]memo = new int [MAX][MAX];
static int oSRec( int arr[], int i, int j, int sum)
{
if (j == i + 1 )
return Math.max(arr[i], arr[j]);
if (memo[i][j] != - 1 )
return memo[i][j];
// For both of your choices, the opponent
// gives you total sum minus maximum of
// his value
memo[i][j] = Math.max((sum - oSRec(arr, i + 1 , j, sum - arr[i])), (sum - oSRec(arr, i, j - 1 , sum - arr[j])));
return memo[i][j];
}
static int accumulate( int [] arr, int start, int end)
{
int sum= 0 ;
for ( int i= 0 ; i < arr.length; i++)
sum += arr[i];
return sum;
}
// Returns optimal value possible that a player can
// collect from an array of coins of size n. Note
// than n must be even
static int optimalStrategyOfGame( int []arr, int n)
{
// Compute sum of elements
int sum = 0 ;
sum = accumulate(arr, 0 , n);
// Initialize memoization table
for ( int j = 0 ; j < MAX; j++)
{
for ( int k = 0 ; k < MAX; k++)
memo[j][k] = - 1 ;
}
return oSRec(arr, 0 , n - 1 , sum);
}
// Driver Code
public static void main(String[] args)
{
int arr1[] = { 8 , 15 , 3 , 7 };
int n = arr1.length;
System.out.printf( "%d\n" , optimalStrategyOfGame(arr1, n));
int arr2[] = { 2 , 2 , 2 , 2 };
n = arr2.length;
System.out.printf( "%d\n" , optimalStrategyOfGame(arr2, n));
int arr3[] = { 20 , 30 , 2 , 2 , 2 , 10 };
n = arr3.length;
System.out.printf( "%d\n" , optimalStrategyOfGame(arr3, n));
}
}
// This code is contributed by gauravrajput1C#
// C# program to find out maximum value from a
// given sequence of coins
using System;
class GFG{
static int MAX = 100;
static int [, ] memo = new int [MAX, MAX];
static int oSRec( int []arr, int i, int j, int sum)
{
if (j == i + 1)
return Math.Max(arr[i], arr[j]);
if (memo[i, j] != -1)
return memo[i, j];
// For both of your choices, the opponent
// gives you total sum minus maximum of
// his value
memo[i, j] = Math.Max((sum - oSRec(arr, i + 1, j, sum - arr[i])), (sum - oSRec(arr, i, j - 1, sum - arr[j])));
return memo[i, j];
}
static int accumulate( int [] arr, int start, int end)
{
int sum = 0;
for ( int i = 0; i < arr.Length; i++)
sum += arr[i];
return sum;
}
// Returns optimal value possible that a player can
// collect from an array of coins of size n. Note
// than n must be even
static int optimalStrategyOfGame( int [] arr, int n)
{
// Compute sum of elements
int sum = 0;
sum = accumulate(arr, 0, n);
// Initialize memoization table
for ( int j = 0; j < MAX; j++)
{
for ( int k = 0; k < MAX; k++)
memo[j, k] = -1;
}
return oSRec(arr, 0, n - 1, sum);
}
// Driver Code
public static void Main(String[] args)
{
int []arr1 = { 8, 15, 3, 7 };
int n = arr1.Length;
Console.Write( "{0}\n" , optimalStrategyOfGame(arr1, n));
int []arr2 = { 2, 2, 2, 2 };
n = arr2.Length;
Console.Write( "{0}\n" , optimalStrategyOfGame(arr2, n));
int []arr3 = { 20, 30, 2, 2, 2, 10 };
n = arr3.Length;
Console.Write( "{0}\n" , optimalStrategyOfGame(arr3, n));
}
}
// This code is contributed by Rohit_ranjan输出如下:
22
4
42
![从字法上最小长度N的排列,使得对于正好为K个索引,a[i] a[i]+1](https://www.lsbin.com/wp-content/themes/begin%20lts/img/loading.png)