算法设计：瓷砖问题介绍和解决方案

给定一块" 2 x n"板和尺寸为" 2 x 1"的砖块, 计算使用2 x 1砖块对给定板块进行铺砖的方法数量。瓷砖可以水平放置(即1 x 2瓷砖)或垂直放置(例如2 x 1瓷砖)。

例子：

Input n = 3
Output: 3
Explanation:
We need 3 tiles to tile the board of size  2 x 3. 
We can tile the board using following ways
1) Place all 3 tiles vertically. 
2) Place first tile vertically and remaining 2 tiles horizontally.
3) Place first 2 tiles horizontally and remaining tiles vertically

Input n = 4
Output: 5
Explanation:
For a 2 x 4 board, there are 5 ways
1) All 4 vertical
2) All 4 horizontal
3) First 2 vertical, remaining 2 horizontal
4) First 2 horizontal, remaining 2 vertical
5) Corner 2 vertical, middle 2 horizontal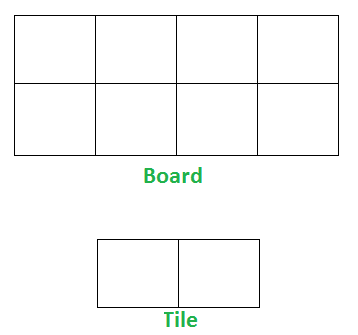

假设" count(n)"是在" 2 x n"网格上放置图块的方式的计数, 我们有以下两种方法来放置第一个图块。

1)如果我们垂直放置第一个图块, 则问题将减少为" count(n-1)"

2)如果我们将第一个图块水平放置, 则必须也将第二个图块也水平放置。因此问题减少到" count(n-2)"

因此, count(n)可以编写如下。

count(n) = n if n = 1 or n = 2
   count(n) = count(n-1) + count(n-2)

上面的重复不过是斐波那契数表达。我们可以在O(Log n)时间中找到第n个斐波那契数, 有关找到第n个斐波那契数的所有方法, 请参见下文。

第n个斐波那契数的不同方法.

计算使用1 x m尺寸的瓷砖来铺平n x m的地板的方法数量

本文由Saurabh Jain提供。如果发现任何不正确的地方, 或者想分享有关上述主题的更多信息, 请发表评论。