先决条件– 数字系统和基本转换
Excess-3二进制码是一种无加权自互补BCD码。
自我补全属性表示Excess-3的1的补码是相应十进制数字的9的补码的超出3的代码。此属性很有用, 因为十进制数可以像补码一样容易地补成9(用于减法)。只需反转所有位即可。
例如, 3(0011)的多余3代码为0110, 要找到3的补码的多余3代码, 我们只需要找到0的1的补码-> 1001, 这也是多余3 9的3的补码->(9-3)= 6。
将BCD(8421)转换为Excess-3 –
顾名思义, 只要将BCD数字加3, 就可以将其转换为相应的Excess-3代码。
让
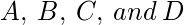
是代表二进制数的位, 其中
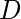
是LSB,
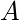
是MSB, 并且
让
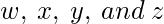
是表示二进制数字格雷码的位, 其中
是LSB,
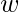
是MSB。
转换的真值表如下所示。 X标记不在乎条件。

为了找到相应的数字电路, 我们将对每个Excess-3代码位使用K-Map技术作为输出, 而将BCD编号的所有位用作输入。
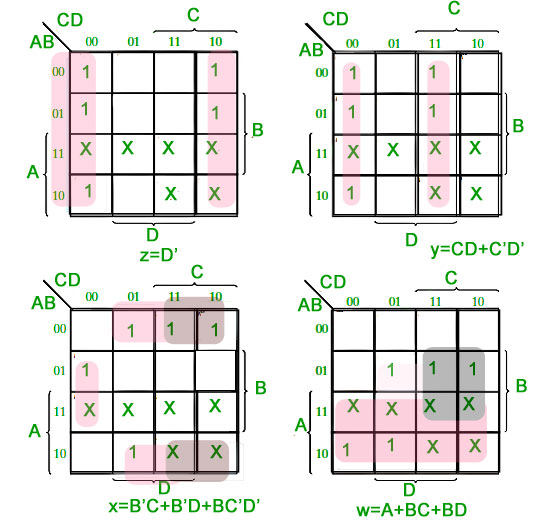
对应于Excess-3码位的最小化布尔表达式–
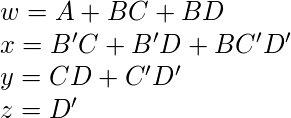
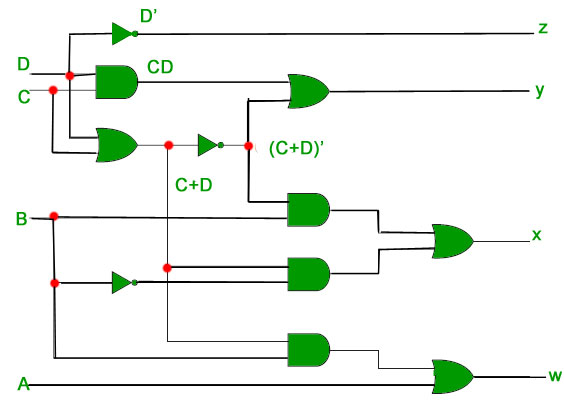
对应的数字电路-
将Excess-3转换为BCD(8421)–
Excess-3码可以以相同的方式转换回BCD。
让
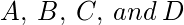
是代表二进制数的位, 其中
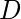
是LSB,
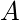
是MSB, 并且
让
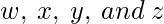
是表示二进制数字格雷码的位, 其中
是LSB,
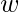
是MSB。
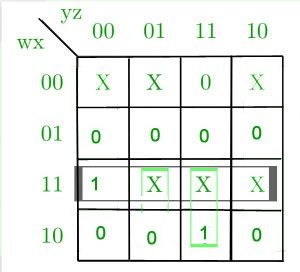
转换的真值表如下所示。 X标记不在乎条件。

D-的K-Map
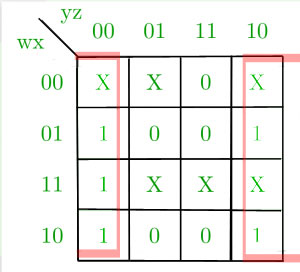
K-Map for C-
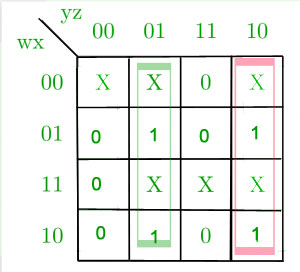
B-的K-Map
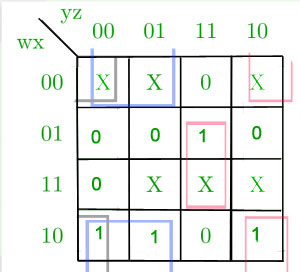
K-Map for A-
<img src ="
Excess-3码位的对应的最小化布尔表达式–
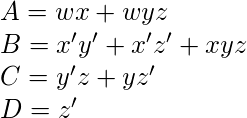
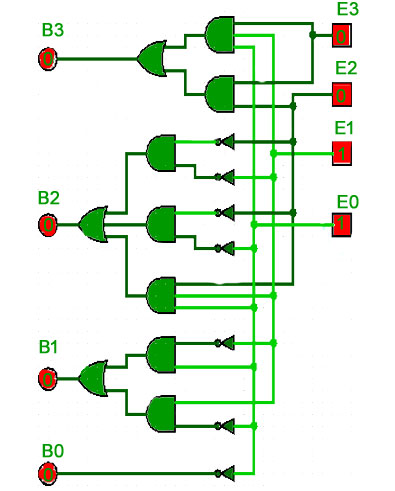
相应的数字电路–
这里
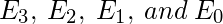
相当于
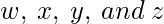
和
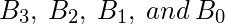
相当于
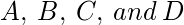
.
参考资料
数字设计, 莫里斯·玛诺和迈克尔·西莱蒂的第5版
Excess-3 –维基百科:https://en.wikipedia.org/wiki/Excess-3
如果发现任何不正确的地方, 或者想分享有关上述主题的更多信息, 请写评论。

