斐波那契堆介绍和实现原理分析|S1

堆主要用于实现优先级队列。我们在以前的文章中讨论了以下内容。

二叉堆(Binary Heap)

二项堆(Binomial Heap)

在时间复杂度方面, 斐波那契堆击败了二叉堆和二项堆。

下面是斐波那契堆的平摊时间复杂度。

1) Find Min:      Θ(1)     [Same as both Binary and Binomial]
2) Delete Min:    O(Log n) [Θ(Log n) in both Binary and Binomial]
3) Insert:        Θ(1)     [Θ(Log n) in Binary and Θ(1) in Binomial]
4) Decrease-Key:  Θ(1)     [Θ(Log n) in both Binary and Binomial]
5) Merge:         Θ(1)     [Θ(m Log n) or Θ(m+n) in Binary and
                            Θ(Log n) in Binomial]

像二项堆一样，斐波那契堆是具有最小堆或最大堆属性的树的集合。在斐波那契堆中，树可以有任何形状，甚至所有树都可以是单个节点(这与二项堆不同，二项堆中每棵树都必须是二项树)。

以下是斐波那契堆取自这里(https://www.cs.princeton.edu/~wayne/teaching/fibonacci-heap.pdf).

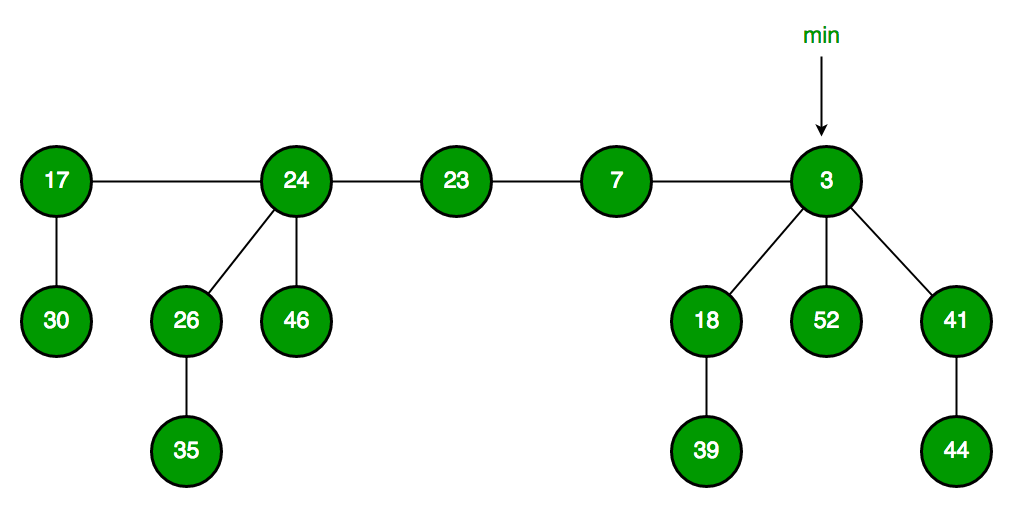
斐波那契堆保持指向最小值(它是树的根)的指针。所有树的根都使用圆形双向链表进行连接, 因此可以使用单个" min"指针访问它们。

主要思想是以"惰性"方式执行操作。例如, 合并操作仅链接两个堆, 插入操作仅添加具有单个节点的新树。最小的操作提取是最复杂的操作。它确实延迟了合并树木的工作。这使删除操作也变得很复杂, 因为删除操作首先将键减小到负无穷大, 然后再调用提取最小。

以下是有关斐波那契堆的一些有趣事实

1. 减小键的时间复杂度在Dijkstra和Prim算法中很重要。使用二叉堆, 这些算法的时间复杂度为O(VLogV + ELogV)。如果使用斐波那契堆, 那么时间复杂度将提高到O(VLogV + E)
2. 尽管斐波那契堆在时间复杂度方面看起来很有希望, 但由于隐藏常数很高, 因此在实践中发现它很慢(来源维基)。
3. 之所以称呼Fibonacci堆, 是因为在运行时间分析中使用了Fibonacci数。而且, 斐波那契堆中的每个节点的度数最多为O(log n), 并且以k度数的节点为根的子树的大小至少为Fk + 2, 其中Fķ是第k个斐波那契数。

我们很快将详细讨论斐波那契堆操作。

如果发现任何不正确的地方, 或者想分享有关上述主题的更多信息, 请写评论。