高级数据结构：如何实现斐波那契堆–插入和联合操作？

先决条件：斐波那契堆(简介)

斐波那契堆是具有最小堆或最大堆属性的树的集合。在斐波那契堆中, 即使所有树都可以是单个节点, 树木也可以具有任何形状(这与二项式堆不同, 后者每棵树都必须是二项式树)。

在本文中, 我们将讨论斐波那契堆上的插入和联合操作。

插入：要将节点插入斐波那契堆H中, 请遵循以下算法：

创建一个新节点"x"。
检查堆H是否为空。
如果H为空, 则：使x为根列表中的唯一节点。并将H(min)指针设置为x。
否则：将x插入根列表并更新H(min)。

例子：

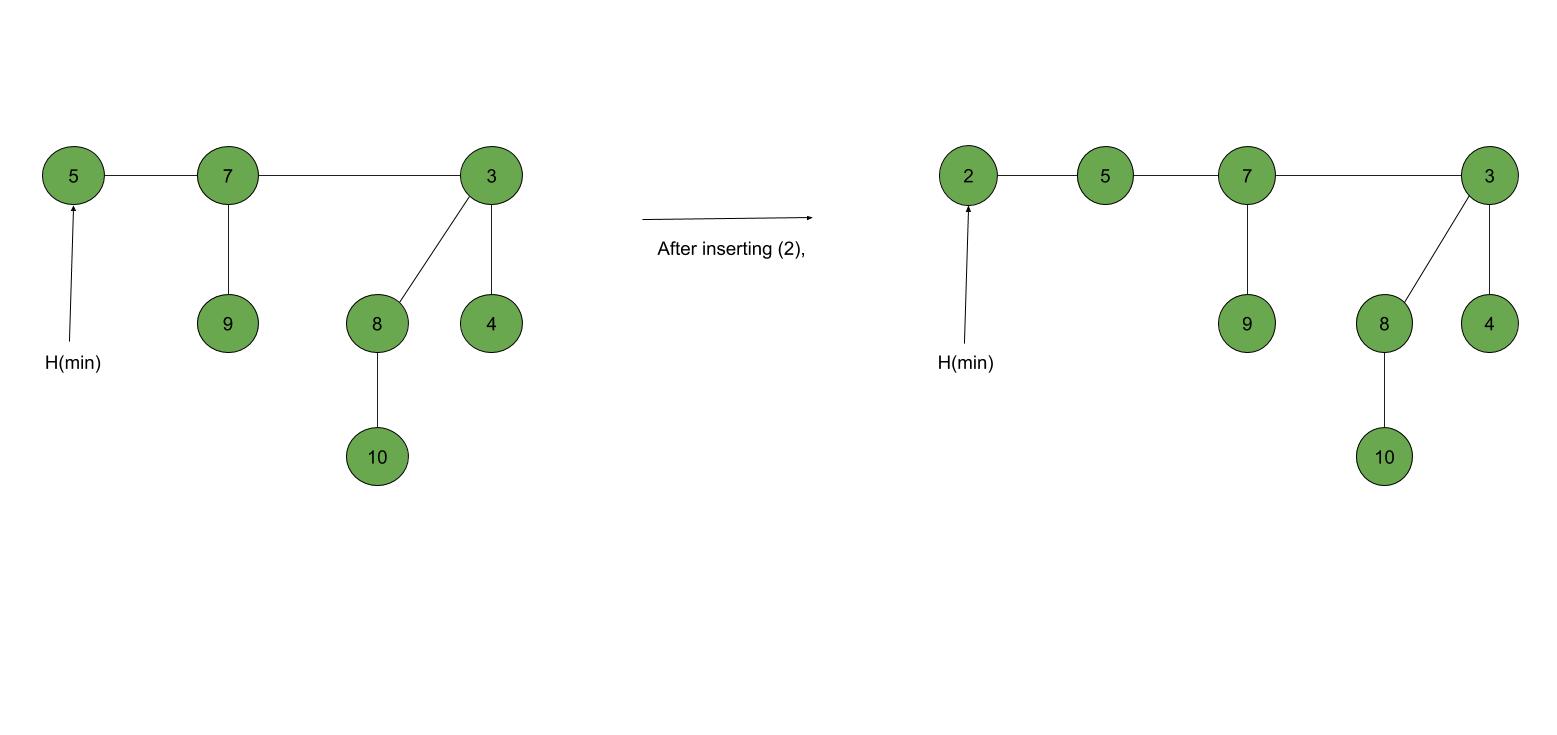
联合：两个斐波纳契堆H1和H2的并集可以按以下方式完成：

将Fibonacci堆的H1和H2的根列表联接起来, 并制作单个Fibonacci堆H。
如果H1(min)<H2(min), 则：H(min)= H1(min)。
否则：H(min)= H2(min)。

例子：

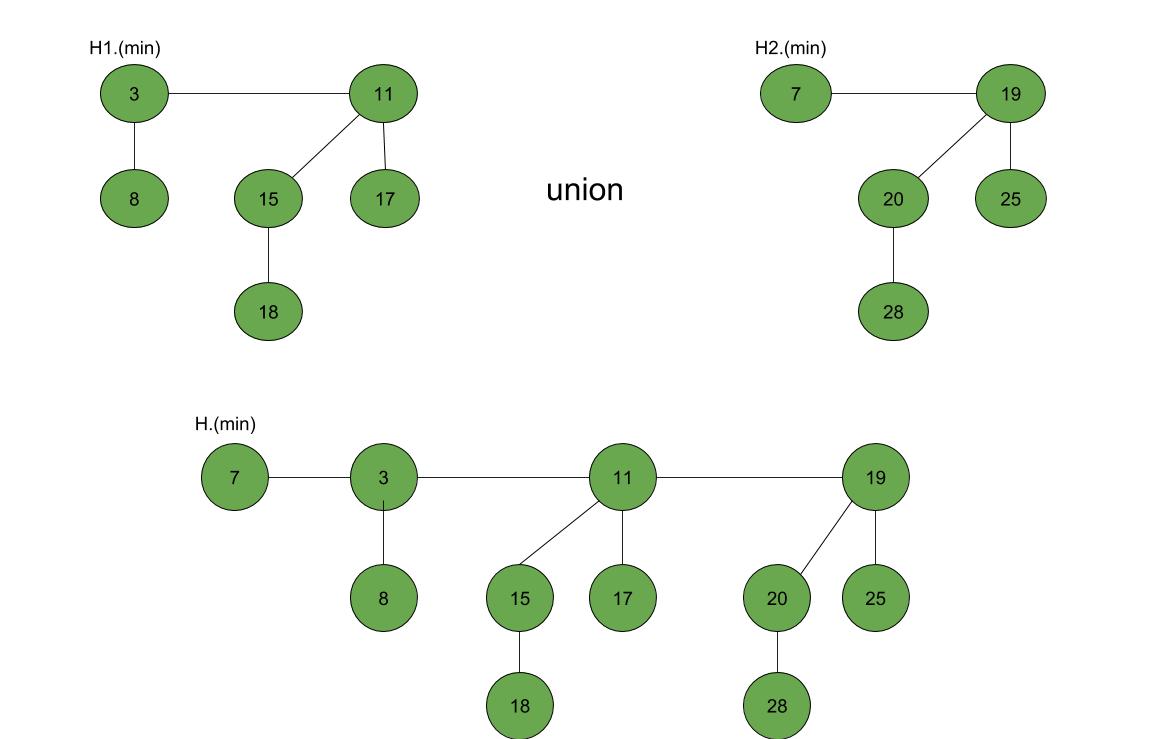
以下是演示在斐波那契堆中进行构建和插入的程序：

// C++ program to demonstrate building
// and inserting in a Fibonacci heap
#include <cstdlib>
#include <iostream>
#include <malloc.h>
using namespace std;
  
struct node {
     node* parent;
     node* child;
     node* left;
     node* right;
     int key;
};
  
// Creating min pointer as "mini"
struct node* mini = NULL;
  
// Declare an integer for number of nodes in the heap
int no_of_nodes = 0;
  
// Function to insert a node in heap
void insertion( int val)
{
     struct node* new_node = ( struct node*) malloc ( sizeof ( struct node));
     new_node->key = val;
     new_node->parent = NULL;
     new_node->child = NULL;
     new_node->left = new_node;
     new_node->right = new_node;
     if (mini != NULL) {
         (mini->left)->right = new_node;
         new_node->right = mini;
         new_node->left = mini->left;
         mini->left = new_node;
         if (new_node->key < mini->key)
             mini = new_node;
     }
     else {
         mini = new_node;
     }
}
  
// Function to display the heap
void display( struct node* mini)
{
     node* ptr = mini;
     if (ptr == NULL)
         cout << "The Heap is Empty" << endl;
  
     else {
         cout << "The root nodes of Heap are: " << endl;
         do {
             cout << ptr->key;
             ptr = ptr->right;
             if (ptr != mini) {
                 cout << "-->" ;
             }
         } while (ptr != mini && ptr->right != NULL);
         cout << endl
              << "The heap has " << no_of_nodes << " nodes" << endl;
     }
}
// Function to find min node in the heap
void find_min( struct node* mini)
{
     cout << "min of heap is: " << mini->key << endl;
}
  
  
// Driver code
int main()
{
  
     no_of_nodes = 7;
     insertion(4);
     insertion(3);
     insertion(7);
     insertion(5);
     insertion(2);
     insertion(1);
     insertion(10);
  
     display(mini);
  
     find_min(mini);
  
     return 0;
}

输出如下：

The root nodes of Heap are: 
1-->2-->3-->4-->7-->5-->10
The heap has 7 nodes
Min of heap is: 1

---