算法设计：第n个卡塔兰数算法实现

2021年3月26日17:10:40 发表评论 1,310 次浏览

本文概述

卡塔兰数是一个自然数序列，出现在许多有趣的计数问题中，如下列。

1. 计算包含n对正确匹配的圆括号的表达式的数量。对于n = 3,可能的表达式 ((())), ()(()), ()()(), (())(), (()()).

2. 计算可能有n个键的二叉搜索树的数量

3. 计算具有n + 1个叶子的完整二​​叉树的数目(如果每个顶点有两个子树或没有子树, 则有根的二叉树将是完整的)。

4. 给定数字n, 返回可以在2 x n点的圆中绘制n个和弦的方式数, 以使2个和弦不相交。

n = 0, 1, 2, 3，…的前几个卡塔兰数字是1,1,2,5,14,42,132,429,1430,4862，…

1, 1, 2, 5, 14, 14, 42, 132, 429, 1430, 4862, …

递归解

卡塔兰语数字满足以下递归公式。

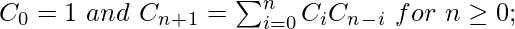
C_0 = 1 \和\ C_n _ + _ 1 = \ sum_ {i = 0} ^ {n} C_iC_n _-_ i \为\ n \ geq 0;

以下是上述递归公式的实现。

C ++

#include <iostream>
using namespace std;
 
// A recursive function to find nth catalan number
unsigned long int catalan(unsigned int n)
{
     // Base case
     if (n <= 1)
         return 1;
 
     // catalan(n) is sum of
     // catalan(i)*catalan(n-i-1)
     unsigned long int res = 0;
     for ( int i = 0; i < n; i++)
         res += catalan(i)
             * catalan(n - i - 1);
 
     return res;
}
 
// Driver code
int main()
{
     for ( int i = 0; i < 10; i++)
         cout << catalan(i) << " " ;
     return 0;
}

Java

class CatalnNumber {
 
     // A recursive function to find nth catalan number
 
     int catalan( int n)
     {
         int res = 0 ;
 
         // Base case
         if (n <= 1 )
         {
             return 1 ;
         }
         for ( int i = 0 ; i < n; i++)
         {
             res += catalan(i)
                 * catalan(n - i - 1 );
         }
         return res;
     }
 
     // Driver Code
     public static void main(String[] args)
     {
         CatalnNumber cn = new CatalnNumber();
         for ( int i = 0 ; i < 10 ; i++)
         {
             System.out.print(cn.catalan(i) + " " );
         }
     }
}

python

# A recursive function to
# find nth catalan number
def catalan(n):
     # Base Case
     if n < = 1 :
         return 1
 
     # Catalan(n) is the sum
     # of catalan(i)*catalan(n-i-1)
     res = 0
     for i in range (n):
         res + = catalan(i) * catalan(n - i - 1 )
 
     return res
 
 
# Driver Code
for i in range ( 10 ):
     print catalan(i), # This code is contributed by
# Nikhil Kumar Singh (nickzuck_007)

C#

// A recursive C# program to find
// nth catalan number
using System;
 
class GFG {
 
     // A recursive function to find
     // nth catalan number
     static int catalan( int n)
     {
         int res = 0;
 
         // Base case
         if (n <= 1)
         {
             return 1;
         }
         for ( int i = 0; i < n; i++)
         {
             res += catalan(i)
                 * catalan(n - i - 1);
         }
         return res;
     }
 
     // Driver Code
     public static void Main()
     {
         for ( int i = 0; i < 10; i++)
             Console.Write(catalan(i) + " " );
     }
}
 
// This code is contributed by
// nitin mittal.

的PHP

<?php
// PHP Program for nth
// Catalan Number
 
// A recursive function to
// find nth catalan number
function catalan( $n )
{
     
     // Base case
     if ( $n <= 1)
         return 1;
 
     // catalan(n) is sum of
     // catalan(i)*catalan(n-i-1)
     $res = 0;
     for ( $i = 0; $i < $n ; $i ++)
         $res += catalan( $i ) *
                 catalan( $n - $i - 1);
 
     return $res ;
}
 
// Driver Code
for ( $i = 0; $i < 10; $i ++)
     echo catalan( $i ), " " ;
 
// This code is contributed aj_36
?>

输出如下

1 1 2 5 14 42 132 429 1430 4862

时间复杂度上述实现的等价于第n个卡塔兰数。

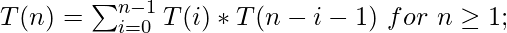
T（n）= \ sum_ {i = 0} ^ {n-1} T（i）* T（n-i-1）\表示\ n \ geq 1;

第n个卡塔兰数的值是指数的, 这使得时间复杂度是指数的。

动态编程解决方案：我们可以看到上面的递归实现做了很多重复的工作(我们可以通过绘制递归树来实现)。由于存在重叠的子问题, 我们可以为此使用动态编程。以下是基于动态编程的实现。

C ++

#include <iostream>
using namespace std;
 
// A dynamic programming based function to find nth
// Catalan number
unsigned long int catalanDP(unsigned int n)
{
     // Table to store results of subproblems
     unsigned long int catalan[n + 1];
 
     // Initialize first two values in table
     catalan[0] = catalan[1] = 1;
 
     // Fill entries in catalan[] using recursive formula
     for ( int i = 2; i <= n; i++)
     {
         catalan[i] = 0;
         for ( int j = 0; j < i; j++)
             catalan[i] += catalan[j]
                        * catalan[i - j - 1];
     }
 
     // Return last entry
     return catalan[n];
}
 
// Driver code
int main()
{
     for ( int i = 0; i < 10; i++)
         cout << catalanDP(i) << " " ;
     return 0;
}

Java

class GFG {
 
     // A dynamic programming based function to find nth
     // Catalan number
     static int catalanDP( int n)
     {
         // Table to store results of subproblems
         int catalan[] = new int [n + 2 ];
 
         // Initialize first two values in table
         catalan[ 0 ] = 1 ;
         catalan[ 1 ] = 1 ;
 
         // Fill entries in catalan[]
         // using recursive formula
         for ( int i = 2 ; i <= n; i++)
         {
             catalan[i] = 0 ;
             for ( int j = 0 ; j < i; j++)
             {
                 catalan[i]
                     += catalan[j]
                     * catalan[i - j - 1 ];
             }
         }
 
         // Return last entry
         return catalan[n];
     }
 
     // Driver code
     public static void main(String[] args)
     {
         for ( int i = 0 ; i < 10 ; i++) {
             System.out.print(catalanDP(i) + " " );
         }
     }
}
// This code contributed by Rajput-Ji

python

# A dynamic programming based function to find nth
# Catalan number
 
 
def catalan(n):
     if (n = = 0 or n = = 1 ):
         return 1
 
     # Table to store results of subproblems
     catalan = [ 0 for i in range (n + 1 )]
 
     # Initialize first two values in table
     catalan[ 0 ] = 1
     catalan[ 1 ] = 1
 
     # Fill entries in catalan[]
     # using recursive formula
     for i in range ( 2 , n + 1 ):
         catalan[i] = 0
         for j in range (i):
             catalan[i] + = catalan[j]
             catalan[i] * = catalan[i - j - 1 ]
 
     # Return last entry
     return catalan[n]
 
 
# Driver code
for i in range ( 10 ):
     print (catalan(i), end = " " )
# This code is contributed by Aditi Sharma

C#

using System;
 
class GFG {
 
     // A dynamic programming based
     // function to find nth
     // Catalan number
     static uint catalanDP( uint n)
     {
         // Table to store results of subproblems
         uint [] catalan = new uint [n + 2];
 
         // Initialize first two values in table
         catalan[0] = catalan[1] = 1;
 
         // Fill entries in catalan[]
         // using recursive formula
         for ( uint i = 2; i <= n; i++) {
             catalan[i] = 0;
             for ( uint j = 0; j < i; j++)
                 catalan[i]
                     += catalan[j] * catalan[i - j - 1];
         }
 
         // Return last entry
         return catalan[n];
     }
 
     // Driver code
     static void Main()
     {
         for ( uint i = 0; i < 10; i++)
             Console.Write(catalanDP(i) + " " );
     }
}
 
// This code is contributed by Chandan_jnu

的PHP

<?php
// PHP program for nth Catalan Number
 
// A dynamic programming based function
// to find nth Catalan number
function catalanDP( $n )
{
     
     // Table to store results
     // of subproblems
     $catalan = array ();
 
     // Initialize first two
     // values in table
     $catalan [0] = $catalan [1] = 1;
 
     // Fill entries in catalan[]
     // using recursive formula
     for ( $i = 2; $i <= $n ; $i ++)
     {
         $catalan [ $i ] = 0;
         for ( $j = 0; $j < $i ; $j ++)
             $catalan [ $i ] += $catalan [ $j ] *
                    $catalan [ $i - $j - 1];
     }
 
     // Return last entry
     return $catalan [ $n ];
}
 
     // Driver Code
     for ( $i = 0; $i < 10; $i ++)
         echo catalanDP( $i ) , " " ;
 
// This code is contributed anuj_67.
?>

输出如下

1 1 2 5 14 42 132 429 1430 4862

时间复杂度：上述实现的时间复杂度为O(n^2)

使用二项式系数

我们还可以使用以下公式在O(n)时间中找到第n个卡塔兰数字。

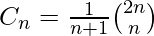
C_n = \ frac {1} {n + 1} \ binom {2n} {n}

我们已经讨论了O(n)方法求二项式系数nCr.

C ++

// C++ program for nth Catalan Number
#include <iostream>
using namespace std;
 
// Returns value of Binomial Coefficient C(n, k)
unsigned long int binomialCoeff(unsigned int n, unsigned int k)
{
     unsigned long int res = 1;
 
     // Since C(n, k) = C(n, n-k)
     if (k > n - k)
         k = n - k;
 
     // Calculate value of [n*(n-1)*---*(n-k+1)] /
     // [k*(k-1)*---*1]
     for ( int i = 0; i < k; ++i) {
         res *= (n - i);
         res /= (i + 1);
     }
 
     return res;
}
 
// A Binomial coefficient based function to find nth catalan
// number in O(n) time
unsigned long int catalan(unsigned int n)
{
     // Calculate value of 2nCn
     unsigned long int c = binomialCoeff(2 * n, n);
 
     // return 2nCn/(n+1)
     return c / (n + 1);
}
 
// Driver code
int main()
{
     for ( int i = 0; i < 10; i++)
         cout << catalan(i) << " " ;
     return 0;
}

Java

// Java program for nth Catalan Number
 
class GFG {
 
     // Returns value of Binomial Coefficient C(n, k)
     static long binomialCoeff( int n, int k)
     {
         long res = 1 ;
 
         // Since C(n, k) = C(n, n-k)
         if (k > n - k) {
             k = n - k;
         }
 
         // Calculate value of [n*(n-1)*---*(n-k+1)] /
         // [k*(k-1)*---*1]
         for ( int i = 0 ; i < k; ++i) {
             res *= (n - i);
             res /= (i + 1 );
         }
 
         return res;
     }
 
     // A Binomial coefficient based function
     //  to find nth catalan number in O(n) time
     static long catalan( int n)
     {
         // Calculate value of 2nCn
         long c = binomialCoeff( 2 * n, n);
 
         // return 2nCn/(n+1)
         return c / (n + 1 );
     }
 
     // Driver code
     public static void main(String[] args)
     {
         for ( int i = 0 ; i < 10 ; i++) {
             System.out.print(catalan(i) + " " );
         }
     }
}

Python3

# Python program for nth Catalan Number
# Returns value of Binomial Coefficient C(n, k)
 
 
def binomialCoefficient(n, k):
 
     # since C(n, k) = C(n, n - k)
     if (k > n - k):
         k = n - k
 
     # initialize result
     res = 1
 
     # Calculate value of [n * (n-1) *---* (n-k + 1)]
     # / [k * (k-1) *----* 1]
     for i in range (k):
         res = res * (n - i)
         res = res / (i + 1 )
     return res
 
# A Binomial coefficient based function to
# find nth catalan number in O(n) time
 
 
def catalan(n):
     c = binomialCoefficient( 2 * n, n)
     return c / (n + 1 )
 
# Driver Code
for i in range ( 10 ):
     print (catalan(i), end = " " )
 
# This code is contributed by Aditi Sharma

C#

// C# program for nth Catalan Number
using System;
class GFG {
 
     // Returns value of Binomial Coefficient C(n, k)
     static long binomialCoeff( int n, int k)
     {
         long res = 1;
 
         // Since C(n, k) = C(n, n-k)
         if (k > n - k) {
             k = n - k;
         }
 
         // Calculate value of [n*(n-1)*---*(n-k+1)] /
         // [k*(k-1)*---*1]
         for ( int i = 0; i < k; ++i) {
             res *= (n - i);
             res /= (i + 1);
         }
 
         return res;
     }
 
     // A Binomial coefficient based function to find nth
     // catalan number in O(n) time
     static long catalan( int n)
     {
         // Calculate value of 2nCn
         long c = binomialCoeff(2 * n, n);
 
         // return 2nCn/(n+1)
         return c / (n + 1);
     }
 
     // Driver code
     public static void Main()
     {
         for ( int i = 0; i < 10; i++) {
             Console.Write(catalan(i) + " " );
         }
     }
}
 
// This code is contributed
// by Akanksha Rai

的PHP

<?php
// PHP program for nth Catalan Number
 
// Returns value of Binomial
// Coefficient C(n, k)
function binomialCoeff( $n , $k )
{
     $res = 1;
 
     // Since C(n, k) = C(n, n-k)
     if ( $k > $n - $k )
         $k = $n - $k ;
 
     // Calculate value of [n*(n-1)*---*(n-k+1)] /
     //                    [k*(k-1)*---*1]
     for ( $i = 0; $i < $k ; ++ $i )
     {
         $res *= ( $n - $i );
         $res = floor ( $res / ( $i + 1));
     }
 
     return $res ;
}
 
// A Binomial coefficient based function
// to find nth catalan number in O(n) time
function catalan( $n )
{
     // Calculate value of 2nCn
     $c = binomialCoeff(2 * ( $n ), $n );
 
     // return 2nCn/(n+1)
     return floor ( $c / ( $n + 1));
}
 
// Driver code
for ( $i = 0; $i < 10; $i ++)
echo catalan( $i ), " " ;
 
// This code is contributed by Ryuga
?>

输出如下

1 1 2 5 14 42 132 429 1430 4862

时间复杂度：

上述实现的时间复杂度为O(n)。

我们还可以使用以下公式在O(n)时间中找到第n个卡塔兰数。

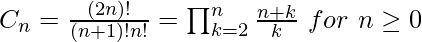
C_n = \ frac {（2n）！} {（n + 1）！n！} = \ prod_ {k = 2} ^ {n} \ frac {n + k} {k} \表示\ n \ geq 0

使用多精度库：在这种方法中, 我们使用了boost多精度库, 其使用的动机只是在找到大型CATALAN数的同时, 还具有精确性, 并且使用了for循环的通用技术来计算卡塔兰数。

例如：N = 5最初设置cat_ = 1然后打印cat_, 然后对于i = 1从i = 1迭代到i <5； cat_ = cat_ *(4 * 1-2)= 1 * 2 = 2 cat_ = cat_ /(i + 1)= 2/2 = 1对于i = 2; cat_ = cat_ *(4 * 2-2)= 1 * 6 = 6 cat_ = cat_ /(i + 1)= 6/3 = 2对于i = 3：-cat_ = cat_ *(4 * 3-2)= 2 * 10 = 20 cat_ = cat_ /(i + 1)= 20/4 = 5对于i = 4：-cat_ = cat_ *(4 * 4-2)= 5 * 14 = 70 cat_ = cat_ /(i + 1)= 70/5 = 14

伪代码：

a) initially set cat_=1 and print it
b) run a for loop i=1 to i<=n
            cat_ *= (4*i-2)
            cat_ /= (i+1)
            print cat_
c) end loop and exit

C ++

#include <bits/stdc++.h>
#include <boost/multiprecision/cpp_int.hpp>
using boost::multiprecision::cpp_int;
using namespace std;
 
// Function to print the number
void catalan( int n)
{
     cpp_int cat_ = 1;
 
     // For the first number
     cout << cat_ << " " ; // C(0)
 
     // Iterate till N
     for (cpp_int i = 1; i < n; i++)
     {
         // Calculate the number
         // and print it
         cat_ *= (4 * i - 2);
         cat_ /= (i + 1);
         cout << cat_ << " " ;
     }
}
 
// Driver code
int main()
{
     int n = 5;
 
     // Function call
     catalan(n);
     return 0;
}

输出如下

1 1 2 5 14

时间复杂度：O(n)

辅助空间：O(1)

在Java中使用BigInteger的另一种解决方案：

  • 即使在Java中使用long也不可能找到N> 80的卡塔兰数字值, 因此我们使用BigInteger
  • 在这里, 我们找到了使用上述二项式系数法的解决方案

Java

import java.io.*;
import java.util.*;
import java.math.*;
 
class GFG
{
     public static BigInteger findCatalan( int n)
     {
         // using BigInteger to calculate large factorials
         BigInteger b = new BigInteger( "1" );
 
         // calculating n!
         for ( int i = 1 ; i <= n; i++) {
             b = b.multiply(BigInteger.valueOf(i));
         }
 
         // calculating n! * n!
         b = b.multiply(b);
 
         BigInteger d = new BigInteger( "1" );
 
         // calculating (2n)!
         for ( int i = 1 ; i <= 2 * n; i++) {
             d = d.multiply(BigInteger.valueOf(i));
         }
 
         // calculating (2n)! / (n! * n!)
         BigInteger ans = d.divide(b);
 
         // calculating (2n)! / ((n! * n!) * (n+1))
         ans = ans.divide(BigInteger.valueOf(n + 1 ));
         return ans;
     }
   
     // Driver Code
     public static void main(String[] args)
     {
         int n = 5 ;
         System.out.println(findCatalan(n));
     }
}
// Contributed by Rohit Oberoi

输出如下

42

参考文献：

http://en.wikipedia.org/wiki/Catalan_number

如果发现任何不正确的地方, 或者想分享有关上述主题的更多信息, 请发表评论。

木子山

发表评论

:?: :razz: :sad: :evil: :!: :smile: :oops: :grin: :eek: :shock: :???: :cool: :lol: :mad: :twisted: :roll: :wink: :idea: :arrow: :neutral: :cry: :mrgreen: