算法设计：计算无向图的欧拉路径和回路？

本文概述

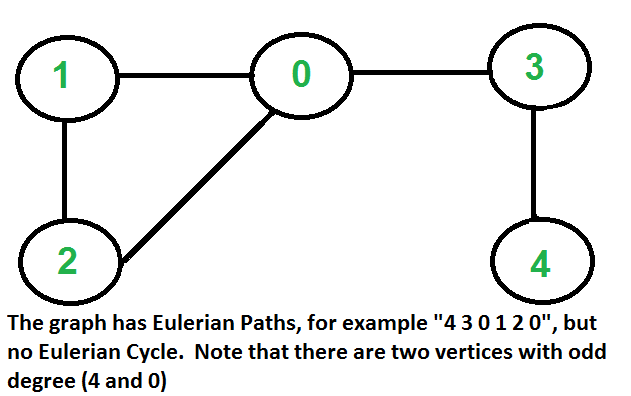
欧拉路径是图形中的一条路径, 该路径恰好一次访问每个边。欧拉回路是一条始于和终止于同一顶点的欧拉路径。

如何查找给定图是否为欧拉图？

问题与以下问题相同。 "有可能画出给定的图形而无需从纸上抬起铅笔, 也不必多次描画任何边缘。"

如果图形具有欧拉循环, 则称为欧拉曲线；如果图形具有欧拉路径, 则称为半欧拉曲线。问题似乎类似于哈密​​顿路径这是一般图的NP完全问题。幸运的是, 我们可以发现给定图在多项式时间内是否具有欧拉路径。实际上, 我们可以在O(V + E)时间找到它。

以下是具有欧拉路径和循环的无向图的一些有趣特性。我们可以使用这些属性来查找图是否为欧拉图。

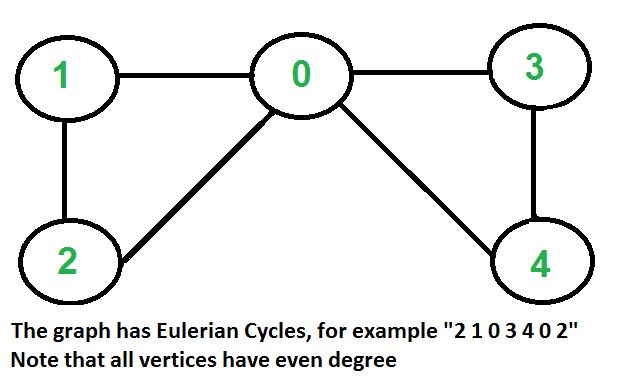
欧拉循环

如果满足以下两个条件, 则无向图具有欧拉循环。

….a)所有非零度的顶点都已连接。我们不在乎零度的顶点, 因为它们不属于欧拉循环或路径(我们仅考虑所有边)。

….b)所有顶点都具有偶数度。

欧拉路径

如果满足以下两个条件, 则无向图具有欧拉路径。

….a)与欧拉循环的条件(a)相同

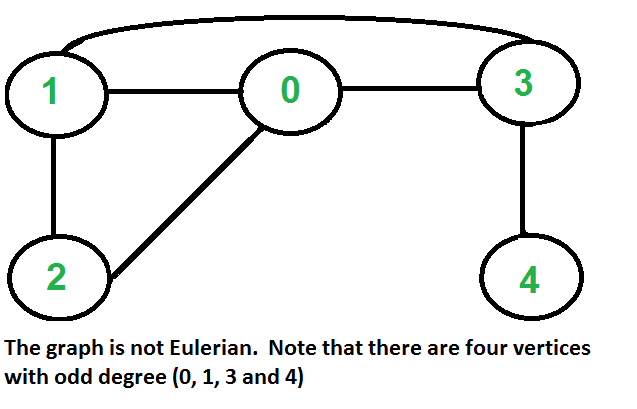
….b)如果零个或两个顶点具有奇数度, 而所有其他顶点具有偶数度。请注意, 在无向图中, 只有一个具有奇数度的顶点是不可能的(在无向图中, 所有度的总和始终是偶数)

请注意, 没有边的图被视为欧拉图, 因为没有要遍历的边。

这是如何运作的？

在欧拉路径中, 每次访问顶点v时, 我们都会走过两个未访问的边缘, 且端点的端点为v。因此, 欧拉路径中的所有中间顶点都必须具有均匀度。对于欧拉循环, 任何顶点都可以是中间顶点, 因此所有顶点都必须具有偶数度。

C ++

// A C++ program to check if a given graph is Eulerian or not
#include<iostream>
#include <list>
using namespace std;
  
// A class that represents an undirected graph
class Graph
{
     int V;    // No. of vertices
     list< int > *adj;    // A dynamic array of adjacency lists
public :
     // Constructor and destructor
     Graph( int V)   { this ->V = V; adj = new list< int >[V]; }
     ~Graph() { delete [] adj; } // To avoid memory leak
  
      // function to add an edge to graph
     void addEdge( int v, int w);
  
     // Method to check if this graph is Eulerian or not
     int isEulerian();
  
     // Method to check if all non-zero degree vertices are connected
     bool isConnected();
  
     // Function to do DFS starting from v. Used in isConnected();
     void DFSUtil( int v, bool visited[]);
};
  
void Graph::addEdge( int v, int w)
{
     adj[v].push_back(w);
     adj[w].push_back(v);  // Note: the graph is undirected
}
  
void Graph::DFSUtil( int v, bool visited[])
{
     // Mark the current node as visited and print it
     visited[v] = true ;
  
     // Recur for all the vertices adjacent to this vertex
     list< int >::iterator i;
     for (i = adj[v].begin(); i != adj[v].end(); ++i)
         if (!visited[*i])
             DFSUtil(*i, visited);
}
  
// Method to check if all non-zero degree vertices are connected.
// It mainly does DFS traversal starting from
bool Graph::isConnected()
{
     // Mark all the vertices as not visited
     bool visited[V];
     int i;
     for (i = 0; i < V; i++)
         visited[i] = false ;
  
     // Find a vertex with non-zero degree
     for (i = 0; i < V; i++)
         if (adj[i].size() != 0)
             break ;
  
     // If there are no edges in the graph, return true
     if (i == V)
         return true ;
  
     // Start DFS traversal from a vertex with non-zero degree
     DFSUtil(i, visited);
  
     // Check if all non-zero degree vertices are visited
     for (i = 0; i < V; i++)
        if (visited[i] == false && adj[i].size() > 0)
             return false ;
  
     return true ;
}
  
/* The function returns one of the following values
    0 --> If grpah is not Eulerian
    1 --> If graph has an Euler path (Semi-Eulerian)
    2 --> If graph has an Euler Circuit (Eulerian)  */
int Graph::isEulerian()
{
     // Check if all non-zero degree vertices are connected
     if (isConnected() == false )
         return 0;
  
     // Count vertices with odd degree
     int odd = 0;
     for ( int i = 0; i < V; i++)
         if (adj[i].size() & 1)
             odd++;
  
     // If count is more than 2, then graph is not Eulerian
     if (odd > 2)
         return 0;
  
     // If odd count is 2, then semi-eulerian.
     // If odd count is 0, then eulerian
     // Note that odd count can never be 1 for undirected graph
     return (odd)? 1 : 2;
}
  
// Function to run test cases
void test(Graph &g)
{
     int res = g.isEulerian();
     if (res == 0)
         cout << "graph is not Eulerian\n" ;
     else if (res == 1)
         cout << "graph has a Euler path\n" ;
     else
         cout << "graph has a Euler cycle\n" ;
}
  
// Driver program to test above function
int main()
{
     // Let us create and test graphs shown in above figures
     Graph g1(5);
     g1.addEdge(1, 0);
     g1.addEdge(0, 2);
     g1.addEdge(2, 1);
     g1.addEdge(0, 3);
     g1.addEdge(3, 4);
     test(g1);
  
     Graph g2(5);
     g2.addEdge(1, 0);
     g2.addEdge(0, 2);
     g2.addEdge(2, 1);
     g2.addEdge(0, 3);
     g2.addEdge(3, 4);
     g2.addEdge(4, 0);
     test(g2);
  
     Graph g3(5);
     g3.addEdge(1, 0);
     g3.addEdge(0, 2);
     g3.addEdge(2, 1);
     g3.addEdge(0, 3);
     g3.addEdge(3, 4);
     g3.addEdge(1, 3);
     test(g3);
  
     // Let us create a graph with 3 vertices
     // connected in the form of cycle
     Graph g4(3);
     g4.addEdge(0, 1);
     g4.addEdge(1, 2);
     g4.addEdge(2, 0);
     test(g4);
  
     // Let us create a graph with all veritces
     // with zero degree
     Graph g5(3);
     test(g5);
  
     return 0;
}

Java

// A Java program to check if a given graph is Eulerian or not
import java.io.*;
import java.util.*;
import java.util.LinkedList;
  
// This class represents an undirected graph using adjacency list
// representation
class Graph
{
     private int V;   // No. of vertices
  
     // Array  of lists for Adjacency List Representation
     private LinkedList<Integer> adj[];
  
     // Constructor
     Graph( int v)
     {
         V = v;
         adj = new LinkedList[v];
         for ( int i= 0 ; i<v; ++i)
             adj[i] = new LinkedList();
     }
  
     //Function to add an edge into the graph
     void addEdge( int v, int w)
     {
         adj[v].add(w); // Add w to v's list.
         adj[w].add(v); //The graph is undirected
     }
  
     // A function used by DFS
     void DFSUtil( int v, boolean visited[])
     {
         // Mark the current node as visited
         visited[v] = true ;
  
         // Recur for all the vertices adjacent to this vertex
         Iterator<Integer> i = adj[v].listIterator();
         while (i.hasNext())
         {
             int n = i.next();
             if (!visited[n])
                 DFSUtil(n, visited);
         }
     }
  
     // Method to check if all non-zero degree vertices are
     // connected. It mainly does DFS traversal starting from
     boolean isConnected()
     {
         // Mark all the vertices as not visited
         boolean visited[] = new boolean [V];
         int i;
         for (i = 0 ; i < V; i++)
             visited[i] = false ;
  
         // Find a vertex with non-zero degree
         for (i = 0 ; i < V; i++)
             if (adj[i].size() != 0 )
                 break ;
  
         // If there are no edges in the graph, return true
         if (i == V)
             return true ;
  
         // Start DFS traversal from a vertex with non-zero degree
         DFSUtil(i, visited);
  
         // Check if all non-zero degree vertices are visited
         for (i = 0 ; i < V; i++)
            if (visited[i] == false && adj[i].size() > 0 )
                 return false ;
  
         return true ;
     }
  
     /* The function returns one of the following values
        0 --> If grpah is not Eulerian
        1 --> If graph has an Euler path (Semi-Eulerian)
        2 --> If graph has an Euler Circuit (Eulerian)  */
     int isEulerian()
     {
         // Check if all non-zero degree vertices are connected
         if (isConnected() == false )
             return 0 ;
  
         // Count vertices with odd degree
         int odd = 0 ;
         for ( int i = 0 ; i < V; i++)
             if (adj[i].size()% 2 != 0 )
                 odd++;
  
         // If count is more than 2, then graph is not Eulerian
         if (odd > 2 )
             return 0 ;
  
         // If odd count is 2, then semi-eulerian.
         // If odd count is 0, then eulerian
         // Note that odd count can never be 1 for undirected graph
         return (odd== 2 )? 1 : 2 ;
     }
  
     // Function to run test cases
     void test()
     {
         int res = isEulerian();
         if (res == 0 )
             System.out.println( "graph is not Eulerian" );
         else if (res == 1 )
             System.out.println( "graph has a Euler path" );
         else
            System.out.println( "graph has a Euler cycle" );
     }
  
     // Driver method
     public static void main(String args[])
     {
         // Let us create and test graphs shown in above figures
         Graph g1 = new Graph( 5 );
         g1.addEdge( 1 , 0 );
         g1.addEdge( 0 , 2 );
         g1.addEdge( 2 , 1 );
         g1.addEdge( 0 , 3 );
         g1.addEdge( 3 , 4 );
         g1.test();
  
         Graph g2 = new Graph( 5 );
         g2.addEdge( 1 , 0 );
         g2.addEdge( 0 , 2 );
         g2.addEdge( 2 , 1 );
         g2.addEdge( 0 , 3 );
         g2.addEdge( 3 , 4 );
         g2.addEdge( 4 , 0 );
         g2.test();
  
         Graph g3 = new Graph( 5 );
         g3.addEdge( 1 , 0 );
         g3.addEdge( 0 , 2 );
         g3.addEdge( 2 , 1 );
         g3.addEdge( 0 , 3 );
         g3.addEdge( 3 , 4 );
         g3.addEdge( 1 , 3 );
         g3.test();
  
         // Let us create a graph with 3 vertices
         // connected in the form of cycle
         Graph g4 = new Graph( 3 );
         g4.addEdge( 0 , 1 );
         g4.addEdge( 1 , 2 );
         g4.addEdge( 2 , 0 );
         g4.test();
  
         // Let us create a graph with all veritces
         // with zero degree
         Graph g5 = new Graph( 3 );
         g5.test();
     }
}
// This code is contributed by Aakash Hasija

python

# Python program to check if a given graph is Eulerian or not
#Complexity : O(V+E)
   
from collections import defaultdict
   
#This class represents a undirected graph using adjacency list representation
class Graph:
   
     def __init__( self , vertices):
         self .V = vertices #No. of vertices
         self .graph = defaultdict( list ) # default dictionary to store graph
   
     # function to add an edge to graph
     def addEdge( self , u, v):
         self .graph[u].append(v)
         self .graph[v].append(u)
   
     #A function used by isConnected
     def DFSUtil( self , v, visited):
         # Mark the current node as visited 
         visited[v] = True
  
         #Recur for all the vertices adjacent to this vertex
         for i in self .graph[v]:
             if visited[i] = = False :
                 self .DFSUtil(i, visited)
   
   
     '''Method to check if all non-zero degree vertices are
     connected. It mainly does DFS traversal starting from 
     node with non-zero degree'''
     def isConnected( self ):
   
         # Mark all the vertices as not visited
         visited = [ False ] * ( self .V)
  
         #  Find a vertex with non-zero degree
         for i in range ( self .V):
             if len ( self .graph[i]) > 1 :
                 break
  
         # If there are no edges in the graph, return true
         if i = = self .V - 1 :
             return True
  
         # Start DFS traversal from a vertex with non-zero degree
         self .DFSUtil(i, visited)
  
         # Check if all non-zero degree vertices are visited
         for i in range ( self .V):
             if visited[i] = = False and len ( self .graph[i]) > 0 :
                 return False
          
         return True
  
  
     '''The function returns one of the following values
        0 --> If grpah is not Eulerian
        1 --> If graph has an Euler path (Semi-Eulerian)
        2 --> If graph has an Euler Circuit (Eulerian)  '''
     def isEulerian( self ):
         # Check if all non-zero degree vertices are connected
         if self .isConnected() = = False :
             return 0
         else :
             #Count vertices with odd degree
             odd = 0
             for i in range ( self .V):
                 if len ( self .graph[i]) % 2 ! = 0 :
                     odd + = 1
  
             '''If odd count is 2, then semi-eulerian.
             If odd count is 0, then eulerian
             If count is more than 2, then graph is not Eulerian
             Note that odd count can never be 1 for undirected graph'''
             if odd = = 0 :
                 return 2
             elif odd = = 2 :
                 return 1
             elif odd > 2 :
                 return 0
  
  
      # Function to run test cases
      def test( self ):
          res = self .isEulerian()
          if res = = 0 :
              print "graph is not Eulerian"
          elif res = = 1 :
              print "graph has a Euler path"
          else :
              print "graph has a Euler cycle"
   
   
  
#Let us create and test graphs shown in above figures
g1 = Graph( 5 );
g1.addEdge( 1 , 0 )
g1.addEdge( 0 , 2 )
g1.addEdge( 2 , 1 )
g1.addEdge( 0 , 3 )
g1.addEdge( 3 , 4 )
g1.test()
  
g2 = Graph( 5 )
g2.addEdge( 1 , 0 )
g2.addEdge( 0 , 2 )
g2.addEdge( 2 , 1 )
g2.addEdge( 0 , 3 )
g2.addEdge( 3 , 4 )
g2.addEdge( 4 , 0 )
g2.test();
  
g3 = Graph( 5 )
g3.addEdge( 1 , 0 )
g3.addEdge( 0 , 2 )
g3.addEdge( 2 , 1 )
g3.addEdge( 0 , 3 )
g3.addEdge( 3 , 4 )
g3.addEdge( 1 , 3 )
g3.test()
  
#Let us create a graph with 3 vertices
# connected in the form of cycle
g4 = Graph( 3 )
g4.addEdge( 0 , 1 )
g4.addEdge( 1 , 2 )
g4.addEdge( 2 , 0 )
g4.test()
  
# Let us create a graph with all veritces
# with zero degree
g5 = Graph( 3 )
g5.test()
  
#This code is contributed by Neelam Yadav

C#

// A C# program to check if a given graph is Eulerian or not
using System;
using System.Collections.Generic;
  
   
// This class represents an undirected graph using adjacency list
// representation
public class Graph
{
     private int V;   // No. of vertices
   
     // Array  of lists for Adjacency List Representation
     private List< int > []adj;
   
     // Constructor
     Graph( int v)
     {
         V = v;
         adj = new List< int >[v];
         for ( int i=0; i<v; ++i)
             adj[i] = new List< int >();
     }
   
     //Function to add an edge into the graph
     void addEdge( int v, int w)
     {
         adj[v].Add(w); // Add w to v's list.
         adj[w].Add(v); //The graph is undirected
     }
   
     // A function used by DFS
     void DFSUtil( int v, bool []visited)
     {
         // Mark the current node as visited
         visited[v] = true ;
   
         // Recur for all the vertices adjacent to this vertex
         foreach ( int i in adj[v]){
             int n = i;
             if (!visited[n])
                 DFSUtil(n, visited);
         }
     }
   
     // Method to check if all non-zero degree vertices are
     // connected. It mainly does DFS traversal starting from
     bool isConnected()
     {
         // Mark all the vertices as not visited
         bool []visited = new bool [V];
         int i;
         for (i = 0; i < V; i++)
             visited[i] = false ;
   
         // Find a vertex with non-zero degree
         for (i = 0; i < V; i++)
             if (adj[i].Count != 0)
                 break ;
   
         // If there are no edges in the graph, return true
         if (i == V)
             return true ;
   
         // Start DFS traversal from a vertex with non-zero degree
         DFSUtil(i, visited);
   
         // Check if all non-zero degree vertices are visited
         for (i = 0; i < V; i++)
            if (visited[i] == false && adj[i].Count > 0)
                 return false ;
   
         return true ;
     }
   
     /* The function returns one of the following values
        0 --> If grpah is not Eulerian
        1 --> If graph has an Euler path (Semi-Eulerian)
        2 --> If graph has an Euler Circuit (Eulerian)  */
     int isEulerian()
     {
         // Check if all non-zero degree vertices are connected
         if (isConnected() == false )
             return 0;
   
         // Count vertices with odd degree
         int odd = 0;
         for ( int i = 0; i < V; i++)
             if (adj[i].Count%2!=0)
                 odd++;
   
         // If count is more than 2, then graph is not Eulerian
         if (odd > 2)
             return 0;
   
         // If odd count is 2, then semi-eulerian.
         // If odd count is 0, then eulerian
         // Note that odd count can never be 1 for undirected graph
         return (odd==2)? 1 : 2;
     }
   
     // Function to run test cases
     void test()
     {
         int res = isEulerian();
         if (res == 0)
             Console.WriteLine( "graph is not Eulerian" );
         else if (res == 1)
             Console.WriteLine( "graph has a Euler path" );
         else
            Console.WriteLine( "graph has a Euler cycle" );
     }
   
     // Driver method
     public static void Main(String []args)
     {
         // Let us create and test graphs shown in above figures
         Graph g1 = new Graph(5);
         g1.addEdge(1, 0);
         g1.addEdge(0, 2);
         g1.addEdge(2, 1);
         g1.addEdge(0, 3);
         g1.addEdge(3, 4);
         g1.test();
   
         Graph g2 = new Graph(5);
         g2.addEdge(1, 0);
         g2.addEdge(0, 2);
         g2.addEdge(2, 1);
         g2.addEdge(0, 3);
         g2.addEdge(3, 4);
         g2.addEdge(4, 0);
         g2.test();
   
         Graph g3 = new Graph(5);
         g3.addEdge(1, 0);
         g3.addEdge(0, 2);
         g3.addEdge(2, 1);
         g3.addEdge(0, 3);
         g3.addEdge(3, 4);
         g3.addEdge(1, 3);
         g3.test();
   
         // Let us create a graph with 3 vertices
         // connected in the form of cycle
         Graph g4 = new Graph(3);
         g4.addEdge(0, 1);
         g4.addEdge(1, 2);
         g4.addEdge(2, 0);
         g4.test();
   
         // Let us create a graph with all veritces
         // with zero degree
         Graph g5 = new Graph(3);
         g5.test();
     }
}
  
// This code contributed by PrinciRaj1992

输出如下：

graph has a Euler path
graph has a Euler cycle
graph is not Eulerian
graph has a Euler cycle
graph has a Euler cycle

时间复杂度：O(V + E)

下一篇文章：

有向图的欧拉路径和电路。

Fleury的算法可以打印欧拉路径或电路？

参考文献：

http://en.wikipedia.org/wiki/Eulerian_path

如果发现任何不正确的地方, 或者你想分享有关上述主题的更多信息, 请发表评论