使用30分钟快速入门机器学习时间

1.下载, 安装和启动Python SciPy

如果尚未安装Python和SciPy平台, 请在你的系统上安装它。可以轻松地遵循它的安装指南。

1.1安装SciPy库

使用Python 2.7或3.5以上版本。

你将需要安装5个密钥库。以下是本教程所需的Python SciPy库的列表：

• 科学的
• Numpy
• matplotlib
• 大熊猫
• 斯克莱恩

1.2启动Python并检查版本

确保你的Python环境已成功安装并且可以正常工作是一个好主意。

下面的脚本将有助于测试环境。它将导入本教程所需的每个库并打印版本。

输入或复制并粘贴以下脚本：

# Check the versions of libraries
  
# Python version
import sys
print ( 'Python: {}' . format (sys.version))
# scipy
import scipy
print ( 'scipy: {}' . format (scipy.__version__))
# numpy
import numpy
print ( 'numpy: {}' . format (numpy.__version__))
# matplotlib
import matplotlib
print ( 'matplotlib: {}' . format (matplotlib.__version__))
# pandas
import pandas
print ( 'pandas: {}' . format (pandas.__version__))
# scikit-learn
import sklearn
print ( 'sklearn: {}' . format (sklearn.__version__))

如果出现错误, 请停止。现在该修复它了。

2.加载数据。

数据集–

虹膜数据

它是著名的数据, 几乎被每个人用作机器学习和统计中的" hello world"数据集。

数据集包含150个鸢尾花的观测值。花的测量单位有四列, 以厘米为单位。第五列是观察到的花的种类。所有观察到的花均属于三种。

2.1导入库

首先, 让我们导入要使用的所有模块, 功能和对象。

# Load libraries
  
import pandas
from pandas.plotting import scatter_matrix
import matplotlib.pyplot as plt
from sklearn import model_selection
from sklearn.metrics import classification_report
from sklearn.metrics import confusion_matrix
from sklearn.metrics import accuracy_score
from sklearn.linear_model import LogisticRegression
from sklearn.tree import DecisionTreeClassifier
from sklearn.neighbors import KNeighborsClassifier
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis
from sklearn.naive_bayes import GaussianNB
from sklearn.svm import SVC

在继续操作之前, 需要一个工作的SciPy环境。

2.2加载数据集

数据可以直接加载到UCI机器学习存储库中。

使用熊猫加载数据并探索描述性统计数据和数据可视化。

注–加载数据时指定每列的名称。这将在以后探索数据时提供帮助。

url = 
"https://raw.githubusercontent.com / jbrownlee / Datasets / master / iris.csv"
names = [ 'sepal-length' , 'sepal-width' , 'petal-length' , 'petal-width' , 'class' ]
dataset = pandas.read_csv(url, names = names)

如果确实存在网络问题, 则可以将iris.csv文件下载到工作目录中, 并使用相同的方法将URL更改为本地文件名来加载它。

3.汇总数据集

现在该看一下数据了。

以几种不同方式查看数据的步骤：

• 数据集的尺寸。
• 窥视数据本身。
• 所有属性的统计摘要。
• 通过类变量对数据进行分类。

3.1数据集维度

# shape
print (dataset.shape)

(150, 5)

3.2查看数据

# head
print (dataset.head( 20 ))

sepal-length  sepal-width  petal-length  petal-width        class
0            5.1          3.5           1.4          0.2  Iris-setosa
1            4.9          3.0           1.4          0.2  Iris-setosa
2            4.7          3.2           1.3          0.2  Iris-setosa
3            4.6          3.1           1.5          0.2  Iris-setosa
4            5.0          3.6           1.4          0.2  Iris-setosa
5            5.4          3.9           1.7          0.4  Iris-setosa
6            4.6          3.4           1.4          0.3  Iris-setosa
7            5.0          3.4           1.5          0.2  Iris-setosa
8            4.4          2.9           1.4          0.2  Iris-setosa
9            4.9          3.1           1.5          0.1  Iris-setosa
10           5.4          3.7           1.5          0.2  Iris-setosa
11           4.8          3.4           1.6          0.2  Iris-setosa
12           4.8          3.0           1.4          0.1  Iris-setosa
13           4.3          3.0           1.1          0.1  Iris-setosa
14           5.8          4.0           1.2          0.2  Iris-setosa
15           5.7          4.4           1.5          0.4  Iris-setosa
16           5.4          3.9           1.3          0.4  Iris-setosa
17           5.1          3.5           1.4          0.3  Iris-setosa
18           5.7          3.8           1.7          0.3  Iris-setosa
19           5.1          3.8           1.5          0.3  Iris-setosa

3.3统计摘要

这包括计数, 平均值, 最小值和最大值以及一些百分位数。

# descriptions
print (dataset.describe())

清楚可见, 所有数值都具有相同的标度(厘米)和相似的范围(介于0到8厘米之间)。

sepal-length  sepal-width  petal-length  petal-width
count    150.000000   150.000000    150.000000   150.000000
mean       5.843333     3.054000      3.758667     1.198667
std        0.828066     0.433594      1.764420     0.763161
min        4.300000     2.000000      1.000000     0.100000
25%        5.100000     2.800000      1.600000     0.300000
50%        5.800000     3.000000      4.350000     1.300000
75%        6.400000     3.300000      5.100000     1.800000
max        7.900000     4.400000      6.900000     2.500000

3.4班级分布

# class distribution
print (dataset.groupby( 'class' ).size())

class
Iris-setosa        50
Iris-versicolor    50
Iris-virginica     50

4.数据可视化

使用两种类型的图：

1. 单变量图可以更好地理解每个属性。
2. 多变量图可更好地了解属性之间的关系。

4.1单变量图

单变量图–每个单独变量的图。

假设输入变量是数字变量, 我们可以为每个变量创建箱形图和晶须图。

# box and whisker plots
dataset.plot(kind = 'box' , subplots = True , layout = ( 2 , 2 ), sharex = False , sharey = False )
plt.show()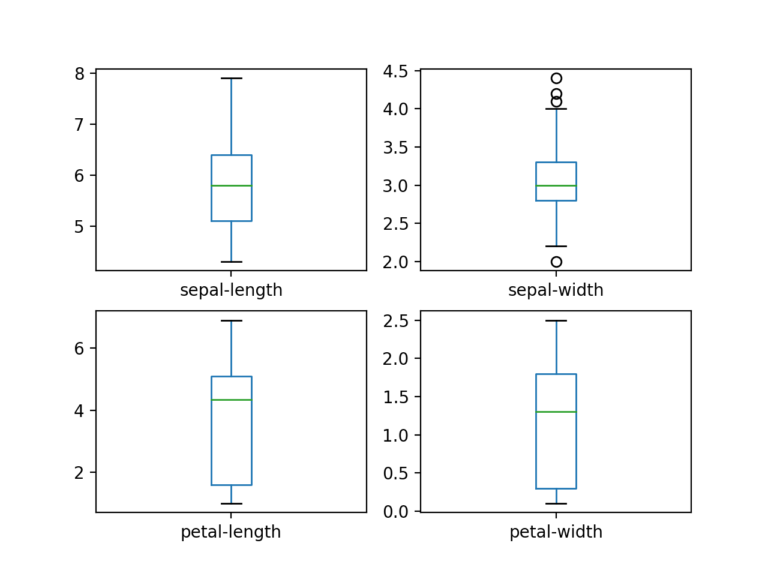

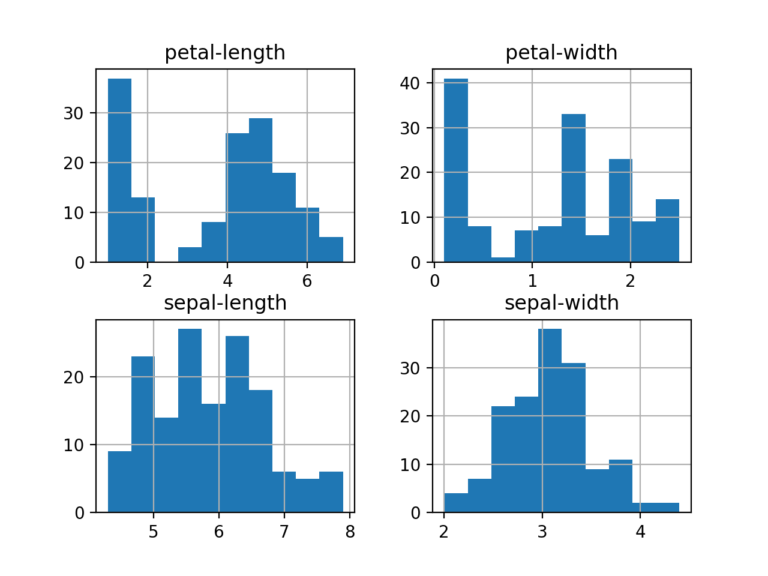
为每个输入变量创建直方图, 以了解分布情况。

# histograms
dataset.hist()
plt.show()

看起来其中两个输入变量具有高斯分布。注意这一点很有用, 因为我们可以使用可以利用此假设的算法。

4.2多元图

变量之间的相互作用。

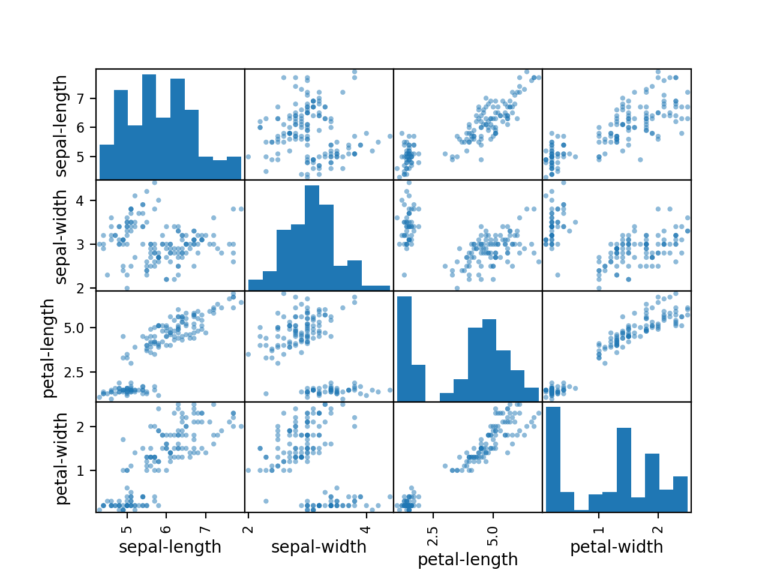
首先, 让我们看看所有属性对的散点图。这有助于发现输入变量之间的结构化关系。

# scatter plot matrix
scatter_matrix(dataset)
plt.show()

注意一些属性对的对角线分组。这表明高度相关性和可预测的关系。

5.评估一些算法

创建一些数据模型并估计它们在看不见的数据上的准确性。

1. 分离出验证数据集。
2. 设置测试工具以使用10倍交叉验证。
3. 建立5种不同的模型以根据花的测量预测物种
4. 选择最佳型号。

5.1创建验证数据集

使用统计方法来估计我们在看不见的数据上创建的模型的准确性。通过对实际看不见的数据进行评估, 可以得出最佳模型对看不见数据的准确性的具体估计。

一些数据被用作算法不会看到的测试数据, 并且这些数据被用来获得第二个独立的想法, 即最佳模型实际上可能有多精确。

测试数据分为两部分, 其中80％将用于训练模型, 而20％将作为验证数据集。

# Split-out validation dataset
array = dataset.values
X = array[:, 0 : 4 ]
Y = array[:, 4 ]
validation_size = 0.20
seed = 7
X_train, X_validation, Y_train, Y_validation = model_selection.train_test_split(
         X, Y, test_size = validation_size, random_state = seed)

X_train和Y_train是用于准备模型的训练数据, 以后可以使用X_validation和Y_validation集。

5.2测试线束

使用10倍交叉验证来评估准确性。这会将我们的数据集分为10个部分, 在9上训练, 在1上测试, 然后对训练测试拆分的所有组合重复。

# Test options and evaluation metric
seed = 7
scoring = 'accuracy'

"准确性"指标用于评估模型。它是正确预测的实例数除以数据集中实例总数再乘以100得出的百分比(例如, 准确度为95％)。

5.3建立模型

尚不知道哪种算法可以解决此问题或使用哪种配置。因此, 从图中得出的想法是, 某些类在某些维度上是部分线性可分离的。

评估6种不同的算法：

• 逻辑回归(LR)
• 线性判别分析(LDA)
• K最近邻居(KNN)。
• 分类和回归树(CART)。
• 高斯朴素贝叶斯(NB)。
• 支持向量机(SVM)。

选择的算法是线性(LR和LDA)和非线性(KNN, CART, NB和SVM)算法的混合。在每次运行之前重置随机数种子, 以确保使用完全相同的数据拆分执行每种算法的评估。它确保结果可直接比较。

建立和评估模型：

# Spot Check Algorithms
models = []
models.append(( 'LR' , LogisticRegression(solver = 'liblinear' , multi_class = 'ovr' )))
models.append(( 'LDA' , LinearDiscriminantAnalysis()))
models.append(( 'KNN' , KNeighborsClassifier()))
models.append(( 'CART' , DecisionTreeClassifier()))
models.append(( 'NB' , GaussianNB()))
models.append(( 'SVM' , SVC(gamma = 'auto' )))
  
# evaluate each model in turn
results = []
names = []
  
for name, model in models:
     kfold = model_selection.KFold(n_splits = 10 , random_state = seed)
     cv_results = model_selection.cross_val_score(
             model, X_train, Y_train, cv = kfold, scoring = scoring)
     results.append(cv_results)
     names.append(name)
     msg = "% s: % f (% f)" % (name, cv_results.mean(), cv_results.std())
     print (msg)

5.4选择最佳模型

比较模型并选择最准确的模型。运行上面的示例可获得以下原始结果：

LR: 0.966667 (0.040825)
LDA: 0.975000 (0.038188)
KNN: 0.983333 (0.033333)
CART: 0.975000 (0.038188)
NB: 0.975000 (0.053359)
SVM: 0.991667 (0.025000)

支持向量机(SVM)的估计准确性得分最高。

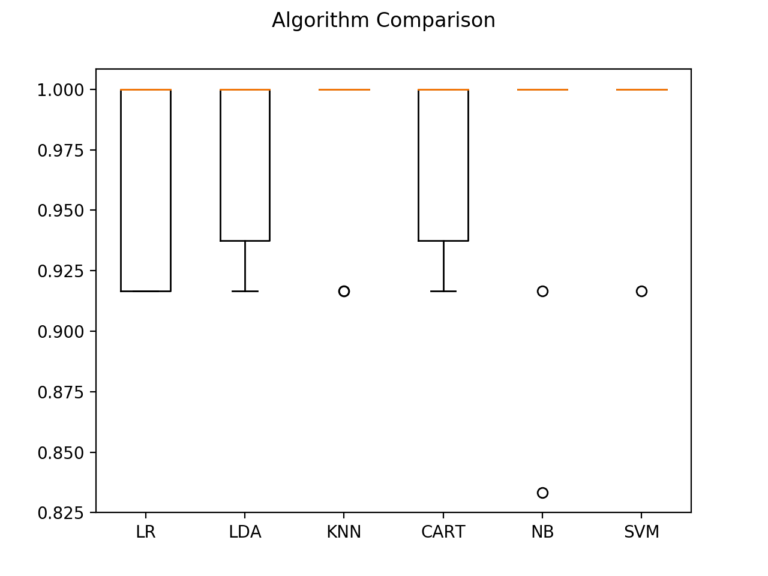
创建模型评估结果图, 并比较每个模型的分布和平均准确性。每种算法都有大量的精度度量, 因为每种算法都被评估了10次(10倍交叉验证)。

# Compare Algorithms
fig = plt.figure()
fig.suptitle( 'Algorithm Comparison' )
ax = fig.add_subplot( 111 )
plt.boxplot(results)
ax.set_xticklabels(names)
plt.show()

箱形图和晶须图被压缩在该范围的顶部, 许多样本达到了100％的精度。

6.做出预测

KNN算法非常简单, 并且是根据我们的测试得出的准确模型。

直接在验证集上运行KNN模型, 并将结果汇​​总为最终准确性得分, 混淆矩阵和分类报告。

# Make predictions on validation dataset
knn = KNeighborsClassifier()
knn.fit(X_train, Y_train)
predictions = knn.predict(X_validation)
print (accuracy_score(Y_validation, predictions))
print (confusion_matrix(Y_validation, predictions))
print (classification_report(Y_validation, predictions))

准确度为0.9或90％。混淆矩阵提供了三个错误的指示。最后, 分类报告按精度, 召回率, f1得分和支持分类显示了每个分类, 并显示了出色的结果(允许的验证数据集很小)。

0.9
[[ 7  0  0]
 [ 0 11  1]
 [ 0  2  9]]
                 precision    recall  f1-score   support

    Iris-setosa       1.00      1.00      1.00         7
Iris-versicolor       0.85      0.92      0.88        12
 Iris-virginica       0.90      0.82      0.86        11

      micro avg       0.90      0.90      0.90        30
      macro avg       0.92      0.91      0.91        30
   weighted avg       0.90      0.90      0.90        30

首先, 你的面试准备可通过以下方式增强你的数据结构概念：Python DS课程。

---