算法设计：如何解决2-可满足性（2-SAT）问题？

2021年3月21日17:21:27 发表评论 2,227 次浏览

本文概述

布尔可满足性问题

布尔可满足性或简单SAT考试是确定布尔公式是否可满足或无法满足的问题。

  • 满意的：如果可以为布尔变量分配值, 从而使公式变为TRUE, 则可以说该公式是可满足的。
  • 不满意的：如果不可能分配这样的值, 那么我们说该公式是不满足的。

例子：

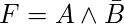
F = A \ wedge \ bar {B}

可以满足, 因为A = TRUE和B = FALSE使F = TRUE。

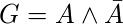
G = A \ wedge \ bar {A}

, 是不令人满意的, 因为：

true false false
false true false

注:布尔可满足性问题是np完全的(关于证明，参考库克定理 https://en.wikipedia.org/wiki/Cook%E2%80%93Levin_theorem)。

2-可满足性（2-SAT）问题1

什么是2-SAT问题

2-SAT是布尔可满足性问题的特例, 可以在多项式时间内求解。

为了更好地理解这一点, 首先让我们看看什么是合取范式(CNF)或也称为和积(POS)。

CNF：

CNF是子句的连接(AND), 其中每个子句都是析取(OR)。

现在, 2-SAT将SAT问题限制为仅将那些布尔表达式表示为CNF, 而每个子句仅具有2学期(也被称为2-CNF)。

例子：

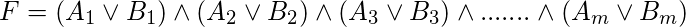
F =（A_1 \ vee B_1）\ wedge（A_2 \ vee B_2）\ wedge（A_3 \ vee B_3）\ wedge ....... \ wedge（A_m \ vee B_m）

因此, 2满足性问题可以表述为：

给定CNF, 每个子句只有2个项, 是否可以将这些值分配给变量, 以使CNF为TRUE？

例子：

Input : 
Output : The given expression is satisfiable. 
         (for x1 = FALSE, x2 = TRUE)

Input : 
Output : The given expression is unsatisfiable. 
         (for all possible combinations of x1 and x2)

推荐：请尝试以下方法{IDE}首先, 在继续解决方案之前。

2-SAT问题的方法

为了使CNF值变为TRUE, 每个子句的值都应为TRUE。让条款之一

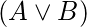
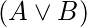
（A \ vee B）

.

（A \ vee B）

=真

如果A = 0, 则B必须为1, 即

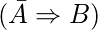
（\ bar {A} \ Rightarrow B）

如果B = 0, 则A必须为1, 即

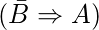
（\ bar {B} \ Rightarrow A）

从而, 

= TRUE is equivalent to

现在, 我们可以将CNF表示为蕴涵。因此, 我们为CNF的每个子句创建一个具有2条边的隐含图。

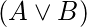
（A \ vee B）

在隐含图中表示为

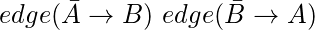
edge（\ bar {A} \ rightarrow B）\＆edge（\ bar {B} \ rightarrow A）

因此, 对于带有" m"子句的布尔公式, 我们制作一个具有以下含义的隐含图：

  • 每个子句2条边, 即" 2m"条边。
  • 布尔公式中涉及的每个布尔变量1个节点。

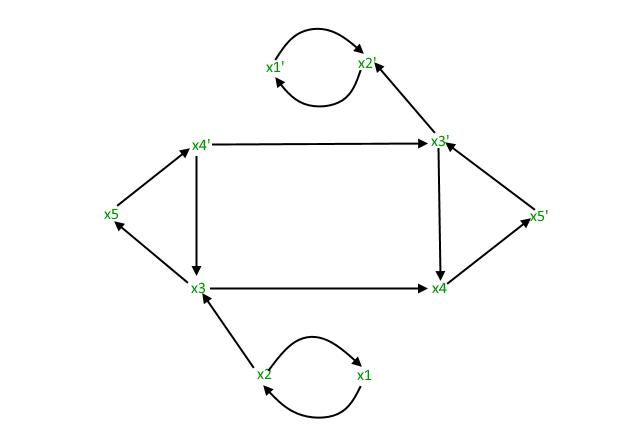
让我们看一个蕴涵图的例子。

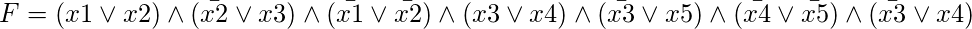
F =（x1 \ vee x2）\ wedge（\ bar {x2} \ vee x3）\ wedge（\ bar {x1} \ vee \ bar {x2}）\ wedge（x3 \ vee x4）\ wedge（\ bar { x3} \ vee x5）\ wedge（\ bar {x4} \ vee \ bar {x5}）\ wedge（\ bar {x3} \ vee x4）
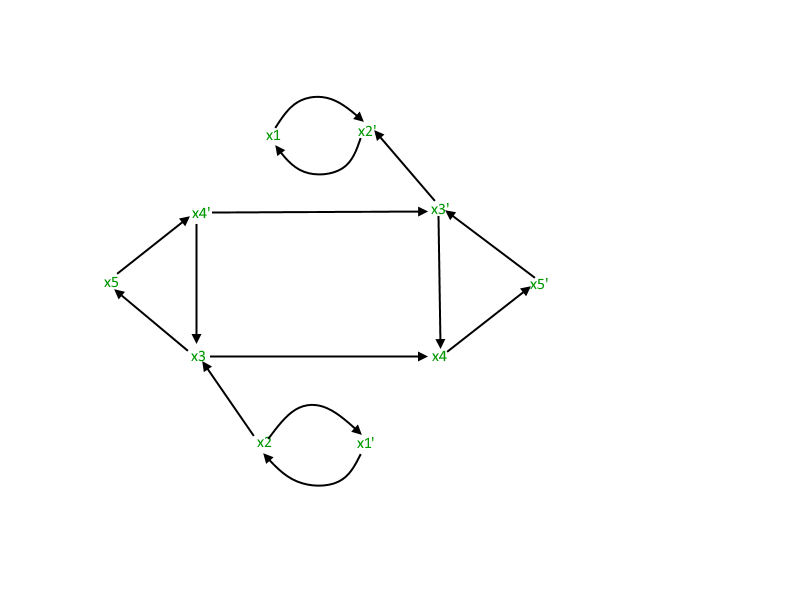
2-可满足性（2-SAT）问题2

注意：

含义(如果从A到B, 则等价)等于其对立的(如果从

\ bar {B}

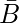
然后

\ bar {A}

)。

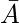
现在, 考虑以下情况：

CASE 1: If  exists in the graph
This means 
If X = TRUE, = TRUE, which is a contradiction.
But if X = FALSE, there are no implication constraints.
Thus, X = FALSE
CASE 2: If  exists in the graph
This means 
If  = TRUE, X = TRUE, which is a contradiction.
But if  = FALSE, there are no implication constraints.
Thus, = FALSE i.e. X = TRUE
CASE 3: If  both exist in the graph
One edge requires X to be TRUE and the other one requires X to be FALSE.
Thus, there is no possible assignment in such a case.

结论：

如果有两个变量

X

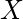
和

\ bar {X}

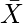
处于周期中

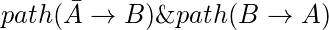
路径（\ bar {A} \ rightarrow B）\＆路径（{B} \ rightarrow A）

两者都存在, 那么CNF是无法满足的。否则, 可能存在分配并且CNF是可满足的。

请注意, 由于以下含义, 我们使用路径：

如果我们有

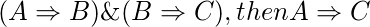
（A \ Rightarrow B）\＆（B \ Rightarrow C），然后是A \ Rightarrow C

因此, 如果我们在隐含图中有一条路径, 则与具有直接边几乎相同。

从实施观点出发的结论：

如果X和

\ bar {X}

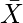
如果在同一SCC(牢固连接的组件)中, 则CNF不能令人满意。

有向图的强连接组件具有节点, 因此可以从该SCC中的每个其他节点访问每个节点。

现在, 如果X和

\ bar {X}

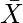
躺在同一SCC上, 我们肯定会

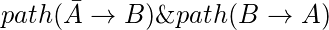
路径（\ bar {A} \ rightarrow B）\＆路径（{B} \ rightarrow A）

现在, 因此得出结论。

SCC的检查可以在O(E + V)中使用Kosaraju的算法

// C++ implementation to find if the given
// expression is satisfiable using the
// Kosaraju's Algorithm
#include <bits/stdc++.h>
using namespace std;
  
const int MAX = 100000;
  
// data structures used to implement Kosaraju's
// Algorithm. Please refer
vector< int > adj[MAX];
vector< int > adjInv[MAX];
bool visited[MAX];
bool visitedInv[MAX];
stack< int > s;
  
// this array will store the SCC that the
// particular node belongs to
int scc[MAX];
  
// counter maintains the number of the SCC
int counter = 1;
  
// adds edges to form the original graph
void addEdges( int a, int b)
{
     adj[a].push_back(b);
}
  
// add edges to form the inverse graph
void addEdgesInverse( int a, int b)
{
     adjInv[b].push_back(a);
}
  
// for STEP 1 of Kosaraju's Algorithm
void dfsFirst( int u)
{
     if (visited[u])
         return ;
  
     visited[u] = 1;
  
     for ( int i=0;i<adj[u].size();i++)
         dfsFirst(adj[u][i]);
  
     s.push(u);
}
  
// for STEP 2 of Kosaraju's Algorithm
void dfsSecond( int u)
{
     if (visitedInv[u])
         return ;
  
     visitedInv[u] = 1;
  
     for ( int i=0;i<adjInv[u].size();i++)
         dfsSecond(adjInv[u][i]);
  
     scc[u] = counter;
}
  
// function to check 2-Satisfiability
void is2Satisfiable( int n, int m, int a[], int b[])
{
     // adding edges to the graph
     for ( int i=0;i<m;i++)
     {
         // variable x is mapped to x
         // variable -x is mapped to n+x = n-(-x)
  
         // for a[i] or b[i], addEdges -a[i] -> b[i]
         // AND -b[i] -> a[i]
         if (a[i]>0 && b[i]>0)
         {
             addEdges(a[i]+n, b[i]);
             addEdgesInverse(a[i]+n, b[i]);
             addEdges(b[i]+n, a[i]);
             addEdgesInverse(b[i]+n, a[i]);
         }
  
         else if (a[i]>0 && b[i]<0)
         {
             addEdges(a[i]+n, n-b[i]);
             addEdgesInverse(a[i]+n, n-b[i]);
             addEdges(-b[i], a[i]);
             addEdgesInverse(-b[i], a[i]);
         }
  
         else if (a[i]<0 && b[i]>0)
         {
             addEdges(-a[i], b[i]);
             addEdgesInverse(-a[i], b[i]);
             addEdges(b[i]+n, n-a[i]);
             addEdgesInverse(b[i]+n, n-a[i]);
         }
  
         else
         {
             addEdges(-a[i], n-b[i]);
             addEdgesInverse(-a[i], n-b[i]);
             addEdges(-b[i], n-a[i]);
             addEdgesInverse(-b[i], n-a[i]);
         }
     }
  
     // STEP 1 of Kosaraju's Algorithm which
     // traverses the original graph
     for ( int i=1;i<=2*n;i++)
         if (!visited[i])
             dfsFirst(i);
  
     // STEP 2 pf Kosaraju's Algorithm which
     // traverses the inverse graph. After this, // array scc[] stores the corresponding value
     while (!s.empty())
     {
         int n = s.top();
         s.pop();
  
         if (!visitedInv[n])
         {
             dfsSecond(n);
             counter++;
         }
     }
  
     for ( int i=1;i<=n;i++)
     {
         // for any 2 vairable x and -x lie in
         // same SCC
         if (scc[i]==scc[i+n])
         {
             cout << "The given expression "
                  "is unsatisfiable." << endl;
             return ;
         }
     }
  
     // no such variables x and -x exist which lie
     // in same SCC
     cout << "The given expression is satisfiable."
          << endl;
     return ;
}
  
//  Driver function to test above functions
int main()
{
     // n is the number of variables
     // 2n is the total number of nodes
     // m is the number of clauses
     int n = 5, m = 7;
  
     // each clause is of the form a or b
     // for m clauses, we have a[m], b[m]
     // representing a[i] or b[i]
  
     // Note:
     // 1 <= x <= N for an uncomplemented variable x
     // -N <= x <= -1 for a complemented variable x
     // -x is the complement of a variable x
  
     // The CNF being handled is:
     // '+' implies 'OR' and '*' implies 'AND'
     // (x1+x2)*(x2’+x3)*(x1’+x2’)*(x3+x4)*(x3’+x5)*
     // (x4’+x5’)*(x3’+x4)
     int a[] = {1, -2, -1, 3, -3, -4, -3};
     int b[] = {2, 3, -2, 4, 5, -5, 4};
  
     // We have considered the same example for which
     // Implication Graph was made
     is2Satisfiable(n, m, a, b);
  
     return 0;
}

输出如下：

The given expression is satisfiable.

更多测试用例：

Input : n = 2, m = 3
        a[] = {1, 2, -1}
        b[] = {2, -1, -2}
Output : The given expression is satisfiable.

Input : n = 2, m = 4
        a[] = {1, -1, 1, -1}
        b[] = {2, 2, -2, -2}
Output : The given expression is unsatisfiable.

如果发现任何不正确的地方, 或者想分享有关上述主题的更多信息, 请写评论。

木子山

发表评论

:?: :razz: :sad: :evil: :!: :smile: :oops: :grin: :eek: :shock: :???: :cool: :lol: :mad: :twisted: :roll: :wink: :idea: :arrow: :neutral: :cry: :mrgreen: