计算机图形学中的2D转换算法实现|S1（对象缩放）

缩放变换会更改对象的大小。在缩放过程中, 我们压缩或扩展对象的尺寸。

缩放操作可以通过缩放因子sx和sy将多边形的每个顶点坐标(x, y)相乘得到变换后的坐标为(x '， y ')。

分别沿X和Y方向缩放对象。因此, 以上等式可以用矩阵形式表示：

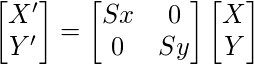
或P'= S.P

缩放过程：

注意：

如果缩放因子S小于1, 则我们减小对象的大小。如果比例因子S大于1, 则我们将增加对象的大小。

算法：

1. Make a 2x2 scaling matrix S as:
   Sx 0
   0  Sy
2. For each point of the polygon.
   (i) Make a 2x1 matrix P, where P[0][0] equals 
       to x coordinate of the point and P[1][0] 
       equals to y coordinate of the point.
   (ii) Multiply scaling matrix S with point 
        matrix P to get the new coordinate.
3. Draw the polygon using new coordinates.

下面是C的实现：

// C program to demonstrate scaling of abjects
#include<stdio.h>
#include<graphics.h>
  
// Matrix Multiplication to find new Coordinates.
// s[][] is scaling matrix. p[][] is to store
// points that needs to be scaled.
// p[0][0] is x coordinate of point.
// p[1][0] is y coordinate of given point.
void findNewCoordinate( int s[][2], int p[][1])
{
     int temp[2][1] = { 0 };
  
     for ( int i = 0; i < 2; i++)
         for ( int j = 0; j < 1; j++)
             for ( int k = 0; k < 2; k++)
                 temp[i][j] += (s[i][k] * p[k][j]);
  
     p[0][0] = temp[0][0];
     p[1][0] = temp[1][0];
}
  
// Scaling the Polygon
void scale( int x[], int y[], int sx, int sy)
{
     // Triangle before Scaling
     line(x[0], y[0], x[1], y[1]);
     line(x[1], y[1], x[2], y[2]);
     line(x[2], y[2], x[0], y[0]);
  
     // Initializing the Scaling Matrix.
     int s[2][2] = { sx, 0, 0, sy };
     int p[2][1];
  
     // Scaling the triangle
     for ( int i = 0; i < 3; i++)
     {
         p[0][0] = x[i];
         p[1][0] = y[i];
  
         findNewCoordinate(s, p);
  
         x[i] = p[0][0];
         y[i] = p[1][0];
     }
  
     // Triangle after Scaling
     line(x[0], y[0], x[1], y[1]);
     line(x[1], y[1], x[2], y[2]);
     line(x[2], y[2], x[0], y[0]);
}
  
// Driven Program
int main()
{
     int x[] = { 100, 200, 300 };
     int y[] = { 200, 100, 200 };
     int sx = 2, sy = 2;
  
     int gd, gm;
     detectgraph(&gd, &gm);
     initgraph(&gd, &gm, " " );
  
     scale(x, y, sx, sy);
     getch();
  
     return 0;
}

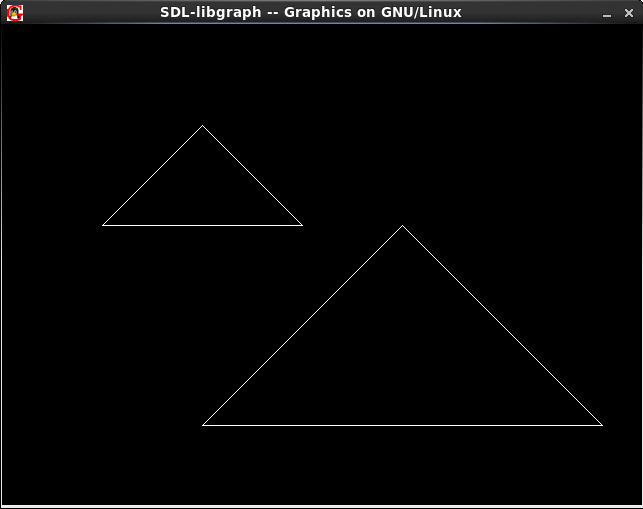
输出如下：

如果发现任何不正确的地方, 或者想分享有关上述主题的更多信息, 请写评论。